Бинарно стабло нити
Дефиниција бинарног стабла нити гласи:
"Бинарно стабло претраге зовемо Бинарно стабло нити ако сваки показивач на десно дете који би иначе био NULL показује на следбеника датог чвора, а сваки показивач на лево дете који би иначе био NULL показује на претходника датог чвора."[1]
Бинарно стабло нити омогућује обилазак чворова у бинарном стаблу линеарном путањом која је краћа него рекурзивни обилазак. Такође је могуће открити родитеља чвора у бинарном стаблу нити, без употреба показивача на родитеља или стека. То може бити корисно када је величина стека ограничена, или када су показивачи на родитеља недоступни (при тражењу родитеља коришћењем претраге у дубину).
Да би се видело како је ово могуће, узме се у обзир чвор k који има десно дете r. Тада леви показивач од r мора или показивати ка детету или назад према k. У случају да r има лево дете, то дете мора или имати лево дете или имати показивач према k, и тако даље за свако наредно лево дете. То значи да пратећи ланац левих показивача из r, у једном тренутку наилазим на показивач који води назад до k. Имамо симетричну ситуацију ако је q лево дете од p, тада пратимо десну децу од q , док не дођемо до показивача који води назад до p.
Типови бинарних стабала нити
[уреди | уреди извор]- Бинарних стабла са једноструким нитима: сваки чвор има нити или ка претходнику или ка следбенику.
- Бинарних стабла са двоструким нитима: сваки чвор има нити и ка претходнику и ка следбенику.
У Пајтону:
def parent(node):
if node is node.tree.root:
return None
else:
x = node
y = node
while True:
if is_thread(y.right):
p = y.right
if p is None or p.left is not node:
p = x
while not is_thread(p.left):
p = p.left
p = p.left
return p
elif is_thread(x.left):
p = x.left
if p is None or p.right is not node:
p = y
while not is_thread(p.right):
p = p.right
p = p.right
return p
x = x.left
y = y.right
Инордер обилазак
[уреди | уреди извор]Нити су везе до претходника и следбеника судећи по инордер обиласку.
Инордер обилазак стабла је ABCDEFGHI, претходник од E је D, а следбеник од E је F.
Пример
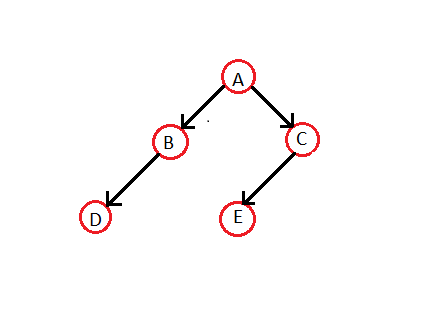
[уреди | уреди извор]Поступак формирања стабла нити од обичног бинарног стабла:
Инордер обилазак датог стабла је D B A E C. Из тога следи да ће одговарајуће бинарно стабло нити бити:
Нерекурзивни инордер обилазак бинарног стабла нити
[уреди | уреди извор]Пошто је ово нерекурзивна метода обиласка, она мора имати итеративну процедуру; што значи, сваки корак у обиласку чвора мора бити у петљи да би се исти применио за сваки чвор у стаблу. Посматраћемо инордер обилазак. У том случају, за сваки чвор, посетићемо лево подстабло (ако оно постоји) прво (ако га нисмо посетили раније); онда ћемо посетити (у нашем случају исписати његову вредност) самог чвора и на крају десно подстабло (ако оно постоји). Ако десно подстабло не постоји, проверавамо да ли постоји нит ка неком чвору и ако постоји онда разматрамо тај чвор. Следећи пример илуструје дати алгоритам.
Алгоритам
[уреди | уреди извор]Корак-1: За тренутни чвор проверити да ли има лево дете које се не налази на листи посећених. Ако има прелази се на корак-2, иначе на корак-3.
Корак-2: То лево дете се додаје на листу посећених чворова и узима се за даље разматрање. Прелази се на корак-6.
Корак-3: За тренутни чвор се провери да ли има десно дете. Ако има, прелази се на корак-4, иначе на корак-5.
Корак-4: То десно дете се узима за даље разматрање. Прелази се на корак-6.
Корак-5: Проверава се да ли постоји нит ка неком чвору и ако постоји онда се разматра тај чвор.
Корак-6: Прелази се на корак-1 ако нису сви чворови обиђени, иначе крај.
| Li | ||||
|---|---|---|---|---|
| Корак-1 | 'A' има лево дете B, које није посећено. Зато, смештамо B у „листу посећених чворова“ и B се даље разматра. | B | ||
| Корак-2 | 'B' такође има лево дете, 'D', које није на листи посећених чворова. Зато, смештамо 'D' у ту листу и даље га разматрамо. | B D | ||
| Корак-3 | 'D' нема лево дете, па исписујемо 'D'. Онда проверавамо да ли има десно дете. 'D' нема десно дете па онда тражимо нит која иде из њега. Нит иде ка 'B'. Зато, даље разматрамо 'B'. | B D | D | |
| Корак-4 | 'B' свакако има лево дете али се оно већ налази на листи посећених чворова. Зато, исписујемо 'B'. Онда тражимо његово десно дете али оно не постоји. Зато, даље разматрамо 'A' јер према њему иде нит. | B D | D B | |
| Корак-5 | 'A' има лево дете, 'B', али оно је већ на листи посећених чворова. Зато, исписујемо 'A'. Проверамо да ли има десно дете. 'A' има десно дете, 'C' које није на листи посећених чворова. Зато, додајемо га на ту листу и даље га разматрамо. | B D C | D B A | |
| Корак-6 | 'C' има лево дете 'E' које није на листи посећених чворова. Зато га додајемо на ту листу и даље разматрамо. | B D C E | D B A | |
| Корак-7 | и коначно..... | D B A E C |
Референце
[уреди | уреди извор]- ^ Van Wyk, Christopher J (1988). Data Structures and C Programs. Addison-Wesley. стр. 175. ISBN 978-0-201-16116-8.