И-Или дрво

И-или дрво је графички приказ смањења проблема (или циљева) до конјункције и дисјункције од под-проблем (или под-циљеви).

Пример

[уреди | уреди извор]

И-или дрво:

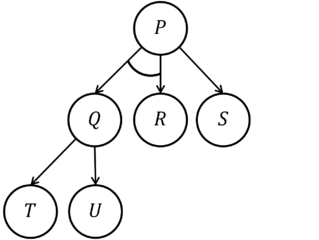
представља претрагу простора за решавање проблема P, користећи методе циљ-смањења:

P if Q and R
P if S
Q if T
Q if U

Дефиниције

[уреди | уреди извор]

Имајући у виду почетни проблем P0 и сет методе решавања проблема у облику:

P if P1 and … and Pn

повезани и-или дрво је скуп обележених чворова који су:

  1. Корен стабла је означен по чвору P0.
  2. За сваки чвор N ознаком од проблема или под-проблема P и за сваку методу обрасца P if P1 and … and Pn, постоји скуп деце чворови N1, …, Nn чвора N, тако да је сваки чвор Ni обележен са Pi. Чворови су спојене по луку, да би се разликовали од синова N који би могли бити повезани са другим методама.

Чвор N, обележен од проблема P,је успех чвора ако постоји метод обрасца P ако ништа (тј., P је „чињеница"). Чвор је неуспех чвора ако не постоји метод за решавање P.

Ако сва деца неког чвора N, спојене од истог лука, су успех чворови, онда чвор N је такође успех чвор. Иначе чвор је чвор неуспех.

Претраживање стратегије

[уреди | уреди извор]

И-или дрво одређује само претрагу простора за решавање проблема. Различите стратегије за претрагу за претраживање простор су могуће. Ово укључује претраживање стабла дубине прво, ширина-први или најбољи-први користећи неку меру пожељности решења. Стратегија претраживање може бити секвенцијална, тражење или генерисање један чвор у време, или паралелно, или у потрази генерисање неколико чворова паралелно.

Однос са логичким програмирањем

[уреди | уреди извор]

Методе које се користе за генерисање и-или дрвећа исказна логика програма (без променљивих). У случају логичких програма који садрже променљиве, раствори обједињени под-проблеми морају бити компатибилни. Предмет ове компликације, секвенцијална и паралелна стратегија за и-или дрвеће претраге обезбеђује компјутерски модел за извршавање логичких програма.

Однос са два играча игара

[уреди | уреди извор]

И-или дрвеће се такође може користити да представљају просторе претраге за две особе игара. Корен чвора таквог дрвета представља проблем једног од играча победничких игара, почевши од почетног стања игре. С обзиром чвор N, обележени од проблема P од победе играча из одређене државе, постоји један сет синтетичке деце чворова, који одговарају свим противниковим анкетираних потеза. За сваки од ових чворова деце, постоји низ од не-синтетичке деце чворова, који одговара свим бранећим потезима играча.

За решавање игре са дрвећа претрага броја доказа фамилија алгоритама, игра дрвећа да се мапира и / или дрвеће. MAX-чворова (тј. максимално играча да се пресели) су представљени као чворови ИЛИ, МIN-чворови карта до И чворова. Мапирање је могуће, када претраживање врши само са бинарним циљом, који обично „играч за кретање побеђује у игри“.

Литература

[уреди | уреди извор]