BLAKE (хеш-функція)

BLAKE — криптографічна хеш-функція, в розробці якої брали участь Жан-Філіп Омассон (Jean-Philippe Aumasson), Лука Хенцен (Luca Henzen), Віллі Майєр (Willi Meier), Рафаель Фан (Raphael C.-W. Phan).

Існують два варіанти хеш-функції: BLAKE-256 і BLAKE-512.

Історія

Вперше BLAKE була представлена на конкурсі криптографічних алгоритмів, який проводився Національним інститутом стандартів і технологій США BLAKE стала одним з п'яти фіналістів конкурсу.

Криптостійкість

Хеш-функція BLAKE побудована з трьох раніше вивчених компонентів:

• режим ітерації HAIFA забезпечує стійкість до атак другого роду
• внутрішня структура local wide-pipe забезпечує захист від колізій
• алгоритм стиснення для BLAKE є модифікованою версією потокового шифру ChaCha, який дуже добре розпаралелюється і чия безпека ретельно проаналізована^[1]

Швидкодія і реалізація

Швидкодія на двох різних процесорах:

Процесор	Швидкість (тактів/байт)
	BLAKE-256	BLAKE-512
Intel Core i5-2400M (Sandy Bridge)	7.49	5.64
AMD FX-8120 (Bulldozer)	11.83	6.88

Можливість реалізації на різних мікроконтролерах:

Мікроконтролер	BLAKE-256		BLAKE-512
	RAM(байт)	ROM(байт)	RAM(байт)	ROM(байт)
Cortex-M3 based microcontroller (32-bit processor)	280	1320	516	1776
ATmega1284P microcontroller (8-bit processor)	267	3434	525	6350

Швидкодія на FPGA: На FPGA Xilinx Virtex 5, BLAKE-256 реалізується на 56 комірках і може досягати пропускної здатності більш ніж в 160 Мбіт/с, а BLAKE-512 — на 108 комірках зі швидкістю до 270 Мбіт/с.

Швидкодія на ASIC: На 180 nm ASIC, BLAKE-256 може бути реалізована на 13.5 kGE. На 90 nm ASIC, BLAKE-256 реалізована на 38 kGE і може досягати продуктивності в 10 Гбіт/с, а BLAKE-512 — на 79 kGE і зі швидкістю 15 Гбіт/с^[2].

Алгоритм

Розглянемо алгоритм BLAKE-256^[3]

BLAKE-256 оперує з 32-бітними словами і повертає 32-байтний хеш.

Константи

Існують початкові константи, т.н. INITIAL VALUES (IV):

IV0 = 6A09E667 IV1 = BB67AE85
IV2 = 3C6EF372 IV3 = A54FF53A
IV4 = 510E527F IV5 = 9B05688C
IV6 = 1F83D9AB IV7 = 5BE0CD19

16 констант (Перші цифри числа пі):

c0  = 243F6A88 c1  = 85A308D3
c2  = 13198A2E c3  = 03707344
c4  = A4093822 c5  = 299F31D0
c6  = 082EFA98 c7  = EC4E6C89
c8  = 452821E6 c9  = 38D01377
c10 = BE5466CF c11 = 34E90C6C
c12 = C0AC29B7 c13 = C97C50DD
c14 = 3F84D5B5 c15 = B5470917 

перестановки {0,…,15} (використовуються у всіх функціях BLAKE):

σ0 = 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
σ1 = 14 10 4 8 9 15 13 6 1 12 0 2 11 7 5 3
σ2 = 11 8 12 0 5 2 15 13 10 14 3 6 7 1 9 4
σ3 = 7 9 3 1 13 12 11 14 2 6 5 10 4 0 15 8
σ4 = 9 0 5 7 2 4 10 15 14 1 11 12 6 8 3 13
σ5 = 2 12 6 10 0 11 8 3 4 13 7 5 15 14 1 9
σ6 = 12 5 1 15 14 13 4 10 0 7 6 3 9 2 8 11
σ7 = 13 11 7 14 12 1 3 9 5 0 15 4 8 6 2 10
σ8 = 6 15 14 9 11 3 0 8 12 2 13 7 1 4 10 5
σ9 = 10 2 8 4 7 6 1 5 15 11 9 14 3 12 13 0

Функції стиснення

Функція стиснення алгоритму BLAKE-256 приймає на вхід:

• Змінні ланцюжка h = h₀,…,h₇ (8 слів);
• Блок повідомлення m = m₀,…,m₁₅;
• Значення солі s = s₀,…,s₃;
• Значення лічильника t = t₀,t₁.

Таким чином, на вхід їй подається 30 слів (8+16+4+2=30, 30*4 = 120 байт = 960 біт). Повертає функція стиснення тільки нове значення змінних ланцюжка: h' = h'₀,…,h'₇. Надалі будемо позначати h'=compress(h, m, s, t)>

Ініціалізація

16 змінних, v₀,…,v₁₅, що описують поточний стан v, ініціалізуються початковими значеннями в залежності від вхідних даних і представлені у вигляді матриці 4×4:

${\displaystyle {\begin{pmatrix}v_{0}&v_{1}&v_{2}&v_{3}\\v_{4}&v_{5}&v_{6}&v_{7}\\v_{8}&v_{9}&v_{10}&v_{11}\\v_{12}&v_{13}&v_{14}&v_{15}\\\end{pmatrix}}}$←${\displaystyle {\begin{pmatrix}h_{0}&h_{1}&h_{2}&h_{3}\\h_{4}&h_{5}&h_{6}&h_{7}\\s_{0}\oplus c_{0}&s_{1}\oplus c_{1}&s_{2}\oplus c_{2}&s_{3}\oplus c_{3}\\t_{0}\oplus c_{4}&t_{0}\oplus c_{5}&t_{1}\oplus c_{6}&t_{1}\oplus c_{7}\\\end{pmatrix}}}$

Раундова функція

Після того, як стан v ініціалізований, запускається серія з 14 раундів. Раунд — це операція над станом ${\displaystyle v}$, яка виробляє обчислення, розбиті на наступні блоки:

G0(v0, v4, v8 , v12) G1(v1, v5, v9 , v13) G2(v2, v6, v10, v14) G3(v3, v7, v11, v15) 
G4(v0, v5, v10, v15) G5(v1, v6, v11, v12) G6(v2, v7, v8 , v13) G7(v3, v4, v9 , v14) 

на r-му раунді блок обчислень ${\displaystyle G_{i}(a,b,c,d)}$ працює наступним чином:

Графічна ілюстрація роботи блоку обчислень Gi

j ← σr%10[2×i]
k ← σr%10[2×i+1]
a ← a + b + (mj ⊕ ck) 
d ← (d ⊕ a) >>> 16
c ← c + d 
b ← (b ⊕ c) >>> 12
a ← a + b + (mk ⊕ cj) 
d ← (d ⊕ a) >>> 8
c ← c + d 
b ← (b ⊕ c) >>> 7

Вертикальній(column) і діагональний(diagonal) кроки алгоритму BLAKE-256 

Перші чотири блоки G₀,…,G₃ можуть обчислюватися паралельно, так як кожен змінює свою певну колонку змінних матриці станів. Назвемо процедуру обчислення G₀,…,G₃ column step. Точно також можуть бути паралельно обчислені G₄,…,G₇, але вони в свою чергу змінюють кожен свою діагональ матриці стану v. Тому назвемо процедуру обчислення G₄,…,G₇ diagonal step. Можливість паралельного обчислення G_i представлена графічно.

На раундах, номери r яких більше 9, використовується перестановка σ_r%10, наприклад, на 13-тому раунді використовується σ₃.

Останній крок

Після всіх раундів нове значення змінних ланцюжка h'₀,…,h'₇ обчислюється із змінних ${\displaystyle v_{0},...,v_{15}}$ матриці стану, вхідних змінних ${\displaystyle h}$ і з солі ${\displaystyle s}$:

h'0 ← h0 ⊕ s0 ⊕ v8
h'1 ← h1 ⊕ s1 ⊕ v9
h'2 ← h2 ⊕ s2 ⊕ v10
h'3 ← h3 ⊕ s3 ⊕ v11
h'4 ← h4 ⊕ s4 ⊕ v12
h'5 ← h5 ⊕ s5 ⊕ v13
h'6 ← h6 ⊕ s6 ⊕ v14
h'7 ← h7 ⊕ s7 ⊕ v15

Хешування повідомлення

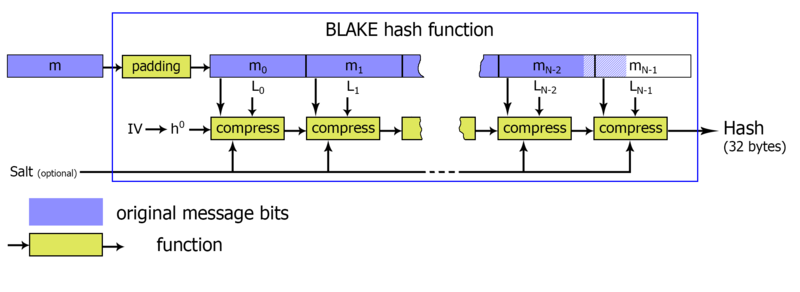
Опишемо процес хешування повідомлення m довжиною l<2^64 біт. Спочатку повідомлення доповнюється функцією padding даними для кратності 512 біт (64 байтам), потім, блок за блоком, його обробляє функція стиснення compression function.

У функції padding повідомлення спочатку доповнюється бітами, так, що його довжина стає по модулю 512 дорівнює 447: спочатку додається 1, потім необхідну кількість нулів. Після цього додається ще одна одиниця і 64-бітове представлення довжини повідомлення l від старшого до молодшого біта. Таким чином, довжина повідомлення стає кратною 512. Padding гарантує, що довжина повідомлення стане кратною 512 бітам.

Щоб вирахувати хеш повідомлення, результат функції padding ділиться на блоки з 16 слів m₀,…,m_N-1. Нехай L_i — кількість біт вихідного повідомлення у блоках m₀,…,m_i, тобто виключаючи ті біти, які були додані в процедурі padding. Наприклад, якщо повідомлення має довжину 600 біт, то після процедури padding воно буде мати 1024 біт і буде розділено на два блоки: m₀ і m₁. Притому L₀=512, L₁=600.

В деяких випадках останній блок не містить біт оригінального повідомлення. Наприклад, якщо у вихідному повідомленні 1020 біт, то в результаті процедури padding воно буде мати довжину 1536 біт і в m₀ буде 512 біт вихідного повідомлення m₁ — 508, а в m₂ — 0. Виставимо L₀=512, L₁=1020, а L₂=0. Тобто правило таке: якщо в останньому блоці немає біт оригінального повідомлення, то виставимо лічильник L_N-1 рівним 0. Це гарантує, що якщо i ≠ j, то L_i ≠ L_j. Значення солі визначається користувачем або задається рівним 0, якщо її не потрібно використовувати (s₀=s₁=s₂=s₃=0). Хеш повідомлення таким чином обчислюється:

h0 ← IV
for i=0,...,N-1
 hi+1 ← compress(hi,mi,s,li)
return hN.

Процес хешування наочно представлений на блок-схемі:

Алгоритм 64-бітної версії функції ідентичний: значення зсуву рівні 32, 25, 16 і 11 відповідно, число раундів збільшено до 16.

Відмінності від quarterround алгоритму ChaCha

• Додавання констант повідомлення.
• Змінений напрямок зсуву.

Хеші BLAKE

BLAKE-512("")
 = A8CFBBD73726062DF0C6864DDA65DEFE58EF0CC52A5625090FA17601E1EECD1B
 628E94F396AE402A00ACC9EAB77B4D4C2E852AAAA25A636D80AF3FC7913EF5B8

BLAKE-512("The quick brown fox jumps over the lazy dog")
 = 1F7E26F63B6AD25A0896FD978FD050A1766391D2FD0471A77AFB975E5034B7AD
 2D9CCF8DFB47ABBBE656E1B82FBC634BA42CE186E8DC5E1CE09A885D41F43451

BLAKE2

BLAKE2 (Сайт BLAKE2 [Архівовано 1 листопада 2018 у Wayback Machine.]) — це поліпшена версія BLAKE — одного з п'яти фіналістів конкурсу на хеш-функції SHA-3 (головним чином покращено швидкодію), представлена 21 грудня 2012 року. Розробники: Jean-Philippe Aumasson, Samuel Neves, Zooko Wilcox-O Hearn, і Christian Winnerlein. Була створена як альтернатива широко використовуваним в минулому MD5 і SHA-1, в яких були знайдені уразливості.

Відмінності від BLAKE

У BLAKE2, на відміну від BLAKE, немає додавання констант в раундовій функції. Також змінено константи зсуву, спрощено додавання, доданий блок параметрів, який складається з ініціалізуючими векторами. Крім того, скорочено кількість раундів з 16 до 12 у функції BLAKE2b (аналог BLAKE-512) і з 14 до 10 у BLAKE2s (аналог BLAKE-256). В результаті число тактів на біт скоротилася з 7,49 для BLAKE-256 і 5,64 для BLAKE-512 до 5,34 і 3,32 для Blake2s і Blake2b відповідно.

Хеші BLAKE2

BLAKE2b-512("")
 = 786A02F742015903C6C6FD852552D272912F4740E15847618A86E217F71F5419
 D25E1031AFEE585313896444934EB04B903A685B1448B755D56F701AFE9BE2CE

BLAKE2b-512("The quick brown fox jumps over the lazy dog")
 = A8ADD4BDDDFD93E4877D2746E62817B116364A1FA7BC148D95090BC7333B3673
 F82401CF7AA2E4CB1ECD90296E3F14CB5413F8ED77BE73045B13914CDCD6A918

BLAKE2s-256("")


= 69217A3079908094E11121D042354A7C1F55B6482CA1A51E1B250DFD1ED0EEF9





BLAKE2s-256("The quick brown fox jumps over the lazy dog")


= 606BEEEC743CCBEFF6CBCDF5D5302AA855C256C29B88C8ED331EA1A6BF3C8812





BLAKE2s-128("")


= 64550D6FFE2C0A01A14ABA1EADE0200C





BLAKE2s-128("The quick brown fox jumps over the lazy dog")


= 96FD07258925748A0D2FB1C8A1167A73

Джерела

1. Документація BLAKE на офіційному сайті [Архівовано 9 грудня 2017 у Wayback Machine.], стор 3 Introduction.
2. Офіційний сайт BLAKE. Архів оригіналу за 16 квітня 2018. Процитовано 16 квітня 2018.
3. Документація BLAKE на офіційному сайті [Архівовано 9 грудня 2017 у Wayback Machine.], ст.8 Specification.

Література

Eli Biham and Orr Dunkelman. A framework for iterative hash functions - HAIFA. — ePrint, 2007. — 207 с.

Посилання

• Сайт BLAKE [Архівовано 29 жовтня 2018 у Wayback Machine.]
• Сайт BLAKE2 [Архівовано 1 листопада 2018 у Wayback Machine.]
• Вихідний код на VHDL, розроблений Групою Дослідників в Області Криптографії університету Джорджа Мейсона [Архівовано 25 квітня 2012 у Wayback Machine.]