Коефіцієнт локального відхилення
| Частина з циклу |
| Машинне навчання та добування даних |
|---|
 |
Коефіцієнт локального видхилення (КЛВ, англ. local outlier factor) — це алгоритм для виявлення аномалій. Він був запропонований Маркусом М. Бройнігом, Гансом-Пітером Крігелем[en], Раймондом Т. Нґом і Йоргом Сандером у 2000 році для пошуку аномальних точок даних шляхом вимірювання локального відхилення даної точки даних по відношенню до сусідніх точок[1].
КЛВ використовує деякі поняття з алгоритмів DBSCAN і OPTICS, наприклад поняття «відстань до ядра» і «відстань доступності», які використовуються для оцінки локальної щільності[2].

Коефіцієнт локального відхилення базується на концепції локальної щільності, де локальність визначається k найближчими сусідами, відстань до яких використовується для оцінки щільності. Порівнюючи локальну щільність об'єкта з локальною щільністю його сусідів, можна ідентифікувати області з подібною щільністю та точки, які мають значно нижчу щільність, ніж їхні сусіди. Такі точки вважаються викидами.
Локальна щільність оцінюється за допомогою типової відстані, на якій можна «дотягнутися» до точки від її сусідів. Визначення «відстані досяжності», що використовується в КЛВ, є додатковим заходом для отримання більш стабільних результатів у кластерах. «Відстань досяжності», яку використовує КЛВ, має деякі нюанси, які часто виявляються спотвореними у вторинних джерелах, наприклад, у підручнику Етема Алпайдіна[3].
Нехай k-distance(A) визначається як відстань об'єкта A до k-го найближчого сусіда. Зауважте, що множина k найближчих сусідів включає всі об'єкти на цій відстані, яких у випадку «рівності» можуть бути більше, ніж k об'єктів. Позначимо множину k найближчих сусідів як Nk(A).

Ця відстань використовується для визначення того, що називається відстанню досяжності (reachability distance):
Тобто, відстань досяжності об'єкта A від B є справжньою відстанню двох об'єктів, і є, щонайменше, k-відстанню від B. Об'єкти, які належать до k найближчих сусідів B («ядро» B, див. кластерний аналіз DBSCAN), вважаються однаково віддаленими. Причиною цього є зменшення статистичних флуктуацій між усіма точками A поблизу B, де збільшення значення k збільшує ефект згладжування[1]. Зауважте, що це не відстань у математичному визначенні, оскільки вона не є симетричною. (Хоча завжди використовувати k-distance(A) є поширеною помилкою[4], це дає дещо інший метод, — спрощений-КЛВ[4]).
Локальна щільність досяжності об'єкта A визначається за допомогою
- ,
яка є оберненою до середньої відстані досяжності об'єкта А від його сусідів. Зауважте, що це не середня досяжність сусідів з A (яка за визначенням була б k-distance(A)), а відстань, на якій точка A може бути «досяжною» від своїх сусідів. У випадку дублювання точок, це значення може стати нескінченністю.
Потім локальна щільність досяжності порівнюється з щільністю сусідів, які використовують
це середня локальна щільність досяжності сусідів, поділена на власну локальну щільність досяжності об'єкта. Значення, що дорівнює приблизно 1 вказує на те, що об'єкт можна порівняти зі своїми сусідами (і, таким чином, не є викидом). Значення нижче 1 вказує на більш щільну область (що вказує на нормальну точку), тоді як значення, значно більші за 1, вказують на викиди.
LOF(k) ~ 1 означає: Така ж щільність, як у сусідів,
LOF(k) < 1 означає: Вища щільність, ніж у сусідів (нормально точка),
LOF(k) > 1 означає: Нижча щільність, ніж у сусідів (викид).
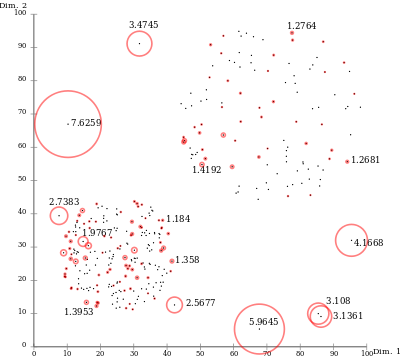
Завдяки локальному підходу КЛВ може ідентифікувати викиди в наборі даних, які не були б викидами в іншій ділянці набору даних. Наприклад, точка на «малій» відстані до дуже щільного кластера є викидом, тоді як точка в розрідженому кластері може демонструвати подібні відстані до своїх сусідів.
Хоча геометрична інтуїція КЛВ застосовна лише до векторних просторів низької розмірності, алгоритм можна застосовувати в будь-якому контексті, де можна визначити функцію неподібності. Експериментально було показано, що він дуже добре працює у багатьох застосунках, часто перевершуючи конкурентів, наприклад, у виявленні вторгнень у мережу[5] та на оброблених даних еталонного тесту класифікації[6].
Сімейство методів КЛВ можна легко узагальнити, а потім застосувати до різних інших задач, таких як виявлення викидів у географічних даних, відеопотоках або мережах авторства[4].
Отримані значення є частками, і їх важко інтерпретувати. Значення 1 або навіть менше вказує на явне нормальне значення, але немає чіткого правила, коли точка є викидом. В одному наборі даних значення 1,1 уже може бути викидом, в іншому наборі даних і параметризації (із сильними локальними коливаннями) значення 2 все ще може бути викидом. Ці відмінності також можуть виникати всередині набору даних через локальність методу. Існують розширення КЛВ, які намагаються покращити КЛВ у таких аспектах:
- Feature Bagging for Outlier Detection[7] запускає КЛВ на кількох проекціях і поєднує результати для покращення якості виявлення для багатовимірних даних. Це перший підхід ансамблевого навчання до виявлення викидів, інші варіанти див[8].
- Local Outlier Probability (LoOP)[9] — це метод похідний від КЛВ, але з використанням недорогої локальної статистики, щоб бути менш чутливим до вибору параметра k . Також, отримані значення масштабуються до діапазону значень [0:1] .
- Interpreting and Unifying Outlier Scores[10] пропонує нормалізацію показників КЛВ до інтервалу [0:1] за допомогою статистичного масштабування для підвищення зручності використання, і цей підхід можна розглядати, як вдосконалену версію ідей LoOP.
- У статті On Evaluation of Outlier Rankings and Outlier Scores[11] пропонуються методи вимірювання подібності та різноманітності методів для побудови вдосконалених ансамблів виявлення викидів з використанням варіантів КЛВ та інших алгоритмів і вдосконалення підходу Feature Bagging, описаного вище.
- У статті Local outlier detection reconsidered: a generalized view on locality with applications to spatial, video, and network outlier detection[4] обговорюється загальна схема в різних методах виявлення локальних викидів (включаючи, наприклад, КЛВ, спрощену версію КЛВ і LoOP), що дозволяє абстрагуватися та виокремити загальну структуру. Ця структура потім застосовується, наприклад, для виявлення викидів у географічних даних, відеопотоках і мережах авторства.
- ↑ а б Breunig, M. M.; Kriegel, H.-P.; Ng, R. T.; Sander, J. (2000). LOF: Identifying Density-based Local Outliers (PDF). Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. SIGMOD. с. 93—104. doi:10.1145/335191.335388. ISBN 1-58113-217-4.
- ↑ Breunig, M. M.; Kriegel, H.-P.; Ng, R. T.; Sander, J. R. (1999). OPTICS-OF: Identifying Local Outliers. Principles of Data Mining and Knowledge Discovery. Lecture Notes in Computer Science. Т. 1704. с. 262. doi:10.1007/978-3-540-48247-5_28. ISBN 978-3-540-66490-1.
- ↑ Alpaydin, Ethem (2020). Introduction to machine learning (вид. Fourth). Cambridge, Massachusetts. ISBN 978-0-262-04379-3. OCLC 1108782604.
- ↑ а б в г Schubert, E.; Zimek, A.; Kriegel, H. -P. (2012). Local outlier detection reconsidered: A generalized view on locality with applications to spatial, video, and network outlier detection. Data Mining and Knowledge Discovery. 28: 190—237. doi:10.1007/s10618-012-0300-z.
- ↑ Lazarevic, A.; Ozgur, A.; Ertoz, L.; Srivastava, J.; Kumar, V. (2003). A comparative study of anomaly detection schemes in network intrusion detection (PDF). Proc. 3rd SIAM International Conference on Data Mining: 25—36. Архів оригіналу (PDF) за 17 липня 2013. Процитовано 14 травня 2010.
- ↑ Campos, Guilherme O.; Zimek, Arthur; Sander, Jörg; Campello, Ricardo J. G. B.; Micenková, Barbora; Schubert, Erich; Assent, Ira; Houle, Michael E. (2016). On the evaluation of unsupervised outlier detection: measures, datasets, and an empirical study. Data Mining and Knowledge Discovery. 30 (4): 891—927. doi:10.1007/s10618-015-0444-8. ISSN 1384-5810.
- ↑ Lazarevic, A.; Kumar, V. (2005). Feature bagging for outlier detection. Proc. 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining: 157—166. doi:10.1145/1081870.1081891. ISBN 159593135X.
- ↑ Zimek, A.; Campello, R. J. G. B.; Sander, J. R. (2014). Ensembles for unsupervised outlier detection. ACM SIGKDD Explorations Newsletter. 15: 11—22. doi:10.1145/2594473.2594476.
- ↑ Kriegel, H.-P.; Kröger, P.; Schubert, E.; Zimek, A. (2009). LoOP: Local Outlier Probabilities (PDF). Proceedings of the 18th ACM Conference on Information and Knowledge Management. CIKM '09. с. 1649—1652. doi:10.1145/1645953.1646195. ISBN 978-1-60558-512-3.
- ↑ Kriegel, H. P.; Kröger, P.; Schubert, E.; Zimek, A. (2011). Interpreting and Unifying Outlier Scores. Proceedings of the 2011 SIAM International Conference on Data Mining. с. 13—24. CiteSeerX 10.1.1.232.2719. doi:10.1137/1.9781611972818.2. ISBN 978-0-89871-992-5.
- ↑ Schubert, E.; Wojdanowski, R.; Zimek, A.; Kriegel, H. P. (2012). On Evaluation of Outlier Rankings and Outlier Scores. Proceedings of the 2012 SIAM International Conference on Data Mining. с. 1047—1058. CiteSeerX 10.1.1.300.7205. doi:10.1137/1.9781611972825.90. ISBN 978-1-61197-232-0.


