Коядро (теорія категорій)

В теорії категорій коядро — поняття, двоїсте до ядра. Ядро є підоб'єктом прообразу, а коядро — фактороб'єктом образу.

Означення

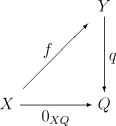
Нехай C — категорія з нульовими морфізмами. Тоді коядро морфізма f : X → Y — морфізм q : Y → Q, такий що:

• qof — нульовий морфізм із X у Q;

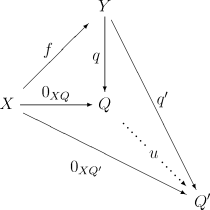
• Для будь-якого морфізма ${\displaystyle q':Y\to Q'}$, такого що ${\displaystyle q'\circ f}$ — нульовий морфізм, існує єдиний морфізм ${\displaystyle u:Q\to Q'}$, такий що наступна діаграма є комутативною:

Як і інші універсальні конструкції, коядро існує не завжди, але якщо існує, то воно є визначеним з точністю до ізоморфізму.

Коядро завжди є епіморфізмом. Навпаки, епіморфізм називається нормальним (іноді — конормальним), якщо він є коядром деякого морфізма. Категорія називається конормальною, якщо будь-який епіморфізм в ній є нормальним.

Приклади

В категорії груп, коядро гомоморфізму груп f : G → H є факторгрупою H по нормальному замиканню образу f. У випадку абелевих груп, оскільки кожна підгрупа є нормальною, coker(f) = H/im(f).

В абелевій категорії образ і кообраз морфізма задаються як

${\displaystyle \mathrm {im} (f)=\ker(\mathrm {coker} f)}$

${\displaystyle \mathrm {coim} (f)=\mathrm {coker} (\ker f)}$.

Зокрема, будь-який епіморфізм є своїм власним коядром.

Література

• И. Букур, А. Деляну Введение в теорию категорий и функторов. — М.: Мир, 1972.
• Saunders Mac Lane: Categories for the Working Mathematician, Second Edition, 1998, p. 64