梅尔刻度
此條目包含過多行話或專業術語,可能需要簡化或提出進一步解釋。 (2013年4月26日) |
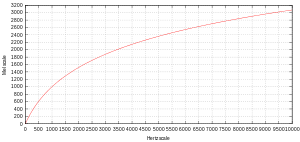

梅尔刻度(又稱Mel尺度,英語:Mel scale)是一種基于頻率定义的非線性刻度单位,表示人耳对音高(pitch)等距變化的感官,由Stevens、Volkman 和Newman于1937年命名。[1]
梅爾刻度與線性的頻率刻度赫茲(Hz)之間可以進行近似的數學換算。一个常用的将赫兹转换为梅尔的公式是:[2]
梅尔刻度將1000Hz,且高于人耳听阈值40分贝的聲音信號,定為1000mel的参考点。在頻率500Hz以上时,随着频率的增加,人耳每感覺到等量的音高變化,所需要的頻率變化愈來愈大。这导致在赫茲刻度500Hz往上的四个八度(一個八度即為兩倍的頻率),只对应梅尔刻度上的两个八度。Mel的名字来源于单词melody,表示这个刻度是基於音高比较而被創造的。
历史和其他公式
[编辑]历史上,存在过各种各样的转换公式。[3] 在O'Shaugnessy的书中的常用公式选用不同的对数底可以有不同的表达式:
对应的逆变换公式是:
自从Steinberg于1937年出版的基于最小可覺差音高的刻度曲线和表格[4] 后,还有许多其他曲线通过不同的实验方法和分析途径被提出,如Fletcher和Munson在1937年[5] ,Fletcher在1938年[6] ,Steven于1937年[1] 以及 Stevens 和 Volkmann于1940年[7] 分别给出的曲线。
在1949年,Koenig发表了一个基于独立的线性部分和对数部分的近似值,取1000Hz作为两个部分的分界点。[8]
Gunnar Fant于1949年发表了当前流行的线性\对数公式,但是有1000Hz的截止频率(corner frequency)。[9] Fant于1968年发表了该公式的另一种与对数的底数的选择无关的形式:[10][11]
1976年,Makhoul与Cosell发表了现在流行的版本,截止频率取为700Hz。[12] Ganchev等人指出:"相比于Fant等人的1000Hz的公式,700Hz的公式能够在1000Hz以下更近似于Mel刻度,代价是超过1000Hz时误差更大。"[13] 但是当频率超过7kHz时,700Hz的版本表现的更好。
这些公式的数据由Beranek于1949年基于Stevens 和 Volkman的曲线被制作成表格:[14]
| Hz | 20 | 160 | 394 | 670 | 1000 | 1420 | 1900 | 2450 | 3120 | 4000 | 5100 | 6600 | 9000 | 14000 |
| mel | 0 | 250 | 500 | 750 | 1000 | 1250 | 1500 | 1750 | 2000 | 2250 | 2500 | 2750 | 3000 | 3250 |
具有625Hz截断频率的公式由Lindsay和Norman于1977年在《Human information processing: An introduction to psychology》中提出,[15] 但在该书1972年第一版中该公式没有出现:
大多数的公式能够保证1000 mel对应1000Hz。截断频率(break frequency),如700Hz、1000Hz或625Hz,是这些公式中唯一的自由参数。一些非MEL听觉频率尺度(auditory-frequency-scale)公式使用了相同的形式,但截断频率低得多,不一定能保障1000mel对应1000Hz,例如1990年Glasberg与Moore提出的ERB-rate刻度使用的是228.8Hz[16] ,1990年Greenwood的“cochlear frequency–place map”则使用165.3Hz作为截断频率。[17]
Umesh等人对其他形式的梅尔刻度进行了研究。根据从这些曲线上计算的数据,他们指出,传统的含有对数区域和线性区域的公式,以及其他形式的公式,都不符合Stevens和Volkman的曲线:[18]
| Hz | 40 | 161 | 200 | 404 | 693 | 867 | 1000 | 2022 | 3000 | 3393 | 4109 | 5526 | 6500 | 7743 | 12000 |
| mel | 43 | 257 | 300 | 514 | 771 | 928 | 1000 | 1542 | 2000 | 2142 | 2314 | 2600 | 2771 | 2914 | 3228 |
参考文献
[编辑]- ^ 1.0 1.1 Stevens, Stanley Smith; Volkman; John; & Newman, Edwin B. A scale for the measurement of the psychological magnitude pitch. Journal of the Acoustical Society of America. 1937, 8 (3): 185–190. (原始内容存档于2013-04-14).
- ^ Douglas O'Shaughnessy. Speech communication: human and machine. Addison-Wesley. 1987: 150 [2013-04-26]. ISBN 978-0-201-16520-3. (原始内容存档于2015-03-19).
- ^
W. Dixon Ward. Musical Perception. Jerry V. Tobias (编). Foundations of Modern Auditory Theory 1. Academic Press. 1970: 412.
no one claims yet to have determined 'the' mel scale.
- ^ John C. Steinberg. Positions of stimulation in the cochlea by pure tones. Journal of the Acoustical Society of America. 1937, 8 (3): 176–180.
- ^ Harvey Fletcher and W. A. Munson. Relation Between Loudness and Masking. Journal of the Acoustical Society of America. 1937, 9: 1–10.
- ^ Harvey Fletcher. Loudness, Masking and Their Relation to the Hearing Process and the Problem of Noise Measurement. Journal of the Acoustical Society of America. 1938, 9 (4): 275–293.
- ^ Stevens, S., and Volkmann, J. The Relation of Pitch to Frequency: A Revised Scale. American Journal of Psychology. 1940, 53 (3): 329–353.
- ^ W. Koenig. A new frequency scale for acoustic measurements. Bell Telephone Laboratory Record. 1949, 27: 299–301.
- ^ Gunnar Fant (1949) "Analys av de svenska konsonantljuden : talets allmänna svängningsstruktur", LM Ericsson protokoll H/P 1064
- ^ Fant, Gunnar. (1968). Analysis and synthesis of speech processes. In B. Malmberg (Ed.), Manual of phonetics (pp. 173-177). Amsterdam: North-Holland.
- ^ Jonathan Harrington and Steve Cassidy. Techniques in speech acoustics. Springer. 1999: 18 [2013-04-26]. ISBN 978-0-7923-5731-5. (原始内容存档于2015-03-19).
- ^ John Makhoul and Lynn Cosell, LPCW: An LPC vocoder with linear predictive spectral warping, ICASSP 1976 1 (IEEE), 1976, 1: 466–469 [2013-04-26], (原始内容存档于2013-07-31)
- ^ T. Ganchev, N. Fakotakis, and G. Kokkinakis, Comparative evaluation of various MFCC implementations on the speaker verification task,, Proceedings of the SPECOM-2005, 2005: 191–194 [2013-04-26], (原始内容存档于2012-10-15)
- ^ Beranek, Leo L. (1949). Acoustic measurements. New York: McGraw-Hill.
- ^ Lindsay, Peter H.; & Norman, Donald A. (1977). Human information processing: An introduction to psychology (2nd ed.). New York: Academic Press.
- ^ B.C.J. Moore and B.R. Glasberg, "Suggested formulae for calculating auditory-filter bandwidths and excitation patterns" Journal of the Acoustical Society of America 74: 750-753, 1983.
- ^ Greenwood, D. D. (1990). A cochlear frequency–position function for several species—29 years later. The Journal of the Acoustical Society of America, 87, 2592–2605.
- ^ Umesh, S. and Cohen, L. and Nelson, D., Fitting the mel scale, Proc. ICASSP 1999 (IEEE), 1999: 217–220, ISBN 0-7803-5041-3
外部链接
[编辑]- Hz–mel, mel–Hz conversion (页面存档备份,存于互联网档案馆) (uses the O'Shaughnessy equation)
- J. Acoust. Soc. Am. table of contents for Stevens et al. paper
- Handbook for Acoustic Ecology (页面存档备份,存于互联网档案馆)







