雙代數

在數學中，域 ${\displaystyle K}$ 上的雙代數是兼具 ${\displaystyle K}$ 上之結合代數（具單位元）與餘代數的結構，而且這兩種結構彼此相容。最重要的特例之一是霍普夫代數。

定義

相容性意味著餘乘法與餘單位元都是單位結合代數的同態，這也等價於乘法及單位元是餘代數之同態，因為兩者由相同的交換圖刻画。

由單位圖表的對稱性，也可導出下述事實：如果 ${\displaystyle B}$ 是雙代數，而且 ${\displaystyle B}$ 具有良好的對偶空間 ${\displaystyle B^{\vee }}$（例如當 ${\displaystyle B}$ 維度有限時），則 ${\displaystyle B^{\vee }}$ 也帶有自然的雙代數結構。

圖表

定義中的相容性由以下交換圖給出：

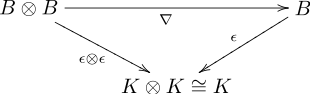
乘法與餘乘法相容：

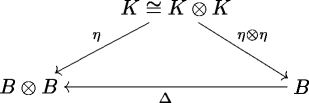
乘法與餘單位元相容：

餘乘法與單位元相容：

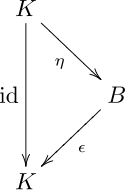
單位元與餘單位元相容：

在此 ${\displaystyle \nabla _{B}:B\otimes _{K}B\to B}$ 是代數乘法，而 ${\displaystyle \eta _{B}:K\to B}$ 是代數之單位元。${\displaystyle \Delta _{B}:B\to B\otimes _{K}B}$ 是餘代數乘法，而 ${\displaystyle \epsilon _{B}:B\to K}$ 是餘代數單位元。${\displaystyle \tau _{B}:B\otimes B\to B\otimes B}$ 定義為 ${\displaystyle \tau (x\otimes y)=y\otimes x}$。

式子

若以算式具體描述，則相容關係有如下之表示（在此採用省略 ${\displaystyle \Sigma }$ 之 Sweedler 記法）：

乘法與餘乘法相容：

${\displaystyle (ab)_{(1)}\otimes (ab)_{(2)}=a_{(1)}b_{(1)}\otimes a_{(2)}b_{(2)}\,}$

乘法與餘單位元相容：

${\displaystyle \varepsilon (ab)=\varepsilon (a)\varepsilon (b)\;}$

餘乘法與單位元相容：

${\displaystyle 1_{(1)}\otimes 1_{(2)}=1\otimes 1\,}$

單位元與餘單位元相容：

${\displaystyle \varepsilon (1)=1.\;}$

在此我們省略代數乘法之映射 ${\displaystyle \nabla }$，而直接以兩項並置表之。同理，單位元 ${\displaystyle \eta }$ 直接以單位元素 ${\displaystyle 1}$ 表示（對應到 ${\displaystyle \eta (1)}$）。

相關文獻

• Eiichi Abe, Hopf Algebras (1980), translated by Hisae Kinoshita and Hiroko Tanaka, Cambridge University Press. ISBN 0-521-22240-0

參見

• 霍普夫代數
• 餘代數
• 結合代數