Bộ tứ Anscombe

Cả bốn tập đều giống hệt nhau khi xem xét sử dụng số liệu thống kê đơn giản, nhưng khác nhau rõ rệt khi được vẽ biểu đồ.

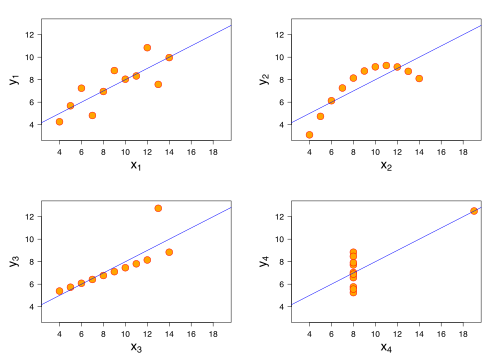
Bộ tứ Anscombe bao gồm bốn tập dữ liệu, mỗi bộ gồm mười một cặp (x, y), có những mô tả thống kê cơ bản gần như giống hệt nhau, nhưng lại có phân bố và hình dạng rất khác nhau khi được vẽ đồ thị. Chúng được xây dựng vào năm 1973 bởi nhà thống kê Francis Anscombe để cho thấy tầm quan trọng của việc vẽ đồ thị trước khi phân tích dữ liệu cũng như tác động của giá trị ngoại lai và những yếu tố khác lên các tính chất thống kê. Ông viết bài báo để phản biện lại suy nghĩ cua một số nhà thống kê rằng "tính toán số liệu là chính xác, nhưng đồ thị thì không".^[1]

Dữ liệu

Với cả bốn tập dữ liệu:

Tính chất	Giá trị	Độ chính xác
Trung bình của x	9	tuyệt đối
Phương sai mẫu của x	11	tuyệt đối
Trung bình của y	7.50	2 chữ số thập phân
Phương sai mẫu của y	4.125	±0.003
Hệ số tương quan giữa x và y	0.816	3 chữ số thập phân
Đường thẳng hồi quy tuyến tính	y = 3.00 + 0.500x	lần lượt là 2 và 3 chữ số thập phân
Hệ số xác định của hồi quy tuyến tính	0.67	2 chữ số thập phân

• Biểu đồ phân tán đầu tiên (góc trên bên trái) trông như một quan hệ tuyến tính đơn giản, tương ứng với hai ẩn tương quan và tuân theo phân phối chuẩn.
• Biểu đồ thứ hai (góc trên bên phải) không phân bố bình thường; tuy mối quan hệ giữa hai ẩn khá rõ ràng, nó không tuyến tính, và hệ số tương quan Pearson không giúp ích được gì ở đây. Một mô hình hồi quy rộng hơn và hệ số xác định tương ứng sẽ phù hợp hơn.
• Trong biểu đồ thứ ba (góc dưới bên trái), sự phân bố tuy tuyến tính nhưng nên có một đường thẳng hồi quy khác. Mô hình hồi quy có được bị lệch do một giá trị ngoại lai làm giảm hệ số tương quan từ 1 xuống 0.816.
• Cuối cùng, đồ thị thứ tư (góc dưới bên phải) cho thấy một ví dụ khi một điểm đòn bẩy đủ để cho ra một hệ số tương quan cao, ngay cả khi những điểm dữ liệu khác không cho thấy mối liên hệ nào giữa hai ẩn.

Bộ bốn này vẫn thường được dùng để cho thấy tầm quan trọng của việc nhìn vào dữ liệu bằng minh họa trước khi bắt đầu phân tích mối liên hệ, cũng như chỉ ra sự thiếu sót của những số liệu thống kê cơ bản dùng để mô ta một tập dữ liệu.^{[2][3][4][5][6]}

Bộ dữ liệu đầy đủ như sau. Giá trị x của ba tập dữ liệu đầu là giống nhau.^[1]

Bộ tứ Anscombe

I		II		III		IV
x	y	x	y	x	y	x	y
10.0	8.04	10.0	9.14	10.0	7.46	8.0	6.58
8.0	6.95	8.0	8.14	8.0	6.77	8.0	5.76
13.0	7.58	13.0	8.74	13.0	12.74	8.0	7.71
9.0	8.81	9.0	8.77	9.0	7.11	8.0	8.84
11.0	8.33	11.0	9.26	11.0	7.81	8.0	8.47
14.0	9.96	14.0	8.10	14.0	8.84	8.0	7.04
6.0	7.24	6.0	6.13	6.0	6.08	8.0	5.25
4.0	4.26	4.0	3.10	4.0	5.39	19.0	12.50
12.0	10.84	12.0	9.13	12.0	8.15	8.0	5.56
7.0	4.82	7.0	7.26	7.0	6.42	8.0	7.91
5.0	5.68	5.0	4.74	5.0	5.73	8.0	6.89

Người ta không biết Anscombe đã tạo ra bộ dữ liệu này bằng cách nào.^[7] Kể từ khi nó được xuất bản, một số phương pháp đã được phát triển để tạo ra những bộ dữ liệu tương tự với thống kê giống hệt và biểu đồ khác nhau.^[7][8]

Tham khảo

1. ^ Anscombe, F. J. (1973). “Graphs in Statistical Analysis”. American Statistician. 27 (1): 17–21. doi:10.1080/00031305.1973.10478966. JSTOR 2682899.
2. Elert, Glenn. “Linear Regression”. The Physics Hypertextbook.
3. Janert, Philipp K. (2010). Data Analysis with Open Source Tools. O'Reilly Media. tr. 65–66. ISBN 0-596-80235-8.
4. Chatterjee, Samprit; Hadi, Ali S. (2006). Regression Analysis by Example. John Wiley and Sons. tr. 91. ISBN 0-471-74696-7.
5. Saville, David J.; Wood, Graham R. (1991). Statistical Methods: The geometric approach. Springer. tr. 418. ISBN 0-387-97517-9.
6. Tufte, Edward R. (2001). The Visual Display of Quantitative Information (ấn bản thứ 2). Cheshire, CT: Graphics Press. ISBN 0-9613921-4-2.
7. ^ Chatterjee, Sangit; Firat, Aykut (2007). “Generating Data with Identical Statistics but Dissimilar Graphics: A follow up to the Anscombe dataset”. The American Statistician. 61 (3): 248–254. doi:10.1198/000313007X220057. JSTOR 27643902.
8. Matejka, Justin; Fitzmaurice, George (2017). “Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing”. Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems: 1290–1294. doi:10.1145/3025453.3025912.

Liên kết ngoài

• Khoa Vật lý, Đại học Toronto
• Anscombe's Quartet sử dụng GeoGebra cho thấy số liệu và thống kê và cho phép thay đổi những điểm dữ liệu.
• Ví dụ trực quan từ Autodesk Lưu trữ 2019-07-25 tại Wayback Machine
• Tài liệu cho bộ dữ liệu trong R.