Giản đồ Minkowski

Giản đồ Minkowski, còn được gọi là giản đồ/biểu đồ/sơ đồ Minkowski/không thời gian, được phát triển vào năm 1908 bởi Hermann Minkowski và minh họa các tính chất của không gian và thời gian trong thuyết tương đối hẹp. Nó mô tả định tính các hiện tượng như giãn nở thời gian và co ngắn chiều dài mà không cần các phương trình toán học.

Giản đồ Minkowski là các đồ thị hai chiều mô tả các sự kiện xảy ra trong vũ trụ bao gồm một chiều không gian và một chiều thời gian. Không giống như các đồ thị thời gian - khoảng cách thông thường, khoảng cách được hiển thị trên trục hoành và thời gian trên trục tung. Ngoài ra, các đơn vị đo thời gian và không gian được chọn theo cách mà một vật thể chuyển động với tốc độ ánh sáng được mô tả bởi một đường thẳng xiên góc 45 ° so với các trục của đồ thị.

Theo cách này, mỗi đối tượng, như một người quan sát hoặc một phương tiện di chuyển, đi theo một đường nhất định trên đồ thị, được gọi là tuyến thế giới của đối tượng. Ngoài ra, mỗi điểm trong đồ thị đại diện cho một vị trí nhất định trong không gian và thời gian, và được gọi là một sự kiện, bất kể có sự kiện gì xảy ra tại vị trí đó, vào thời điểm đó hay không.

Khái niệm cơ bản

Đồ thị thời gian vị trí

Trong nghiên cứu về động học 1 chiều, đồ thị thời gian - vị trí là một cách để mô tả chuyển động.

Trong hình bên, đối tượng được vẽ di chuyển ra xa khỏi gốc trục tung với tốc độ không đổi là 1,66 m/s trong sáu giây, dừng lại trong năm giây, sau đó quay trở lại điểm gốc trong khoảng thời gian bảy giây với tốc độ biến thiên.

Giản đồ không thời gian

Ở mức cơ bản nhất, giản đồ không thời gian chỉ là một đồ thị thời gian - vị trí, với hai trục tọa độ đổi chỗ cho nhau. Khi được sử dụng trong thuyết tương đối đặc hẹp, trục thời gian của giản đồ không thời gian được chia tỷ lệ với tốc độ ánh sáng $c$ , và do đó thường được dán nhãn $ct.$ Điều này thay đổi thứ nguyên của đại lượng vật lý từ < Thời gian > thành < Độ dài >, theo thứ nguyên tương ứng của trục không gian, thường được dán nhãn $x.$

Cấu hình chuẩn

Hai hệ quy chiếu Ga-li-lê S và S' (phát âm là "S phẩy"), mỗi hệ ứng với người quan sát O và O' đứng yên trong hệ quy chiếu tương ứng, nhưng chuyển đông với vận tốc ±v so với hệ quy chiếu còn lại, được gọi là ở trong cấu hình tiêu chuẩn, nếu:

Các trục x, y, z của hệ quy chiếu S được định hướng song song với các trục phẩy tương ứng của hệ quy chiếu S.
Hệ quy chiếu S′ di chuyển theo hướng x của hệ quy chiếu S với vận tốc v không đổi được đo trong hệ quy chiếu S.
Gốc của hai hệ quy chiếu S và S' trùng với thời gian t = 0 trong hệ quy chiếu S và t ′ = 0 trong hệ quy chiếu S'.^[1] ^:107

Giản đồ Minkowski

Giản đồ không thời gian trong vật lý Newton

Các trục màu đen có nhãn $x$ và $ct$ trên đồ thị kế bên là hệ tọa độ của người quan sát, được gọi là 'hệ tọa độ nghỉ' và người quan sát được định vị ở x = 0. Tuyến thế giới của người quan sát này đồng nhất với trục thời gian $ct$ . Mỗi đường thẳng song song với trục này cũng tương ứng với một đối tượng ở trạng thái nghỉ nhưng ở một vị trí khác. Đường màu xanh mô tả một vật thể chuyển động với tốc độ $v$ không đổi sang phải, chẳng hạn như một người quan sát chuyển động.

Đường màu xanh có nhãn $ct'$ có thể được hiểu là trục thời gian cho người quan sát thứ hai. Trục ct' cùng với trục $x$ , giống hệt nhau cho cả hai người quan sát, tạo thành hệ tọa độ cho người quan sát thứ hai.

Thời gian của sự kiện A trong giản đồ là như nhau cho cả hai người quan sát. Chỉ có vị trí là có giá trị khác nhau.

Giản đồ Minkowski trong thuyết tương đối hẹp

Năm 1905, Albert Einstein đã phát hiện ra thuyết tương đối hẹp,^[2] và năm 1908 Hermann Minkowski cung cấp một giản đồ minh họa.^[3]

Trong giản đồ Minkowski, tính tương đối của sự đồng thời tương ứng với việc đặt một trục $x'$ riêng cho người quan sát di chuyển. Theo quy tắc được mô tả ở trên, mỗi người quan sát diễn giải tất cả các sự kiện trên một đường thẳng song song với trục $x$ (hoặc là $x'$ ) là đồng thời. Chuỗi các sự kiện từ góc nhìn của người quan sát có thể được minh họa bằng cách dịch chuyển song song đường thẳng này trong giản đồ từ dưới lên trên.

Nếu $ct$ thay vì $t$ được gán trên trục thời gian, góc $α$ giữa các trục $x$ và $x'$ sẽ bằng góc giữa các trục thời gian $ct$ và $ct'$ . Điều này xuất phát từ tiên đề thứ hai của thuyết tương đối hẹp, nói rằng tốc độ ánh sáng là như nhau đối với tất cả mọi người quan sát, bất kể chuyển động tương đối của họ. Góc $α$ được cho bởi ^[4]

\tan(\alpha )={\frac {v}{c}}=\beta

.

Độ chia trên các trục được cho như sau: Nếu $U$ là độ dài đơn vị trên trục của $ct$ và $x$ tương ứng, thì độ dài đơn vị trên trục $ct'$ và $x'$ là:^[5]

U'=U\cdot {\sqrt {\frac {1+\beta ^{2}}{1-\beta ^{2}}}}\,.

Trục $ct$ đại diện cho tuyến thế giới của một chiếc đồng hồ đứng yên $S$ , với $U$ đại diện cho thời gian giữa hai sự kiện xảy ra trên tuyến này, còn được gọi là thời gian riêng giữa các sự kiện này. Độ dài $U$ trên trục $x$ biểu thị độ dài nghỉ hoặc độ dài riêng của một thanh đứng yên trong $S$ Tương tự với khoảng cách $U'$ trên $ct'$ và $x'$ của $S'$ .

Giản đồ Loedel

Giãn nở thời gian

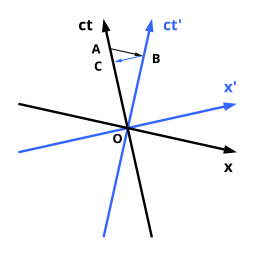
Co ngắn chiều dài

Sự không đổi của tốc độ ánh sáng

Tốc độ ánh sáng và quan hệ nhân quả

Giản đồ không thời gian của một người quan sát tăng tốc trong thuyết tương đối hẹp

Các hệ quy chiếu quán tính cùng chuyển động (nhất thời) với một người quan sát đang tăng tốc nhanh.

Trục tung biểu thị thời gian, trục hoành biểu thị khoảng cách, đường đứt nét là tuyến thế giới của người quan sát. Các chấm nhỏ là các sự kiện cụ thể trong không thời gian. Nếu ta tưởng tượng những sự kiện này là một ánh sáng nhấp nháy, thì những sự kiện vượt qua hai đường chéo ở nửa dưới của hình ảnh (nón ánh sáng quá khứ của người quan sát ở gốc) là những sự kiện mà người quan sát thấy được. Độ dốc của tuyến thế giới (độ lệch so với phương thẳng đứng) cho ta vận tốc tương đối của người quan sát. Lưu ý cách hệ quy chiếu quán tính nhất thời thay đổi khi người quan sát tăng tốc.

Xem thêm

Giản đồ Penrose
Không gian Minkowski

Tham khảo

^ Collier, Peter (2017). A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity (ấn bản thứ 3). Incomprehensible Books. ISBN 9780957389465.
^ Einstein, Albert (1905). “Zur Elektrodynamik bewegter Körper” [On the electrodynamics of moving bodies] (PDF). Annalen der Physik. 322 (10): 891–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004.. See also: English translation.
^ Minkowski, Hermann (1909). “Raum und Zeit” [Space and time]. Physikalische Zeitschrift. 10: 75–88.
^ Demtröder, Wolfgang (2016). Mechanics and Thermodynamics . Springer. tr. 92–93. ISBN 978-3-319-27877-3. Extract of page 93
^ Freund, Jürgen (2008). Special Relativity for Beginners: A Textbook for Undergraduates. World Scientific. tr. 49. ISBN 978-9812771599.

Anthony French (1968) Special Relativity, pages 82 & 83, New York: W W Norton & Company.
E.N. Glass (1975) "Lorentz boosts and Minkowski diagrams" American Journal of Physics 43:1013,4.
N. David Mermin (1968) Space and Time in Special Relativity, Chapter 17 Minkowski diagrams: The Geometry of Spacetime, pages 155–99 McGraw-Hill.
Rindler, Wolfgang (2001). Relativity: Special, General and Cosmological. Oxford University Press. ISBN 0-19-850836-0.
W.G.V. Rosser (1964) An Introduction to the Theory of Relativity, page 256, Figure 6.4, London: Butterworths.
Edwin F. Taylor and John Archibald Wheeler (1963) Spacetime Physics, pages 27 to 38, New York: W. H. Freeman and Company, Second edition (1992).
The Symbolic Universe: Geometry and Physics, 1999 (see page 10 of e-link)

Liên kết ngoài

[Collier-1] Collier, Peter (2017). A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity (ấn bản thứ 3). Incomprehensible Books. ISBN 9780957389465.

[2] Einstein, Albert (1905). “Zur Elektrodynamik bewegter Körper” [On the electrodynamics of moving bodies] (PDF). Annalen der Physik. 322 (10): 891–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004.. See also: English translation.

[minko-3] Minkowski, Hermann (1909). “Raum und Zeit” [Space and time]. Physikalische Zeitschrift. 10: 75–88.

[4] Demtröder, Wolfgang (2016). Mechanics and Thermodynamics . Springer. tr. 92–93. ISBN 978-3-319-27877-3. Extract of page 93

[5] Freund, Jürgen (2008). Special Relativity for Beginners: A Textbook for Undergraduates. World Scientific. tr. 49. ISBN 978-9812771599.

[1]

[2]

[3]

[4]

[5]