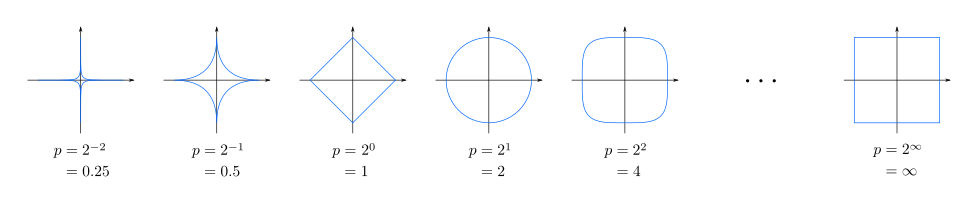Hình cầu đơn vị

Một số lĩnh vực. ${\displaystyle \|{\boldsymbol {x}}\|_{2}}$ là chuẩn cho không gian Euclide, thảo luận trong phần đầu tiên bên dưới.

Trong toán học, một đơn vị cầu là các tập hợp của các điểm có khoảng cách 1 từ một điểm trung tâm cố định, nơi mà một khái niệm tổng quát về khoảng cách có thể định nghĩa một trái bóng đơn vị kín, là các tập hợp của các điểm có khoảng cách ít hơn hoặc bằng 1 từ một cố định điểm trung tâm. Thường là một cụ thể điểm đã được phân biệt như là gốc tọa độ của không gian đang được xét và nó được hiểu là một cầu đơn vị hoặc đơn vị bóng được tập trung tại thời điểm đó. Vì vậy, người ta nói về "đơn vị" bóng hoặc "đơn vị" hình cầu..

Ví dụ, hình cầu một chiều là bề mặt của những gì thường được gọi là "vòng tròn", trong đó một bên trong vòng tròn và bề mặt của nó là hai chiều quả bóng. Tương tự, một hình cầu hai chiều là bề mặt của thể Euclid thường được biết đến như một "hình cầu", trong khi bên trong và bề mặt cùng là ba chiều bóng.

Một đơn vị cầu chỉ là một cầu có bán kính 1. Tầm quan trọng của các đơn vị cầu đó là lĩnh vực bất kỳ, có thể chuyển đến một đơn vị cầu bởi một sự kết hợp của bản dịch và rộng. Bằng cách này các đặc tính của lĩnh vực chung có thể giảm cho việc nghiên cứu của các cầu đơn vị.

Hình cầu đơn vị và quả bóng trong không gian Euclid

Trong không gian Euclid của n kích thước, các cầu đơn vị là các tập hợp của tất cả các điểm ${\displaystyle (x_{1},\ldots ,x_{n})}$ đáp ứng các phương trình

${\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}=1.}$

Một quả bóng đơn vị mở là các tập hợp của tất cả các điểm thỏa mãn sự bất đẳng thức

${\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}<1,}$

và quả bóng đơn vị đóng là các thiết lập của tất cả các điểm thỏa mãn sự bất đẳng thức

${\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}\leq 1.}$

Tổng diện tích và công thức thể tích

Phương trình cổ điển của một cầu đơn vị là các nguồn với một bán kính 1 và không thay đổi trong x-, y- hay z- trục:

${\displaystyle f(x,y,z)=x^{2}+y^{2}+z^{2}=1}$

Thể tích của quả bóng đơn vị trong không gian Euclid n-chiều, và diện tích bề mặt của cầu đơn vị, xuất hiện trong nhiều công thức quan trọng của phân tích. Thể tích của quả bóng đơn vị trong n chiều, mà được ký hiệu V_n, có thể mô tả bằng cách sử dụng phương trình gamma. Nó là

${\displaystyle V_{n}={\frac {\pi ^{n/2}}{\Gamma (1+n/2)}}={\begin{cases}{\pi ^{n/2}}/{(n/2)!}&\mathrm {if~} n\geq 0\mathrm {~is~even,} \\~\\{\pi ^{\lfloor n/2\rfloor }2^{\lceil n/2\rceil }}/{n!!}&\mathrm {if~} n\geq 0\mathrm {~is~odd,} \end{cases}}}$

ở đây n!! là đôi thừa (hay giai thừa kép).

Các hypervolume của (n−1)-chiều cầu đơn vị (tức là, "diện tích" của bề mặt của n-chiều đơn vị bóng), mà chúng ta biểu thị A_n, có thể biểu diễn như

${\displaystyle A_{n}=nV_{n}={\frac {n\pi ^{n/2}}{\Gamma (1+n/2)}}={\frac {2\pi ^{n/2}}{\Gamma (n/2)}}\,,}$

ở đây đẳng thức cuối giữ chỉ cho n > 0.

Diện tích bề mặt và thể tích cho một số giá trị của ${\displaystyle }$ như sau:

${\displaystyle n}$	${\displaystyle A_{n}}$ (surface area)		${\displaystyle V_{n}}$ (volume)
0	${\displaystyle 0(1/0!)\pi ^{0}}$	0	${\displaystyle (1/0!)\pi ^{0}}$	1
1	${\displaystyle 1(2^{1}/1!!)\pi ^{0}}$	2	${\displaystyle (2^{1}/1!!)\pi ^{0}}$	2
2	${\displaystyle 2(1/1!)\pi ^{1}=2\pi }$	6.283	${\displaystyle (1/1!)\pi ^{1}=\pi }$	3.141
3	${\displaystyle 3(2^{2}/3!!)\pi ^{1}=4\pi }$	12.57	${\displaystyle (2^{2}/3!!)\pi ^{1}=(4/3)\pi }$	4.189
4	${\displaystyle 4(1/2!)\pi ^{2}=2\pi ^{2}}$	19.74	${\displaystyle (1/2!)\pi ^{2}=(1/2)\pi ^{2}}$	4.935
5	${\displaystyle 5(2^{3}/5!!)\pi ^{2}=(8/3)\pi ^{2}}$	26.32	${\displaystyle (2^{3}/5!!)\pi ^{2}=(8/15)\pi ^{2}}$	5.264
6	${\displaystyle 6(1/3!)\pi ^{3}=\pi ^{3}}$	31.01	${\displaystyle (1/3!)\pi ^{3}=(1/6)\pi ^{3}}$	5.168
7	${\displaystyle 7(2^{4}/7!!)\pi ^{3}=(16/15)\pi ^{3}}$	33.07	${\displaystyle (2^{4}/7!!)\pi ^{3}=(16/105)\pi ^{3}}$	4.725
8	${\displaystyle 8(1/4!)\pi ^{4}=(1/3)\pi ^{4}}$	32.47	${\displaystyle (1/4!)\pi ^{4}=(1/24)\pi ^{4}}$	4.059
9	${\displaystyle 9(2^{5}/9!!)\pi ^{4}=(32/105)\pi ^{4}}$	29.69	${\displaystyle (2^{5}/9!!)\pi ^{4}=(32/945)\pi ^{4}}$	3.299
10	${\displaystyle 10(1/5!)\pi ^{5}=(1/12)\pi ^{5}}$	25.50	${\displaystyle (1/5!)\pi ^{5}=(1/120)\pi ^{5}}$	2.550

ở đây, các giá trị mở rộng thập phân cho n ≥ 2 được làm tròn đến giá trị gần đúng.

Đệ quy

Các giá trị A_n thỏa mãn đệ quy:

${\displaystyle A_{0}=0}$

${\displaystyle A_{1}=2}$

${\displaystyle A_{2}=2\pi }$

${\displaystyle A_{n}={\frac {2\pi }{n-2}}A_{n-2}}$ cho ${\displaystyle n>2}$.

Các giá trị V_n thỏa mãn đệ quy:

${\displaystyle V_{0}=1}$

${\displaystyle V_{1}=2}$

${\displaystyle V_{n}={\frac {2\pi }{n}}V_{n-2}}$ cho ${\displaystyle n>1}$.

Thứ nguyên phân số

Các công thức cho A_n và V_n có thể được tính cho số thực bất kỳ n ≥ 0, và có những trường hợp theo đó nó là thích hợp để tìm kiếm diện tích hình cầu hoặc khối lượng bóng khi n không phải là một số nguyên không âm.

Biểu đồ này cho thấy siêu thể tích của một hình cầu (x–1)-chiều (tức là, "diện tích" của bề mặt của x-chiều đơn vị bóng) như là một hàm liên tục của x.

Biểu đồ này cho thấy thể tích của một bóng trong x-chiều như một hàm liên tục của x.

Khác bán kính

Diện tích bề mặt của một quả cầu (n-1) chiều có bán kính r là A_n rⁿ⁻¹ và thể tích của quả bóng đơn vị n-chiều với bán kính r là V_n rⁿ. Ví dụ, diện tích là A = 4π r² với bề mặt của quả bóng ba chiều bán kính r. Thể tích là V = 4π r³ / 3 với quả bóng ba chiều bán kính r.

Quả cầu đơn vị trong véc tơ không gian chuẩn hóa

Chính xác hơn, quả bóng đơn vị mở trong một không gian véc-tơ chuẩn hóa ${\displaystyle V}$, với chuẩn ${\displaystyle \|\cdot \|}$, là

${\displaystyle \{x\in V:\|x\|<1\}.}$

Đó là phần trong của quả bóng đơn vị đóng của (V,||·||),

${\displaystyle \{x\in V:\|x\|\leq 1\}.}$

Sau đó là sự kết hợp phần tách rời và đường biên chung của chúng, các đơn vị cầu của (V,||·||),

${\displaystyle \{x\in V:\|x\|=1\}.}$

Các hình ảnh của các bóng đơn vị là hoàn toàn phụ thuộc vào các lựa chọn chuẩn hóa, nó cũng có thể có 'góc' và ví dụ có thể trông giống như [−1,1]ⁿ, trong trường hợp của chuẩn l_∞ ở Rⁿ. Các vòng bóng được hiểu là bình thường của chuẩn hóa không gian Hilbert, dựa trên trường hợp chiều hữu hạn của đường Euclid khoảng cách; ranh giới của nó là những gì thường được có nghĩa là bởi các đơn vị cầu. Ở đây là một số hình ảnh của các đơn vị bóng cho hai chiều ${\displaystyle \ell ^{p}}$ không gian cho giá trị khác nhau của p (bóng đơn vị bị lõm cho p < 1 và lồi cho p ≥ 1):

Những điều này minh hoạ tại sao điều kiện p ≥ 1 là cần thiết trong định nghĩa của chuẩn ${\displaystyle \ell ^{p}}$, như các đơn vị bóng trong bất kỳ định chuẩn không phải là lồi như một hệ quả của bất đẳng thức tam giác.

Lưu ý rằng trong chu vi ${\displaystyle C_{p}}$ của quả cầu đơn vị hai chiều, ta có:

${\displaystyle C_{0}=C_{\infty }=8}$ là giá trị lớn nhất.

${\displaystyle C_{1}=4{\sqrt {2}}}$ là giá trị nhỏ nhất.

${\displaystyle C_{2}=2\pi \,.}$

Tổng quát

Không gian số liệu

Tất cả ba ở trên nghĩa, có thể là dàng tổng quát một số liệu không gian, đối với một lựa chọn nguồn gốc. Tuy nhiên, tô pô cân nhắc (bên trong, đóng cửa biên giới) không cần phải áp dụng trong cùng một cách (ví dụ như, trong ultrametric không gian, tất cả các ba là cùng một lúc mở và đóng bộ), và các cầu đơn vị thậm chí có thể là trống rỗng trong một không gian số liệu.

Các hình thức dạng bậc hai

Nếu V là một tuyến không gian với một bậc mẫu F:V → R, sau đó { p ∈ V : F(p) = 1 } có thể được gọi là cầu đơn vị^[1][2] hoặc đơn vị bán cầu của V. Ví dụ, các bậc hình thức ${\displaystyle }$khi bộ bằng một, tạo ra các đơn vị hyperbol mà đóng vai trò của "vòng tròn đơn vị" trong các máy bay của chia số phức hợp. Tương tự, bậc hình x² mang một cặp đường cho các cầu đơn vị trong mặt phẳng hai số.

Xem thêm

• Quả cầu
• Mặt cầu
• Danh sách ký hiệu toán học
• Đường tròn đơn vị
• Hình vuông đơn vị

Ghi chú và tài liệu tham khảo

1. Takashi Ono (1994) Variations on a Theme of Euler: quadratic forms, elliptic curves, and Hopf maps, chapter 5: Quadratic spherical maps, page 165, Plenum Press, ISBN 0-306-44789-4
2. F. Reese Harvey (1990) Spinors and calibrations, "Generalized Spheres", page 42, Academic Press, ISBN 0-12-329650-1

• Nghiệp đó M. Ngày (Năm 1958) định chuẩn Tuyến không Gian, trang 24, Springer Nghề.
• Deza, E.; Deza, M. (2006), Dictionary of Distances, Elsevier, ISBN 0-444-52087-2. Xem bản ngắn gọn tại Jeff Pratt (24 tháng 6 năm 2007). “Bản tin của Hiệp hội Toán học châu Âu”. tr. 57.

Đường dẫn ngoài