Mẫu (thống kê)
Trong nghiên cứu thống kê và phương pháp nghiên cứu định lượng, một mẫu dữ liệu là một tập hợp các dữ liệu thu thập được và/ hoặc được lựa chọn từ một tổng thể thống kê bằng một quy tắc rõ ràng.[1]
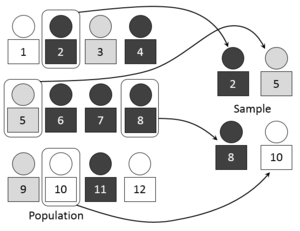
Thông thường, tổng thể rất lớn, làm cho việc tính toán tổng thể nhằm mục đích thống kê hoặc một liệt kê đầy đủ của tất cả các giá trị trong tổng thể không thực tế hoặc tổng thể có thể tồn tại. Các mẫu thường đại diện cho một tập hợp con của kích thước mẫu tổng thể. Các mẫu được thu thập và thống kê được tính toán từ các mẫu để có thể kết luận hoặc ngoại suy từ các mẫu đến tổng thể. Quá trình của thu thập thông tin từ một mẫu được gọi là lấy mẫu. Các mẫu dữ liệu có thể được rút ra từ một tổng thể mà không cần trả lại, trong trường hợp này nó là một tập hợp con của một tổng thể. Hoặc mẫu thay thế trong trường hợp nó là nhiều tập hợp con.[2]
Các kiểu mẫu
[sửa | sửa mã nguồn]Một mẫu hoàn chỉnh là một tập hợp các đối tượng từ một mẫu mẹ bao gồm tất cả các đối tượng đáp ứng một tập hợp của tiêu chuẩn lựa chọn các đặc điểm được định nghĩa rõ ràng.[3] Ví dụ một mẫu đầy đủ của “những người đàn ông nước Úc cao hơn 2m” sẽ bao gồm một danh sách của tất cả các ngươi đàn ông cao hơn 2m. Nhưng nó không bao gồm những người đàn ông Đức, hoặc những người phụ nữ Úc thấp hơn 2m. Vì vậy để tổng hợp một mẫu đầy đủ yêu cầu một danh sách đầy đủ của tổng tể mẫu mẹ, bao gồm dữ liệu về chiều cao, giới tính, quốc tịch cho mỗi thành viên trong mẫu mẹ. Trong trường hợp tổng thể con người, một danh sách đầy đủ dường như không tồn tại, nhưng các mẫu đầy đủ thường có trong các ngành khác, ví dụ như mẫu có độ lớn giới hạn của tổng thể của các đối tượng vô cùng to lớn.
Một mẫu không có thành kiến (đại diện) là một tập hợp các đối tượng được lựa chọn từ một mẫu hoàn chỉnh bằng cách sử dụng một tiến trình lựa chọn không phụ thuộc vào tính chất của các đối tượng.[4] Ví dụ một mẫu không chệch “đàn ông Úc cao hơn 2m” có thể bao gồm lấy mẫu ngẫu nhiên tập hợp mẫu con của 1% nam giới Úc cao hơn 2m. Nhưng có một quyết định từ mẫu trong đó mỗi danh sách cử tri chính thức có thể không phải là mẫu không chệch, ví dụ nam giới ở độ tuổi dưới 18 sẽ không được ứng cử. Trong một đối tượng lớn, một mẫu ngẫu nhiên có thể gồm có phân số của mẫu tổng thể cho những dữ liệu mẫu có sẵn, cung cấp các dữ liệu có sẵn không chệch bởi những thuộc tính riêng biệt.
Cách tốt nhất để tránh một mẫu chệch hay không có tính đại diện là chọn mẫu ngẫu nghiên, cũng được xem như là một xác suất. Một mẫu ngẫu nhiên được định nghĩa như là một mẫu trong đó mỗi cá thể riêng lẻ của tổng thể có thể phân biệt được, không một xác suất ngẫu nhiên của việc chọn mẫu được xem như một phần của mẫu.[5] Một số loại mẫu ngẫu nhiên không có nhiều yếu tố, mẫu có hệ thống, phân lớp mẫu ngẫu nhiên.
Một mẫu không phải là ngẫu nhiên được gọi là chọn mẫu không ngẫu nhiên hay chọn mẫu không có xác suất.[6] Một ví dụ về các mẫu không ngẫu nhiên là mẫu thuận lợi, mẫu phán đoán, mẫu có chủ đích, mẫu quota, mẫu dây chuyền, giao điểm vuông góc trong phương pháp giống như Monte Carlo.
Mẫu số liệu thống kê được sử dụng nhiều. Chúng có thể được sử dụng trong nhiều tình huống.
Mô tả toán học của mẫu ngẫu nhiên
[sửa | sửa mã nguồn]Trong các thuật ngữ toán học, đưa ra một đại lượng ngẫu nhiên X có phân phối F, một mẫu ngẫu nhiên có độ dài n (n có thể là bất kỳ của 1, 2, 3....) là một tập hợp của n độc lập, tương tự như phân phối các đại lượng ngẫu nhiên với phân phối F.[7]
Một đại diện chọn mẫu cho n thí nghiệm trong cùng số lượng mẫu được đo. Ví dụ, nếu X đại diện cho chiều cao của một cá thể và cá thể n có nghĩa, sẽ là chiều cao của i-th cá thể. Lưu ý rằng một mẫu của các biến ngẫu nhiên (tức là một tập hợp các chức năng đo lường được) không được nhầm lẫn với nghững thử nghiệm của các biến này (những giá trị được chọn thử nghiệm ngẫu nhiên, được gọi là các biến ngẫu nhiên). Nói cách khác là một hàm đại diện cho các phép đo trong thứ nghiệm thứ i và là giá trị thực thu được khi thực hiện phép đo.
Khái niệm của một mẫu bao gồm quá trình của việc làm cách nào để thu được dữ liệu (các biến ngẫu nhiên). Điều này rất cần thiết để báo cáo trong toán học có thể được thực hiện các mẫu và số liệu thống kê, như trung bình mẫu và phương sai.
Tham khảo
[sửa | sửa mã nguồn]- ^ Peck, Roxy; Chris Olsen; Jay L. Devore (2008). Introduction to Statistics and Data Analysis (ấn bản thứ 3). Cengage Learning. ISBN 0-495-55783-8. Truy cập ngày 4 tháng 8 năm 2009.
- ^ Borzyszkowski, Andrzej M.; Sokołowski, Stefan, biên tập (1993), Mathematical Foundations of Computer Science 1993. 18th International Symposium, MFCS'93 Gdańsk, Poland, August 30–ngày 3 tháng 9 năm 1993 Proceedings, Lecture Notes in Computer Science, quyển 711, tr. 281–290, doi:10.1007/3-540-57182-5_20, ISBN 978-3-540-57182-7, Zbl 0925.11026
- ^ Pratt, J. W., Raiffa, H. and Schaifer, R. (1995). Introduction to Statistical Decision Theory. MIT Press, Cambridge,MA. MR1326829
- ^ Lomax, R. G. and Hahs-Vaughan, Debbie L. An introduction to statistical concepts (3rd ed).
- ^ Cochran, William G. (1977). Sampling techniques . Wiley. ISBN 0-471-16240-X.
- ^ Johan Strydom (2005). Introduction to Marketing . Wiley. ISBN 0-471-16240-X.
- ^ Samuel S. Wilks, Mathematical Statistics, John Wiley, 1962, Section 8.1
Liên kết ngoài
[sửa | sửa mã nguồn] GIẢM
11%
GIẢM
11%
 GIẢM
50%
GIẢM
50%
 GIẢM
13%
GIẢM
13%
 GIẢM
20%
GIẢM
20%
![[Review Sách] Suy tưởng](https://down-bs-vn.img.susercontent.com/vn-11134207-7r98o-llnmys2twmz345.webp) GIẢM
3%
GIẢM
3%






