Antiprisma

Antiprisma

Tipus	figura isogonal, prismatoide i políedre uniforme
Forma de les cares	polígon (2) triangle ()
Dual	trapezoedre
Elements
Cares	2 p-gons, 2p triangles
Arestes	4p
Vèrtexs	2p
Més informació
MathWorld	Antiprism

Un antiprisma és un políedre que es caracteritza per tenir dues cares iguals paral·leles, però a diferència del prisma, estan unides per mitjà de triangles.

En el cas dels antiprismes de directrius regulars, les dues cares directrius són polígons regulars i tots els triangles circumdants són equilàters, cosa que fa que el cos siga d'arestes regulars (totes iguals). En general les cares paral·leles d'un antiprisma de directrius regulars estan girades l'una de l'altra en un angle β:

β = 360° / 2n

on n és el nombre de costats del polígon regular.

Antiprisma uniforme

Un antiprisma uniforme té, a part de les cares de les bases, 2n triangles equilàters com a cares. Com a classe, els antiprismes uniformes formen una sèrie infinita de políedres vèrtexuniformes, igual que els prismes uniformes. Per a n = 2 tenim el cas degenerat del tetràedre com a antiprisma digonal, i per a n = 3 l'octàedre regular no-degenerat com a antiprisma triangular.

Els políedres duals dels antiprismes són els trapezòedres. Johannes Kepler fou el primer en duscutir la seva existència i en atribuir-los el nom.

Família d'antiprismes uniformes n.3.3.3

V2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3

Diagrames de Schlegel

A3

A4

A5

A6

A7

A8

Coordenades cartesianes

Les coordenades cartesianes per als vèrtexs d'un antiprisma recte amb bases n-gonals i triangles isòsceles són

${\displaystyle \left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)}$

amb k variant des de 0 fins a 2n−1; si els triangles són equilàters,

${\displaystyle 2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.}$

Volum i àrea de la superfície

Sigui a la longitud de les arestes d'un antiprisma uniforme. Llavors el seu volum és

${\displaystyle V={\frac {n{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}\;a^{3}}$

i l'àrea de la superfície és

${\displaystyle A={\frac {n}{2}}(\cot {\frac {\pi }{n}}+{\sqrt {3}})a^{2}.}$

Políedres relacionats

Existeix un conjunt infinit d'antiprismes truncats, incloent-hi una forma simètrica de l'octàedre truncat.

Antiprismes
				...
s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,2n}
Antiprismes truncats
				...
ts{2,4}	ts{2,6}	ts{2,8}	ts{2,10}	ts{2,2n}
Antiprismes xatos (snub (anglès))
J84	Icosàedre	J85	Irregulars...
				...
ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}	ss{2,2n}

Simetria

El grup de simetria d'un antiprisma de n cares recte amb base regular i cares laterals isòsceles és D_nd d'ordre 4n, excepte en el cas d'un tetràedre, que té un grup de simetria més gran, T_d d'ordre 24, que té tres versions de D_2d com a subgrups, i l'octàedre, que té un grup de simetria més gran, O_h d'ordre 48, que té quatre versions de D_3d com a subgrups.

El grup de simetria conté inversions si i només si n és senar.

El grup de rotació és D_n d'ordre 2n, excepte en el cas d'un tetràedre, que té el grup de rotació T d'ordre 12, que té tres versions de D₂ com a subgrups; i l'octàedre, que té el grup de rotació O d'ordre 24, que té quatre versions de D₃ com a subgrups.

Antiprisma estrellat

5/2-antiprisma		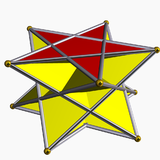	5/3-antiprisma
9/2-antiprisma		9/4-antiprisma		9/5-antiprisma

Aquesta figura mostra tots els antiprismes no-estrellats i estrellats de fins a 15 cares, juntament a aquells d'un 29-gon.

Els antiprismes estrellats uniformes s'anomenen per les seves bases en forma de polígon estrellat, {p/q}, i existeixen en les seves variants prògrades i retrògrades (creuades). Les formes creuades tenen figures de vèrtex intersecants, i es denoten amb fraccions invertides, p/(p-q) en comptes de p/q, com per exemple 5/3 en comptes de 5/2.

En les formes retrògrades, però no en les formes prògrades, els triangles que uneixen les bases estrellades intersecten l'eix de la simetria rotacional.

Alguns antiprismes estrellats retrògrads amb bases estrellades regulars no es poden construir amb arestes d'igual longitud, de tal manera que no són políedres uniformes. Els compostos d'antiprismes estrellats també es poden construir quan p i q tenen factors comuns; així, un antiprisma 10/4 és el compost de dos antiprismes estrellats 5/2.

Antiprismes estrellats uniformes per simetria, fins a 12

Grup de simetria	Formes estrellades
d5h [2,5] (*225)	3.3.3.5/2
d5d [2^+,5] (2*5)	3.3.3.5/3
d7h [2,7] (*227)	3.3.3.7/2	3.3.3.7/4
d7d [2^+,7] (2*7)	3.3.3.7/3
d8d [2^+,8] (2*8)	3.3.3.8/3	3.3.3.8/5
d9h [2,9] (*229)	3.3.3.9/2	3.3.3.9/4
d9d [2^+,9] (2*9)	3.3.3.9/5
d10d [2^+,10] (2*10)	3.3.3.10/3
d11h [2,11] (*2.2.11)	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
d11d [2^+,11] (2*11)	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
d12d [2^+,12] (2*12)	3.3.3.12/5	3.3.3.12/7
...

Bibliografia

• Anthony Pugh. Polyhedra: A visual approach. California: University of California Press Berkeley, 1976. ISBN 0-520-03056-7.  Chapter 2: Archimedean polyhedra, prisma and antiprisms

Vegeu també

• Prisma
• Arquimedes
• Plató
• Sòlids de Johnson
• Sòlids de Kepler-Poinsot
• One World Trade Center, un edifici consistent principalment d'un antiprisma quadrat allargat^[1]

Referències

1. Kabai, Sándor. «One World Trade Center Antiprism». Wolfram Demonstrations Project. [Consulta: 8 octubre 2013].