Johannes Kepler
Johannes Kepler | |
|---|---|
 Tranh chân dung của Kepler được vẽ bởi một họa sĩ vô danh, 1620 | |
| Sinh | 27 tháng 12 năm 1571 Weil der Stadt, Đế quốc La Mã Thần thánh |
| Mất | 15 tháng 11 năm 1630 (58 tuổi) Regensburg, Đế quốc La Mã Thần thánh |
| Quốc tịch | Đức |
| Trường lớp | Tübinger Stift, Đại học Tübingen (M.A., 1591)[1] |
| Nổi tiếng vì | Định luật về chuyển động của các hành tinh Giả thiết Kepler |
| Sự nghiệp khoa học | |
| Ngành | Thiên văn học, Chiêm tinh học, Toán học và Triết học tự nhiên |
| Nơi công tác | Đại học Linz |
| Ảnh hưởng bởi | Nicolaus Copernicus Tycho Brahe Pythagoras |
| Ảnh hưởng tới | Sir Isaac Newton Benoit Mandelbrot Thomas Browne |
| Chữ ký | |
Johannes Kepler (tiếng Đức: [joˈhanəs ˈkɛplɐ, -nɛs -] ⓘ;[2][3] phiên âm tiếng Việt: Giô-han Kê-ple; sinh ngày 27 tháng 12 năm 1571 – mất ngày 15 tháng 11 năm 1630) là một nhà toán học, thiên văn học và chiêm tinh học người Đức. Là một trong những đại diện của cuộc cách mạng khoa học thế kỷ 17, Kepler được biết đến nhiều nhất bởi các định luật về chuyển động thiên thể mang tên ông do các nhà thiên văn học thiết lập dựa trên những công trình của ông như Astronomia nova, Harmonice Mundi và cuốn Thiên văn học Copernicus giản lược.
Khởi đầu sự nghiệp, Kepler từng là một giáo viên Toán ở chủng viện Graz, trước khi đảm nhiệm vai trò trợ tá cho nhà Thiên văn Tycho Brahe, và cuối cùng trở thành nhà Thiên văn học triều đình cho Hoàng đế La Mã Thần thánh Rudolf II và sau đó là các hoàng đế kế vị Matthias và Ferdinand II. Trong những năm biến động cuối đời, ông dạy toán ở Linz (Áo) và là cố vấn cho Albrecht von Wallenstein. Được biết đến chủ yếu ngày nay vì những nghiên cứu thiên văn học, ông còn có những công trình quan trọng trong lĩnh vực quang học, phát minh ra một mẫu kính viễn vọng phản xạ (Kính viễn vọng Kepler), và thảo luận về những khám phá bằng kính viễn vọng của một nhà khoa học sống cùng thời, Galileo Galilei.
Kepler sống trong một thời đại mà giữa thiên văn và chiêm tinh không có sự phân biệt rõ ràng, nhưng có sự chia tách giữa thiên văn (như một nhánh của toán học) và vật lý (một nhánh của triết học tự nhiên). Kepler cũng kết hợp lý lẽ và lập luận tôn giáo vào công trình của mình, được thúc đẩy bởi đức tin rằng Chúa đã tạo ra thế giới theo một kế hoạch khả tri mà con người có thể lĩnh hội qua ánh sáng của lý trí.[4] Kepler mô tả nền Thiên văn học mới của ông là "Vật lý học thiên thể",[5] như "một cuộc dạo chơi vào siêu hình học của Aristotle",[6] và "một sự bổ sung cho tiểu luận Về bầu trời của Aristotle",[7] biến đổi truyền thống cổ đại về Vũ trụ học Vật lý với việc xem Thiên văn là một phần của một Vật lý học Toán học phổ quát.[8]
Những năm đầu đời
[sửa | sửa mã nguồn]

Kepler sinh ngày 27 tháng 12 năm 1571 tại thành phố tự trị Weil der Stadt thuộc Đế quốc La Mã Thần thánh (nay là một phần thuộc vùng Stuttgart ở bang Baden-Württemberg của nước Đức, cách trung tâm Stuttgart 30 km về phía tây). Ông nội ông từng là Thị trưởng thành phố, nhưng lúc Johannes ra đời, gia đình đang rơi vào cảnh khánh kiệt. Kepler là con cả trong số 7 người con của mẹ ông, nhưng ba trong số đó chết yểu. Người cha kiếm sống bấp bênh với nghề lính đánh thuê, rời bỏ gia đình khi Johannes mới năm tuổi và về sau được cho là đã chết trong Chiến tranh tám mươi năm ở Hà Lan. Mẹ ông, con gái một chủ quán trọ, là một thầy thuốc chữa bệnh bằng thảo dược và về sau bị kết án là phù thủy. Do đẻ non, Johannes từ bé đã yếu ớt và hay ốm đau nhưng bù lại cậu thông minh hơn người và người ta kể lại rằng khi còn nhỏ, cậu thường làm những khách trọ ở nhà ông ngoại ngạc nhiên vì khả năng toán học kỳ lạ của mình.[9]
Kepler làm quen với Thiên văn học từ rất sớm và gắn bó với nó trong cả cuộc đời. Năm 1577, khi mới lên sáu, cậu đã quan sát một siêu sao chổi, và sau này kể lại rằng cậu đã "được mẹ đưa lên một chỗ cao để nhìn nó".[10] Năm 1580, Kepler quan sát một hiện tượng thiên văn khác - nguyệt thực, cậu nhớ là đã "được gọi ra ngoài" để nhìn nó và rằng Mặt Trăng "có vẻ khá đỏ".[10] Tuy nhiên bệnh đậu mùa thời trẻ đã giảm thị lực và liệt tay của Kepler, khiến cậu bé phải chú tâm tới toán học nhiều hơn là quan sát các khía cạnh thiên văn học.[11]
Năm 1589, sau khi học qua trường văn phạm, trường tiếng Latinh, và chủng viện ở Maulbronn theo hệ thống giáo dục Lutheran, Kepler bắt đầu theo học tại Đại học Tübingen. Tại đây ông học triết học từ Vitus Müller[12] và thần học từ Jacob Heerbrand (một học trò của Philipp Melanchthon ở Wüttenberg người sau trở thành hiệu trưởng của trường.[13]. Kepler sớm chứng tỏ là một nhà toán học xuất chúng và nổi tiếng có tài chiêm tinh. Dưới sự hướng dẫn của giáo sư toán học Michael Maestlin[13], ông nghiên cứu cả hệ thống Ptolemy và hệ thống Copernicus về chuyển động hành tinh và trở thành một người ủng hộ Copernicus từ lúc đó. Trong một buổi tranh luận của sinh viên, Kepler đã lên tiếng bảo vệ thuyết nhật tâm cả từ quan điểm lý thuyết lẫn thần học, khẳng định rằng Mặt Trời là nguồn năng lượng chính cung cấp hoạt năng trong vũ trụ.[14]. Dù muốn trở thành một mục sư, gần cuối thời gian học, Kepler được tiến cử vào vị trí giáo viên toán và thiên văn học tại trường Tin Lành ở Graz, Áo. Ông nhận vị trí đó vào tháng 4, 1594, lúc 23 tuổi.[15]
Khởi đầu sự nghiệp (1594–1600)
[sửa | sửa mã nguồn]Mysterium Cosmographicum
[sửa | sửa mã nguồn]
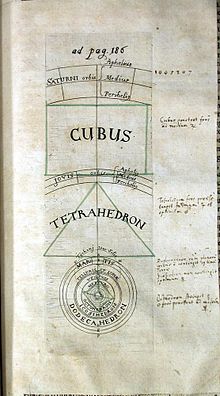
Tại Graz, Kepler bắt đầu phát triển một lý thuyết bảo vệ hệ thống Copernicus, xuất bản năm 1596 với tên Mysterium Cosmographicum—(Bí ẩn vũ trụ). Ông tuyên bố là đã có một thị kiến vào ngày 19 tháng 7 năm 1595 chứng minh sự giao hội của Sao Mộc và Sao Thủy trên hoàng đạo; ông nhận ra rằng các đa giác đều nội tiếp và ngoại tiếp đường tròn theo những tỉ lệ xác định, mà theo lập luận của ông, có thể là những cơ sở hình học của vũ trụ. Sau khi thất bại trong việc tìm một cách sắp xếp duy nhất các đa giác cho khớp với quan trắc thiên văn (ngay cả khi cho thêm vào ba hành tinh), Kepler bắt đầu thí nghiệm với những hình khối đa diện ba chiều. Ông thấy rằng các khối đa diện đều Platon có thể nội tiếp và ngoại tiếp bởi các khối cầu tròn; lồng những khối đa diện này với nhau, mỗi khối giới hạn bởi một khối cầu, kết quả là ta có sáu lớp, tương ứng với sáu hình tinh được biết đến thời đó - Sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ. Bằng cách sắp xếp các khối đa diện theo thứ tự-hình 8 mặt, hình 20 mặt, hình 12 mặt, hình 4 mặt (tứ diện), hình lập phương-Kepler thấy rằng các khối cầu có thể đặt vào các khoảng tương ứng (trong giới hạn chính xác của quan trắc thiên văn đương thời) với kích thước tương đối của quỹ đạo của mỗi hành tinh, với giả thiết là chúng quay xung quanh Mặt Trời. Kepler cũng tìm thấy công thức liên hệ giữa kích thước của khối cầu ứng với mỗi hành tinh và chu kỳ quỹ đạo của nó: từ hành tinh phía trong tới hành tinh phía ngoài, tỉ lệ sự tăng chu kỳ quỹ đạo gấp đôi tỉ lệ giữa bán kính khối cầu. Tuy nhiên, Kepler về sau từ bỏ công thức này, vì nó chưa được chính xác.[16]

Như tên gọi cuốn sách phần nào chỉ ra, Kepler nghĩ rằng ông đã phát lộ kế hoạch thiết lập vũ trụ có tính hình học của Thượng đế. Phần lớn nhiệt huyết của Kepler đối với hệ thống Copernicus bắt nguồn từ xác tín thần học của ông về mối liên hệ giữa cái Vật chất và cái Tinh thần; vũ trụ tự nó là một hình ảnh của Chúa, với Mặt Trời ứng với Chúa Cha, thiên cầu ứng với Chúa Con, và không gian ở giữa ứng với Chúa Thánh Linh. Bản thảo đầu tiên của Mysterium còn có một chương mở rộng nhằm hòa giải thuyết nhật tâm với các trích đoạn Kinh Thánh vốn dường như ủng hộ thuyết địa tâm.[17]
Với sự giúp đỡ của thầy hướng dẫn là Michael Maestlin, Kepler nhận được hội đồng trường Đại học Tübingen cho phép xuất bản bản thảo, trong lúc chờ để chỉnh sửa, loại bỏ phần chú giải Kinh Thánh và thêm vào một đoạn mô tả đơn giản, dễ hiểu hơn hệ thống Copernicus cũng như những ý tưởng mới của Kepler. Mysterium mãi đến năm 1596 mới được in, và đầu năm 1597 Kepler nhận các bản in để gửi cho những nhà thiên văn và nhà bảo trợ có tiếng; nó không được truyền bá rộng rãi, nhưng ít nhất đã tạo dựng danh tiếng một nhà thiên văn xuất chúng cho Kepler. Những lời đề tặng hoa mỹ, dành cho những nhà bảo trợ quyền lực cũng như những người kiểm soát vị trí của ông ở Graz, cũng đem lại một lối đi thiết yếu tới hệ thống bảo trợ.[18]
Mặc dù các công trình sau này có sửa chữa nhiều chi tiết của cuốn sách, Kepler không bao giờ đoạn tuyệt vũ trụ học đa diện đều-khối cầu trong Mysterium Cosmographicum. Các công trình thiên văn quan trọng của ông về sau ít nhiều có thể được coi như sự phát triển rộng thêm của nó, liên quan tới việc tìm các kích thước chính xác hơn cho các khối cầu bằng cách tính toán tâm sai của các quỹ đạo hành tinh bên trong chúng. Năm 1621 Kepler tái bản Mysterium dài gấp rưỡi ấn bản đầu tiên, với các cước chú mô tả chi tiết các hiệu chỉnh và cải tiến mà ông đạt được sau 25 năm.[19]
Nói về ảnh hưởng của Mysterium, nó có thể được xem như là bước quan trọng đầu tiên trong việc hiện đại hóa lý thuyết đề xuất bởi Nicolaus Copernicus trong tác phẩm "De Revolutionibus". Trong khi Copernicus tìm cách giới thiệu một hệ thống nhật tâm, ông tinh chỉnh các công cụ toán học của Ptolemaeus (tức ngoại luân và các đường tròn lệch tâm) để giải thích sự thay đổi tốc độ chuyển động quay của hành tinh, và đồng thời tiếp túc sử dụng tâm quỹ đạo Trái Đất như một điểm quy chiếu thay vì Mặt Trời "như một sự hỗ trợ cho tính toán và để tránh làm độc giả nhầm lẫn khi chệch quá xa khỏi đường hướng của Ptolemaeus." Thiên văn học hiện đại nợ "Mysterium Cosmographicum" rất nhiều, bất chấp những sai lầm trong luận đề chính của nó, "bởi vì nó đại diện cho bước đầu tiên tẩy trừ những tàn dư của lý thuyết Ptolemaeus vẫn còn bám lấy hệ thống Copernicus."[20]
Kết hôn với Barbara Müller
[sửa | sửa mã nguồn]
Tháng 12 năm 1595, Kepler làm quen với Barbara Müller, một góa phụ 23 tuổi đã qua 2 đời chồng và có một con gái nhỏ, Gemma van Dvijneveldt, và họ bắt đầu hẹn hò. Müller, người thừa kế điền sản của những người chồng quá cố, cũng là con gái của một nhà chủ cối xay thành đạt. Cha cô Jobst ban đầu phản đối bất chấp dòng dõi của Kepler; dù ông thừa hưởng tên tuổi của ông nội, sự nghèo túng của Kepler khiến cho cuộc hôn nhân có vẻ không môn đăng hộ đối. Những lần Kepler viếng thăm nhà Müller rất ít ỏi và bị đón tiếp lạnh nhạt, tuy nhiên những người mai mối đã vận động tích cực cho Kepler. Ngay cả vậy, lễ đính ước chỉ suýt chút nữa là hủy bỏ nếu những vị giáo chức không gây áp lực lên nhà Müller yêu cầu tôn trọng thỏa thuận. Barbara và Johannes cuối cùng kết hôn vào ngày 27 tháng 4, 1597.[21]
Trong những năm đầu cuộc hôn nhân, gia đình Kepler đã có hai đứa trẻ (tên là Heinrich và Susana), nhưng đều chết yểu. Năm 1602, họ có một đứa con gái (cũng lấy tên Susanna); và sau đó là hai con trai (Friedrich, 1604; Ludwig, 1607). Kepler cũng dành tình yêu mến cho con gái riêng Regina của Barbara.[22]
Các nghiên cứu khác
[sửa | sửa mã nguồn]Tiếp theo việc xuất bản Mysterium và với sự che chở của thanh tra trường Graz, Kepler bắt đầu một chương trình tham vọng nhằm mở rộng và trau chuốt công trình của mình. Ông đã dự định viết thêm 4 cuốn sách: một về các khía cạnh tĩnh tại của vũ trụ (Mặt Trời và các định tinh), một về các hành tinh và chuyển động của chúng, một về bản chất vật lý của các hành tinh và sự hình thành các đặc điểm địa lý (tập trung chủ yếu vào Trái Đất) và một về các tác động của bầu trời lên Trái Đất, bao gồm quang học khí quyển, khí tượng học và chiêm tinh học.[23]
Ông cũng tìm hiểu ý kiến của nhiều nhà thiên văn khác mà ông đã gửi tặng Mysterium, trong đó có Reimarrus Ursus-nhà toán học triều đình của Rudolf II và là một đối thủ kình địch với Tycho Brahe. Ursus không trả lời trực tiếp, nhưng cho in lá thư tâng bốc của Kepler để phục vụ cho cuộc tranh cãi quyền tác giả với Tycho (về thứ mà ngày nay được biết đến dưới tên hệ thống Tycho). Bất chấp tai tiếng này, Tycho cũng bắt đầu liên lạc với Kepler, khởi đầu một sự phê phán khắc nghiệt nhưng chính thống về hệ thống Kepler; trong một loạt những phản đối, Tycho không tán thành với việc sử dụng những dữ liệu số thiếu chính xác Kepler lấy từ Copernicus. Thông qua thư từ, Tycho và Kepler thảo luận những vấn đề rộng lớn hơn về thiên văn học, đặc biệt về các hoạt động của Mặt Trăng và lý thuyết Corpenicus (nhất là tính hợp lý về mặt thần học của nó). Nhưng không có những số liệu từ những quan sát của Tycho vốn chính xác hơn nhiều, Kepler không có cách nào giải quyết nhiều trong số vấn đề trên.[24]
Thay vào đó, ông chuyển sự quan tâm sang niên đại học và nghiên cứu về sự "hài hòa", hay quan hệ thần số học giữa âm nhạc, toán học, và thế giới vật lý, cũng như các ý nghĩa chiêm tinh có thể rút ra từ đó. Bằng cách giả thiết rằng Trái Đất có một linh hồn (một thuộc tính mà về sau ông viện chứng để giải thích cách Mặt Trời gây ra chuyển động của các hành tinh), ông thiết lập một hệ thống ước đoán liên kết các góc chiêm tinh và các khoảng cách thiên văn với thời tiết và các hiện tượng trên Trái Đất khác. Tuy nhiên tới năm 1599, ông lại một lần nữa cảm thấy công trình của mình bị hạn chế bởi tính thiếu chính xác của các dữ liệu hiện có, cũng như mối căng thẳng tôn giáo gia tăng đe dọa chỗ làm của ông ở Graz. Tháng 12 năm đó, Tycho mời Kepler đến thăm Praha; vào ngày 1 tháng 1 năm 1600 (trước cả khi nhận được lời mời), Kepler khởi hành với hi vọng rằng sự bảo trợ của Tycho sẽ giải quyết được những vấn đề của ông, cả về triết lý lẫn xã hội và tài chính.[25]
Nhà toán học hoàng gia ở Praha (1601–1612)
[sửa | sửa mã nguồn]Làm việc cho Tycho Brahe
[sửa | sửa mã nguồn]
Ngày 4 tháng 2 năm 1600, Kepler gặp Tycho Brahe và các trợ lý của ông là Franz Tengnagel và Longomontanus tại Benátky nad Jizerou (cách Praha 35 km), nơi đài thiên văn mới của Tycho đang được xây dựng. Hai tháng sau đó ông lưu lại như một vị khách, phân tích một vài số liệu của Tycho về Sao Hỏa; Tycho canh giữ dữ liệu của mình rất cẩn thận, nhưng rất ấn tượng với những ý tưởng lý thuyết của Kepler và dần cho phép ông được tiếp cận nhiều hơn. Kepler dự định kiểm chứng lý thuyết của mình[26] trong Mysterium Cosmographicum dựa trên dữ liệu Sao Hỏa, nhưng ông đánh giá rằng công trình có thể tốn đến hai năm (vì ông không được phép chép lại dữ liệu để dùng). Với sự giúp đỡ của Johannes Jessenius, Kepler tìm cách thỏa thuận một chỗ làm chính thức với Tycho, nhưng chuyện này đổ bể sau một cuộc tranh cãi nóng nảy và Kepler rời Praha ngày 6 tháng 4. Hai người sau đó sớm hòa giải và cuối cùng đi đến một thỏa thuận về lương bổng cũng như chỗ ăn ở, vào tháng 6, Kepler trở về nhà ở Graz để dọn cả gia đình tới Praha.[27]
Những khó khăn về tôn giáo và chính trị tại Graz dập tắt hi vọng chuyển nhà nhanh chóng của Kepler; trong nỗ lực tìm cách tiếp tục việc nghiên cứu thiên văn, Kepler thử xin được bổ nhiệm vào vị trí nhà toán học cho Đại công tước Ferdinand của Áo. Vì mục đích đó, ông đã viết một luận văn-đề tặng cho Ferdinand-trong đó ông đề xuất một lý thuyết giải thích chuyển động Mặt Trăng bằng lực: "In Terra inest virtus, quae Lunam ciet" (Có một lực trên Trái Đất khiến cho Mặt Trăng chuyển động).[28] Dù luận văn không mang lại cho ông một vị trí tại cung đình của Ferdinant, nó đã giúp vạch ra một phương pháp mới để đo đạc nguyệt thực mà ông dùng trong lần nguyệt thực ngày 10 tháng 7 tại Graz. Những quan sát này tạo nên cơ sở cho những khám phá của ông về các định luật quang học sau này sẽ kết tinh trong Astronomiae Pars Optica.[29]
Ngày 2 tháng 8, sau khi từ chối cải sang Công giáo, Kepler và gia đình bị trục xuất khỏi Graz. Vài tháng sau, Kepler đưa cả gia đình tới Praha. Trong suốt năm 1601, ông được Tycho hỗ trợ trực tiếp, giao cho ông việc phân tích các quan sát về hành tinh và viết một đoản luận chống lại Ursus (đã quá cố). Vào tháng 9, Tycho đảm bảo cho ông một vị trí cộng tác viên trong một dự án mới mà ông đề xuất với hoàng đế: Bảng Rudolf thay thế cho danh mục sao trước đây của Erasmus Reinhold. Hai ngày sau cái chết đột ngột của Tycho vào ngày 24 tháng 10 năm 1601, Kepler được bổ nhiệm làm người kế nhiệm ở vị trí nhà toán học hoàng gia với trách nhiệm hoàn thành những công trình dang dở của Tycho. Đã có những giả thiết rằng Kepler đầu độc Tycho để hưởng lợi[30] nhưng một nghiên cứu khai quật tử thi xác nhận rằng đó là đột tử do suy thận.[31] 11 năm làm nhà thiên văn hoàng gia từ đó sẽ là những năm nghiên cứu sôi nổi nhất cuộc đời ông.[32]
Cố vấn cho Hoàng đế Rudolf II
[sửa | sửa mã nguồn]Trách nhiệm chính của Kepler trong vai trò nhà toán học triều đình là cung cấp các phép bói chiêm tinh cho hoàng đế. Mặc dù Kepler lấy làm bi quan về những nỗ lực của các nhà chiêm tinh đương thời muốn tiên đoán chính các sự kiện cụ thể trong tương lai hoặc thuộc về thánh thần, chính ông cũng đã lấy nhiều lá số tử vi cho bạn bè, gia đình và những người bảo trợ ngay từ hồi còn học ở Tübingen và được đón nhận nồng hậu. Bên cạnh những lá số tử vi về các liên minh và các lãnh đạo nước ngoài, hoàng đế còn tìm lời chỉ dẫn từ Kepler về các vấn đề chính trị. Rudolf cũng tích cực quan tâm tới các công trình của các học giả ngụ tại triều đình của mình (nhiều trong số đó là các nhà giả kim thuật) và cũng để tâm tới nghiên cứu thiên văn học của Kepler.[33]
Về mặt chính thức, chỉ có Công giáo và phái Calixtine (nhánh ôn hòa của giáo hội cải cách Hussite) là những tín điều được công nhận ở Praha, tuy nhiên vị trí quan trọng của Kepler tại triều đình cho phép ông thực hành các nghi thức tôn giáo Lutheran mà không phải giấu diếm. Hoàng đế cung cấp một khoản thu nhập đáng kể trên danh nghĩa cho ông, nhưng những khó khăn do ngân khố quá tải của triều đình khiến cho các khoản lương không được thanh toán đầy đủ. Một phần vì các khó khăn tài chính, cuộc sống ở gia đình với người vợ Barbara không dễ dàng, chất đầy những tranh cãi vặt và những lần ốm đau. Tuy nhiên đời sống cung đình cho phép Kepler gặp gỡ với nhiều học giả nổi tiếng đương thời (trong đó có nhà ngoại giao, nhà triết học Wacker von Wackenfels, nhà thiên văn David Fabricius, nhà toán học Jost Burgi,...) cũng như có thể tiến hành các nghiên cứu thiên văn một cách thuận lợi.[34]
Astronomiae Pars Optica
[sửa | sửa mã nguồn]
Trong lúc ông dần dần phân tích số liệu quan sát Sao Hỏa của Tycho-giờ nằm hoàn toàn trong tay ông-và bắt đầu quá trình lập Bảng Rudolf một cách chậm chạp, Kepler cũng tiến hành hành nghiên cứu các định luật về quang học từ luận văn về Mặt Trăng của ông năm 1600. Cả nhật thực và nguyệt thực đều gây ra những hiện tượng chưa được giải thích, như những kích thước bóng kì lạ, màu đỏ máu của nguyệt thực toàn phần, và ánh sáng bất thường bao phủ nhật thực toàn phần. Các vấn đề liên quan tới khúc xạ trong khí quyển áp dụng tới mọi quan sát thiên văn. Trong gần như cả năm 1603, Kepler tạm dừng các công trình khác để tập trung vào lý thuyết quang học, và kết quả là một bản thảo được trình bày cho hoàng đế vào ngày 1 tháng 1 năm 1604, sau đó in dưới tên Astronomiae Pars Optica (tạm dịch: Một phần trong quang học thiên văn). Trong cuốn sách, Kepler mô tả định luật nghịch đảo bình phương về cường độ ánh sáng, sự phản xạ bởi gương phẳng và gương cong, và các nguyên lý của máy ảnh lỗ kim (pinhole camera, tức máy ảnh không có ống kính, dùng để quan sát nhật thực), cũng như những ngụ ý thiên văn học của quang học như thị sai và kính thước biểu kiến của các thiên thể. Ông cũng mở rộng nghiên cứu về quang học sang mắt người, và do đó các nhà khoa học thần kinh ghi nhận Kepler là người đầu tiên nhận ra rằng hình ảnh được chiếu lộn ngược vào mắt nhờ có thấu kính mắt (thủy tinh thể) lên võng mạc. Kepler dường như không coi trọng giải đáp vấn đề này cho lắm vì ông không cho nó liên quan tới cơ học, nhưng ông đã gợi ý rằng hình ảnh sau đó được hiệu chỉnh trong những "chỗ rỗng của bộ não" do "những hoạt động của Linh hồn", một nhận xét mang tính tiên tri về thần kinh thị giác.[35] Ngày nay, Astronomiae Pars Optica thường được xem là nền tảng của quang học hiện đại (dù cho định luật khúc xạ còn chưa được biết tới).[35] Kepler cũng đóng góp cho sự hình thành của hình học xạ ảnh với việc giới thiệu ý tưởng về sự thay đổi liên tục của một thực thể toán học trong công trình này. Ông lập luận rằng nếu một tiêu điểm của một đường cô-nic được phép di chuyển dọc theo được thẳng nối các tiêu điểm, dạng hình học sẽ thay đổi hoặc suy biến thành một dạng khác. Theo cách này, một elip sẽ biến thành parabol khi một tiêu điểm tiến tới vô cùng, và khi hai tiêu điểm của một elip nhập thành một, một đường tròn sẽ xuất hiện. Khi hai tiêu điểm của một hyperbol sáp nhập với nhau, hyperbol sẽ biến thành một cặp đường thẳng. Ông cũng giả thiết rằng nếu một đường thẳng được mở rộng tới vô cực nó sẽ gặp chính nó tại một điểm tại vô cực duy nhất, và do đó có những tính chất của một đường tròn bán kính vô cùng lớn. Ý tưởng này về sau được nhiều nhà toán học như Pascal, Leibniz, Monge và Poncelet vận dụng, và được biết dưới tên "tính liên tục hình học" hay định luật về tính liên tục.[36]
Siêu tân tinh năm 1604
[sửa | sửa mã nguồn]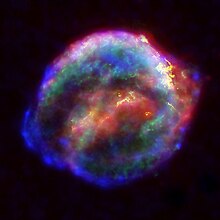
Tháng 10 năm 1604, một ngôi sao mới rất sáng xuất hiện lúc chập tối, nhưng Kepler không tin vào những tin đồn cho tới khi ông tận mắt nhìn thấy. Kepler bắt đầu quan sát một cách hệ thống tinh vân đó. Theo chiêm tinh học, cuối năm 1603 đánh dấu sự khởi đầu của một tam giác lửa (tam giác hướng lên là biểu tượng của lửa trong chiêm tinh), bắt đầu cho một chu kỳ 800 năm của các đại giao hội; các nhà chiêm tinh liên kết hai chu kỳ trước với sự nổi lên của Charlemagne và sự ra đời của Jesus, và do đó trông đợi những điềm báo lớn, đặc biệt là liên quan tới hoàng đế. Chính trong hoàn cảnh này, với tư cách nhà toán học triều đình và nhà chiêm tinh cho hoàng đế, Kepler mô tả ngôi sao mới hai năm sau đó trong cuốn De Stella Nova. Trong đó Kepler mô tả các đặc điểm thiên văn về ngôi sao trong khi giữ một cách tiếp cận hoài nghi đối với nhiều cách diễn giải chiêm tinh về nó lưu hành đương thời. Ông ghi chép về độ sáng giảm dần của sao, phỏng đoán về nguồn gốc của nó, và sử dụng sự không quan sát thấy quang sai để lập luận rằng nó nằm trong vòm cầu các định tinh, từ đó làm xói mòn thêm giáo điều về tính bất biến của thiên giới (ý tưởng có từ thời Aristotle rằng các thiên cầu là hoàn hảo và bất biến). Sự ra đời của một ngôi sao mới ngụ ý tính có thể thay đổi của thiên giới. Trong một phụ lục, Kepler cũng thảo luận về một công trình niên đại học mới hồi đó của nhà sử học Ba Lan Laurentius Suslyga; ông tính toán rằng, nếu Suslyga chính xác khi nói những niên biểu được chấp nhận thời bấy giờ bị chậm 4 năm, thì Ngôi sao Bethlehem-tương đồng với ngôi sao mới hiện tại-sẽ trùng hợp với đại giao hội lần thứ nhất của chu kỳ 800 năm trước đó.[37]
Astronomia nova
[sửa | sửa mã nguồn]Dòng nghiên cứu mở rộng đúc kết trong Astronomia nova (Một Thiên văn học mới)-bao gồm hai định luật đầu về chuyển động hành tinh-bắt đầu với phân tích, dưới sự chỉ dẫn của Tycho, về quỹ đạo Sao Hỏa. Kepler tính toán lại nhiều phép xấp xỉ khác nhau về quỹ đạo Sao Hỏa sử dụng một đẳng thước (công cụ toán học mà Copernicus phê phán và loại bỏ khỏi công trình của ông), cuối cùng tạo nên một mô hình nhìn chung phù hợp với quan sát của Tycho trong sai số đo đạc trung bình khoảng 2 phút. Nhưng ông cảm thấy chưa hài lòng với kết quả phức tạp và vẫn ít nhiều không khớp này; ở một số điểm mô hình chênh lệch với dữ liệu tới 8 phút. Hàng loạt các phương pháp thiên văn toán học truyền thống không đáp ứng được ông, và Kepler bắt đầu thử quy hồi một quỹ đạo hình trứng với dữ liệu.[38]
Trong quan điểm thần học của Kepler về vũ trụ, Mặt Trời (một biểu tượng của Chúa Cha) là nguồn của các hoạt lực trong Hệ Mặt Trời. Kepler vạch ra một cơ sở vật lý cho nó, tương đồng với lý thuyết của William Gilbert về linh hồn từ tính của Trái Đất trong cuốn De Magnete (1600) và công trình của chính ông về quang học, Kepler giả thiết rằng hoạt lực (hay loại chuyển động trong phân loại Aristotle)[39] phát ra từ Mặt Trời suy yếu theo khoảng cách, khiến cho các hành tinh chuyển động nhanh hơn khi tiến tới gần Mặt Trời và chậm hơn khi rời xa nó.[40][41] Có lẽ giả thiết này đưa đến một mối liên hệ toán học sẽ khôi phục trật tự thiên văn học. Dựa trên các đo đạc về các điểm viễn nhật và cận nhật của Trái Đất và Sao Hỏa, ông lập nên một công thức trong đó tốc độ chuyển động của một hành tinh tỷ lệ nghịch với khoảng cách từ nó tới Mặt Trời. Tuy nhiên việc kiểm tra quan hệ này trong suốt chu kỳ quỹ đạo, cần số lượng vô cùng lớn những phép tính toán; để đơn giản hóa nhiệm vụ này, cuối năm 1602 Kepler thiết lập lại tỉ lệ bằng hình học: các hành tinh quét những diện tích bằng nhau trong các khoảng thời gian bằng nhau-đó chính là định luật thứ hai của Kepler về chuyển động hành tinh.[42]

Sau đó ông bắt đầu tính toán toàn bộ quỹ đạo của Sao Hỏa, sử dụng định luật tỉ lệ hình học và giả thuyết một quỹ đạo hình trứng. Sau khoảng 40 lần thất bại, cuối cùng vào đầu năm 1605 ông đã đi đến ý tưởng về một quỹ đạo elip, mà trước đó ông cho là quá đơn giản, không thể nào các nhà thiên văn trước đó lại bỏ qua được (!). Phát hiện ra rằng một quỹ đạo elip khớp với dữ liệu về Sao Hỏa, ông lập tức kết luận rằng tất cả mọi hành tinh chuyển động theo các đường elip, với Mặt Trời nằm ở một tiêu điểm-đó là định luật thứ nhất của Kepler về chuyển động hành tinh. Tuy nhiên bởi không sử dụng một phụ tá nào để tính toán, ông không thể mở rộng phân tích toán học ra ngoài Sao Hỏa. Cuối năm đó, ông hoàn thành bản thảo của Astronomia nova, nhưng phải đợi tới năm 1609 mới xuất bản được do các tranh cãi pháp lý liên quan tới việc sử dụng dữ liệu quan sát của Tycho với những người thừa kế trong dòng họ Brahe.[43]
Dioptrice, bản thảo Somnium và các công trình khác
[sửa | sửa mã nguồn]Những năm sau khi hoàn thành Astronomia Nova, hầu hết nghiên cứu của Kepler tập trung vào việc chuẩn bị các bảng Rudolf và một tập hợp các lịch thiên văn dựa trên bảng đó. Ông cũng thử bắt đầu một sự hợp tác với nhà thiên văn người Ý Giovanni Antonio Magini, nhưng bất thành. Một vài công trình khác của ông liên quan tới niên đại học, đặc biệt là những sự kiện trong cuộc đời Jesus, và chiêm tinh học, chủ yếu là sự phê phán các tiên đoán hão huyền về các thảm họa diệt vong như của Helisaeus Roeslin.[44]
Kepler và Roeslin đụng độ nhau trong một loài những bài tấn công ăn miếng trả miếng, trong khi bác sĩ Philip Feselius công bố một công trình phản bác môn chiêm tinh nói chung, nhất là công trình của Roeslin. Đáp lại cái mà Kepler cho là sự thái quá của một bên là chiêm tinh học và bên kia là sự chối bỏ nó quá hăng hái, Kepler soạn Tertius Interveniens (tạm dịch: Những can thiệp từ bên thứ ba). Về danh nghĩa công trình này - được giới thiệu cho nhà bảo trợ chung của Roeslin và Feselius-là một suy nghĩ giảng hòa giữa các học giả thù nghịch, nhưng nó cũng trình bày quan niệm chung Kepler về giá trị của chiêm tinh học, bao gồm một vài cơ chế có tính giả thuyết về tương tác giữa hành tinh và linh hồn con người. Trong khi Kepler xem hầu hết các phương pháp và quy tắc truyền thống của chiêm tinh học là "phân dậy mùi quỷ dữ" trong đó một con gà cần mẫn kéo lê chân, có một "hạt giống hiếm hoi, thực vậy, thậm chí một hạt ngọc trai hay cục vàng" có thể tìm thấy bằng những nhà chiêm tinh khoa học ngay thẳng.[45]

Đầu năm 1610, Galileo Galilei sử dụng kính viễn vọng do ông mới chế tạo, đã khám phá ra 4 hành tinh quay quanh Sao Mộc. Vào lúc công bố phát hiện của mình (tức quyển Sidereus Nuncius-Sứ giả Sao), Galileo tham khảo ý kiến của Keler, một phần để nhằm tăng cường uy tín cho những quan sát của mình. Kepler trả lời một cách nồng nhiệt bằng một tiểu luận ngắn được in dưới tên Dissertatio cum Nuncio Sidereo (tạm dịch: Thảo luận với Sứ giả Sao). Ông xác nhận quan sát của Galileo và đưa ra một loạt phỏng đoán về ý nghĩa và ngụ ý của các khám phá và phương pháp dùng kính viễn vọng của Galileo, cho thiên văn học cũng như vũ trụ học, chiêm tinh học. Sau đó vào cùng năm Kepler công bố các kết quả quan sát dùng kính viễn vọng của chính mình về các mặt trăng đó trong Narratio de Jovis Satellitibus (tạm dịch, Mô tả về các vệ tinh Sao Mộc), cung cấp thêm sự ủng hộ cho Galileo. Tuy nhiên Galileo đã gây thất vọng cho Kepler khi không bao giờ công bố những phản hồi (nếu có) về Astronomia Nova.[47]
Sau khi nghe nói về khám phá về kính viễn vọng của Galileo, Kepler cũng bắt đầu những nghiên cứu cả lý thuyết và thực nghiệm về quang học viễn vọng sử dụng một kính viễn vọng mượn từ Công tước Ernest của Cologne.[48] Bản thảo hoàn thành tháng 9 năm 1610 và công bố dưới tên Dioptrice (Khúc xạ học) năm 1611. Trong đó, Kepler thiết lập cơ sở lý thuyết của các thấu kính hội tụ lồi kép và thấu kính phân kỳ lõm kép-và cách chúng kết hợp để tạo nên kính viễn vọng của Galileo-cũng như quan niệm về ảnh thực và ảnh ảo, ảnh đứng và ảnh ngược, và ảnh hưởng của tiêu cự lên độ phóng đại và độ thu nhỏ. Ông cũng mô tả một kính viễn vọng cải tiến-ngày nay được gọi là kính thiên văn Kepler-trong đó hai thấu kính lồi có thể tạo ra độ phóng đại lớn hơn tổ hợp thấu kính lồi và lõm của Galileo.[49]

Vào khoảng năm 1611, Kepler cho lưu hành một bản thảo của tiểu thuyết Somnium (Giấc mơ, được con trai Kepler in sau khi ông mất). Một phần mục đích của Somnium là để mô tả việc thực hành thiên văn sẽ như thế nào từ góc nhìn ở một hành tinh khác, để chỉ ra tính tiện lợi của một hệ thống phi địa tâm. Bản thảo, đã biến mất sau khi trao tay một vài lần, mô tả một chuyến đi tưởng tượng tới Mặt Trăng, nó một phần mang tính phóng dụ, một phần mang tính tự truyện, và một phần có tính luận văn về du hành liên hành tinh (Carl Sagan lẫn Isaac Asimov xem đây là tiểu thuyết khoa học viễn tưởng đầu tiên trong lịch sử[50]). Nhiều năm về sau, một phiên bản bóp méo của câu chuyện xét tới phiên tòa buộc tội mẹ ông là phù thủy, với người mẹ là người dẫn truyện tham vấn một con quỷ để học cách du hành ngoài không gian. Sau khi bà cuối cùng được tha bổng, Kepler sáng tác thêm 223 cước chú cho câu chuyện-dài gấp vài lần bản thân văn bản gốc-để diễn giải những khía cạnh phúng dụ cũng như nội dung khoa học đáng kể (đặc biệt là đề cập tới địa lý trên Mặt Trăng) ẩn chứa trong văn bản.[51]
Như một món quà năm mới, trong năm 1611 ông cũng sáng tác một tiểu luận tựa đề Strena Seu de Nive Sexangula (tạm dịch, Một món quà Năm Mới về Tuyết Lục giác). Trong luận văn này, Kepler đã lần đầu tiên mô tả đối xứng lục giác của bông tuyết, thảo luận về một cơ sở vật lý nguyên tử luận có tính giả thiết cho đối xứng, và đề xuất thứ sau này được biết tới như Giả thiết Kepler, một mệnh đề về sự sắp xếp tối ưu các khối cầu đặc[52][53]
Các vấn đề chính trị và đời sống cá nhân
[sửa | sửa mã nguồn]Năm 1611, căng thẳng tôn giáo-chính trị Praha trở thành một cuộc khủng hoảng thực sự. Hoàng đế Rudolf-khi đó sức khỏe đang suy yếu-bị em trai là Matthias buộc nhường tước hiệu vua Bohemia. Cả hai phe đều tìm lời chỉ dẫn chiêm tinh của Kepler, một cơ hội mà ông đã sử dụng để đưa ra những lời khuyên chính trị mang tính hòa giải (mà ít khi liên hệ với các ngôi sao, trừ trong những khẳng định chung chung nhằm can ngăn những hành động vũ lực bộc phát). Nhưng rõ ràng viễn cảnh tương lai của Kepler trong triều đình Matthias là mờ nhạt.[54]
Cũng trong năm đó, vợ ông Barbara Kepler mắc bệnh sốt phát ban Hungary, và sau đó bắt đầu có những cơn động kinh. Khi Barbara hồi phục, cả ba đứa trẻ đều nhiễm đậu mùa, đứa con trai lớn, Friedrich, mất (6 tuổi). Sau cái chết của con trai, Kepler gửi thư tới các nhà bảo trợ tiềm năng ở Württemberg và Padua để tìm cơ hội di cư. Ở Đại học Tübingen (Württemberg), những lo ngại về việc Kepler đã tiếp nhận dị giáo Calvin vi phạm Tín điều Augsburg đã ngăn cản ông trở về. Tại Đại học Padua, Galileo lúc ấy sắp ra đi giới thiệu Kepler thay ghế giáo sư toán, tuy nhiên Kepler muốn gia đình sống trong lãnh thổ Đức đã không nhận lời; thay vào đó ông tới Áo để sắp xếp một vị trí giáo viên và nhà toán học của hạt Linz. Tuy nhiên, bệnh của Barbara tái phát và bà mất ít lâu sau khi Kepler về nhà.[55]
Kepler hoãn việc chuyển nhà và ở lại Praha cho tới khi Rudolf qua đời vào đầu năm 1612, mặc dù ông cũng không thể nghiên cứu được gì giữa những rối loạn chính trị, căng thẳng tôn giáo và bi kịch gia đình này. Thay vào đó, ông sắp xếp các thư từ và công trình trước đây về niên đại học thành tác phẩm Eclogae Chronicae (tức Tuyển tập niên đại học). Sau khi kế vị ngôi Hoàng đế Thánh chế La Mã, Matthias tái xác nhận vị trí nhà toán học triều đình (và lương bổng) của Kepler nhưng cho phép ông dời tới Linz.[56]
Dạy học ở Linz và những năm cuối đời (1612–1630)
[sửa | sửa mã nguồn]
Tại Linz, các công việc chính của Kepler (bên cạnh việc hoàn thành các Bảng Rudolf) là dạy tại trường của thành phố và cung cấp các dịch vụ chiêm tinh và thiên văn. Trong những năm đầu tiên ở đây, ông bớt bấp bênh về tài chính và được hưởng tự do tín ngưỡng hơn so với cuộc sống ở Praha—mặc dù giáo hội Luther trừng phạt sự không dứt khoát trong thần học của ông bằng việc không ban bí tích Thánh thể. Công trình đầu tiên ông công bố ở Linz là De vero Anno (1613), một luận văn bao quát về năm Chúa Giáng sinh, ông cũng tham gia vào cuộc bàn cãi về việc có nên ban bố lịch cải cách của Giáo hoàng Grêgôriô XII trên những vùng lãnh thổ Đức theo Kháng Cách hay không; cùng năm đó ông cũng viết một luận văn toán học quan trọng Nova stereometria doliorum vinariorum, về việc đo thể tích của các vật chứa như thùng rượu vang, xuất bản năm 1615.[57]
Kết hôn lần hai
[sửa | sửa mã nguồn]Ngày 30 tháng 10 năm 1613, Kepler làm đám cưới với cô gái 24 tuổi Susanna Reuttinger. Kề từ sau cái chết của người vợ đầu Barbara, Kepler đã cân nhắc kỹ lưỡng 11 người khác nhau trong vòng 2 năm (quá trình ra quyết định này được ông tối ưu trong đầu và về sau công thức hóa thành bài toán hôn nhân.[58] Ông cuối cùng quay trở lại với Reuttinger (đám mai mối thứ năm), người mà ông viết, "đã thu phục tôi với tình yêu, sự tận tụy khiêm tốn, khả năng quản lý kinh tế gia đình, tính siêng năng, và tình yêu dành cho con riêng."[59] Ba đứa trẻ đầu của cuộc hôn nhân thứ hai này (Margareta Regina, Katharina, và Sebald) đều chết yểu. Ba người con sau trưởng thành: Cordula (sinh năm 1621), Fridmar (1623), Hildebert (1625). Theo các nhà viết tiểu sử Kepler, đây là mối hôn nhân hạnh phúc hơn nhiều so với lần đầu.[60]
Epitome astronomiae Copernicanae, lịch biểu và phiên tòa xử mẹ ông
[sửa | sửa mã nguồn]Từ khi hoàn thành Astronomia nova, Kepler dự định viết một cuốn sách giáo khoa thiên văn học.[61] Năm 1615, ông hoàn thành tập đầu tiên trong ba tập của Epitome astronomiae Copernicanae (Tạm dịch: Thiên văn học Copernicus giản lược); tập đầu (các quyển I-III) được in năm 1617, tập hai (quyển IV) in năm 1617, và tập ba (các quyển V-VII) năm 1621. Trong khi tựa đề đơn thuần nhắc tới thuyết nhật tâm, thực tế cuốn sách giáo khoa này của Kepler hoàn thiện hệ thống dựa trên quỹ đạo elip của chính ông, và đã trở thành công trình gây ảnh hưởng nhất của ông. Nó chứa đựng toàn bộ ba định luật về chuyển động hành tinh và nỗ lực giải thích chuyển động thiên thể bằng những nguyên nhân vật lý.[62] Dù nó mở rộng rõ ràng hai định luật đầu của chuyển động hành tinh (từng áp dụng cho Sao Hỏa trong Astronomia nova) cho tất cả các hành tinh cũng như Mặt Trăng và các mặt trăng của Sao Mộc,[63] nó đã không giải thích làm thế nào các quỹ đạo elip có thể rút ra từ các dữ liệu quan sát.[64]
Như một sản phẩm phụ từ Bảng Rudolf và các lịch thiên văn, Kepler công bố các lịch chiêm tinh, rất phổ biến thời bấy giờ và giúp một phần trang trải chi phí cho các công trình khác của ông-đặc biệt là khi ngân khố triều đình từ chối hỗ trợ tài chính. Trong 6 tập lịch của ông những năm 1617-1624-Kepler đã dự đoán các vị trí hành tinh và thời tiết cũng như các sự kiện chính trị; thú vị là các dự đoán chính trị thường chính xác một cách cẩn trọng, có lẽ nhờ vào sự hiểu biết sắc sảo của Kepler về những mối căng thẳng chính trị và tôn giáo đương thời. Nhưng chính sự leo thang của những căng thẳng này và sự mập mờ trong những lời tiên tri đem lại rắc rối chính trị cho chính Kepler; tập lịch cuối cùng của ông (1624) bị đốt bỏ công khai ở Graz.[65]
Năm 1615, Ursula Reingold, một người đàn bà có tranh cãi tiền nong với em trai Kepler là Christoph, đã quả quyết rằng mẹ của Kepler, bà Katharina, đã làm cho bà ta ốm bằng một cốc bia của quỷ. Tranh cãi leo thang, và năm 1617 Katharina bị cáo buộc là phù thủy; các vụ xử phù thủy tương đối phổ biến ở trung Âu thời kỳ đó. Từ tháng 10 năm 1620, bà bị tống giam trong 14 tháng liền. Sau đó một phần nhờ những nỗ lực pháp đình của Kepler, Katharina được thả ra. Những kẻ buộc tội không có bằng chứng nào mạnh ngoài những tin đồn, cùng với một phiên bản xuyên tạc cuốn Somnium của Kepler, trong đó một người đàn bà trộn các liều thuốc độc và viện đến sự trợ giúp của một con quỷ. Katharina chịu territio verbalis, tức trình bày công cụ tra tấn để đe dọa và buộc bà thú tội. Trong suốt phiên xử, Kepler hoãn tất cả công việc khác, và chỉ dành thời gian cho "lý thuyết hài hòa" của ông. Kết quả của công trình này được công bố năm 1619, đó chính là Harmonices Mundi (Vũ trụ Hài hòa)[66]
Harmonices Mundi
[sửa | sửa mã nguồn]Kepler có niềm tin rằng "các vật thể hình học cho Đấng Sáng tạo mô hình để trang hoàng toàn thế giới".[67] Trong cuốn sách, ông nỗ lực thử giải thích những tỉ lệ hình học của thế giới tự nhiên-đặc biệt là các khía cạnh thiên văn và chiêm tinh-bằng âm nhạc.[68]. Tập hợp trung tâm của các "hài hòa" là musica universalis hay "âm nhạc của những khối cầu", một đề tài đã từng được Pythagoras, Ptolemaeus và nhiều người khác trước Kepler nghiên cứu; ngoài ra, ít lâu sau khi xuất bản sách, Kepler bị lôi vào một cuộc tranh cãi về quyền tác giả với Robert Fludd, người trước đó đã công bố lý thuyết hài hòa riêng của ông ta.[69]
Tác phẩm khởi đầu bằng việc khảo sát các đa giác đều và các khối đa diện đều, trong đó một số dạng hình học về sau được biết dưới tên khối đa diện Kepler. Từ đó, ông mở rộng phân tích tính hài hòa sang âm nhạc, khí tượng học và chiêm tinh học; hài hòa sinh ra từ những âm thanh của linh hồn các thiên thể-và trong trường hợp chiêm tinh học là tương tác giữa các âm thanh này và linh hồn con người. Trong phần cuối cùng của tác phẩm (quyển V), Kepler giải quyết vấn đề chuyển động hành tinh, đặc biệt là mối quan hệ giữa vận tốc quỹ đạo và khoảng cách quỹ đạo từ Mặt Trời. Các mối quan hệ tương tự cũng được các nhà thiên văn khác sử dụng, nhưng Kepler-với dữ liệu của Tycho và lý thuyết thiên văn của riêng ông-xử lý chúng chính xác hơn nhiều và gán ý nghĩa vật lý mới cho chúng.[70]
Trong số các hài hòa, Kepler phát biểu rõ ràng về cái sau này được xem là Định luật thứ ba về chuyển động hành tinh. Ông đã thử nhiều tổ hợp khác nhau trước khi khám phá ra rằng, một cách xấp xỉ, "Tỉ lệ bình phương của chu kỳ [của hai hành tinh] với nhau bằng tỉ lệ lập phương khoảng cách trung bình". Mặc dù ông có nêu ra ngày phát kiến ra điều này (8 tháng 3 năm 1618), ông lại không nói chi tiết cách ông đi đến kết luận.[71] Tuy nhiên, ý nghĩa rộng rãi hơn về động lực học thiên thể của định luật thuần túy động học này không được nhìn nhận cho tới những năm 1660. Chắp nối với định luật về lực hướng tâm mà Christiaan Huygens mới khám phá, nó cho phép Isaac Newton, Edmund Halley, và có lẽ cả Christopher Wren và Robert Hooke chứng minh độc lập với nhau rằng; lực hút trọng trường được giả thiết giữa Mặt Trời và các hành tinh giảm dần theo bình phương khoảng cách giữa chúng.[72] Điều này bác bỏ giả thiết truyền thống của vật lý kinh viện rằng tác dụng của sức hút giữ nguyên không đổi theo khoảng cách bất kể khi nào nó áp dụng giữa hai vật thể, như chính cách Kepler và cả Galileo, trong định luật vũ trụ sai lầm của ông, cho rằng sự rơi trong trọng trường được tăng tốc đều, cũng như học trò của Galileo là Borrelli trong một tác phẩm cơ học thiên thể năm 1666.[73] William Gilbert, sau khi thí nghiệm với nam châm, tuyên bố rằng tâm Trái Đất là một nam châm khổng lồ. Lý thuyết đó dẫn Kepler nghĩ rằng một lực từ Mặt Trời kéo các hành tinh theo quỹ đạo. Đó là một lối giải thích thú vị về chuyển động hành tinh, nhưng sai lầm do đương thời chưa có hiểu biết đầy đủ về chuyển động.[74]
Bảng Rudolf và những năm cuối cùng
[sửa | sửa mã nguồn]
Năm 1623, cuối cùng Kepler cũng hoàn thành Bảng Rudolf, mà sinh thời đó được xem là công trình chính của đời ông. Tuy nhiên, do những yêu cầu xuất bản của hoàng đế và những thương thảo với người thừa kế của Tycho Brahe, phải đến tận năm 1627 nó mới được in. Trong khi đó, những căng thẳng tôn giáo-nguồn gốc của Chiến tranh Ba mươi năm đang diễn ra bấy giờ-một lần nữa đẩy gia đình Kepler vào cảnh hiểm nghèo. Năm 1625, những thừa sai Phản Kháng Cách đến niêm phong phần lớn thư viện của Kepler, và năm 1626 thành phố Linz bị bao vây. Kepler dời tới Ulm, nơi ông tìm cách tự in Bảng Rudolf bằng tiền của mình.[75]
Năm 1628, theo sau những thắng lợi quân sự của quân đội Hoàng đế Ferdinand dưới quyền tướng Albrecht von Wallenstein, Kepler trở thành cố vấn chính thức cho Wallenstein. Mặc dù không phải là một nhà chiêm tinh thực sự cho vị tướng, Kepler cung cấp các tính toán thiên văn cho các nhà chiêm tinh của Wallenstein và thỉnh thoảng lập lá số tử vi. Trong những năm cuối cùng, Kepler thường xuyên du hành, từ triều đình ở Praha tới Linz và Ulm tới một ngôi nhà tạm ở Żagań, rồi cuối cùng tới Regensburg. Ít lâu sau khi tới Regensburg, Kepler đổ bệnh. Ông mất ngày 15 tháng 11 năm 1630, và được chôn tại đây. Vị trí ngôi mộ của ông không còn nữa sau khi quân đội Thụy Điển phá hủy khu nghĩa trang.[76] Chỉ còn lời thơ đề bia mộ do chính Kepler soạn tồn tại với thời gian:
- Mensus eram coelos, nunc terrae metior umbras
- Mens coelestis erat, corporis umbra iacet.
- Tôi đã đo những tầng trời, và giờ đây tôi đo chiếc bóng
- Tinh thần nằm lại góc trời, thể xác nghỉ nơi cội đất.[77]
Sự đón nhận thiên văn học Kepler
[sửa | sửa mã nguồn]Các định luật Kepler khi xuất hiện không có sự đón nhận nồng nhiệt. Một số nhân vật quan trọng đương thời như Galileo và René Descartes hoàn toàn phớt lờ tác phẩm Astronomia nova. Nhiều nhà thiên văn, bao gồm chính thầy dạy của Kepler, Michael Maestlin, phản đối việc Kepler đưa vật lý vào thiên văn học của ông. Một vài người có thái độ lưng chừng. Ismael Boulliau chấp nhận các quỹ đạo elip nhưng thay định luật về diện tích quỹ đạo của Kepler với chuyển động đều ứng với tiêu điểm trống (đối diện Mặt Trời) của elip, trong khi giám mục Seth Ward sử dụng một quỹ đạo elip với chuyển động xác định bằng một đẳng thước.[78][79][80]
Một vài nhà thiên văn đã kiểm tra lý thuyết của Kepler, và những sửa đổi khác nhau của nó, với các quan sát thiên văn. Hai lần đi qua Mặt Trời của Sao Kim và Sao Thủy cho phép kiểm tra tính phù hợp của lý thuyết, vì theo giả thuyết quỹ đạo tròn thông thường các hành tinh này sẽ không quan sát được trong điều kiện đó. Trong trường hợp Sao Thủy băng qua Mặt Trời năm 1631, Kepler hết sức không chắc chắn về các tham số cho Sao Thủy nên đã khuyên những người quan sát trông đợi sự kiện đó trong sai số một ngày so với dự đoán. Pierre Gassendi đã quan sát được hiện tượng vào đúng ngày dự đoán và do đó xác nhận những tiên đoán của Kepler.[81] Đây chính là lần đầu tiên người ta quan sát được hiện tượng Sao Thủy băng qua Mặt Trời. Tuy nhiên, nỗ lực của nhà thiên văn người Pháp này nhằm quan sát Sao Kim ngang qua Mặt Trời một tháng sau đó đã bất thành do sai sót trong bảng Rudolf. Gassendi không nhận ra rằng hiện tượng này không thể quan sát đối với phần lớn châu Âu, gồm cả Paris nơi ông sống.[82] Jeremiah Horrock, người quan sát hiện tượng này lặp lại vào năm 1639, đã sử dụng những quan sát của chính ông để hiệu chỉnh các thông số trong mô hình Kepler, tiên đoán hiện tượng Sao Kim vượt Mặt Trời, và sau đó thiết lập dụng cụ để quan sát nó. Thành công khiến ông trở thành một người bênh vực nhiệt thành cho mô hình Kepler.[83][84][85]
Cuốn Thiên văn học Copernicus giản lược của Kepler lưu hành rộng rãi trong giới thiên văn học khắp châu Âu đương thời, và chính là tác phẩm chính truyền tải rộng rãi những tư tưởng của Kepler sau khi ông mất. Nó từng là sách giáo khoa thiên văn sử dụng phổ biến nhất trong những năm 1630-1650, giúp cho nhiều người tin vào thiên văn học dựa trên quỹ đạo elip.[62] Tuy nhiên, ít người quan tâm áp dụng những ý tưởng về cơ sở vật lý của Kepler cho chuyển động thiên thể. Cuối thế kỷ 17, một số lý thuyết thiên văn học rút từ các công trình của Kepler-đáng chú ý là của Giovanni Alfonso Borelli và Robert Hooke-bắt đầu kết hợp lực hút (chứ không phải là loại chuyển động tựa tinh thần mà Kepler đề xuất) và quan niệm Descartes về quán tính. Tất cả hội tụ và kết tinh trong cuốn Những nguyên lý toán học của triết học tự nhiên (1687) của Isaac Newton, trong đó Newton rút được các định luật của Kepler về chuyển động hành tinh từ một lý thuyết lực về vạn vật hấp dẫn.[86]
Di sản và vinh danh
[sửa | sửa mã nguồn]
Bên cạnh vai trò của ông trong lịch sử phát triển của thiên văn học và triết học tự nhiên, Kepler cũng có một vị trí nổi bật trong triết học và lịch sử khoa học. Kepler với những định luật chuyển động hành tinh của mình là trung tâm của những tác phẩm đầu tiên về lịch sử thiên văn và toán học như Histoire des mathematiques (Lịch sử toán học, 1758) của Jean-Étienne Montucla và Histoire de l'astronomie moderne (Lịch sử thiên văn hiện đại, 1821) của Jean-Baptiste Delambre. Chúng cũng như các nghiên cứu khác viết dưới nhãn quan Thời kỳ Khai sáng thường xem xét các lập luận siêu hình và tôn giáo của Kepler với óc hoài nghi và sự phản đối, nhưng các triết gia tự nhiên thời sau đó thuộc chủ nghĩa lãng mạn (thế kỷ 19) coi chính những yếu tố này là trung tâm thành tựu của ông. William Whewell, trong cuốn sách gây ảnh hưởng History of the Inductive Sciences (Lịch sử Khoa học Quy nạp, 1837) xem Kepler như là nguyên mẫu của thiên tài khoa học quy nạp; và trong cuốn Philosophy of the Inductive Sciences (Triết học Khoa học Quy nạp, 1840), Whewell tiếp tục gọi Kepler là hiện thân của những dạng tiến bộ nhất trong phương pháp khoa học. Tương tự, Ernst Friedrich Apelt—người đầu tiên nghiên cứu rộng rãi các bản thảo Kepler, sau khi Ekaterina II của Nga mua chúng—xác định Kepler là chìa khóa của Cách mạng khoa học". Apelt, người xem toán học, tính nhạy cảm mĩ học, ý tưởng vật lý, và thần học của Kepler như một phần của một hệ thống tư tưởng thống nhất, tạo nên phân tích bao quát đầu tiên về cuộc đời và sự nghiệp Kepler.[87]
Các bản dịch hiện đại của một số trong những sách của Kepler vào cuối thế kỉ 19 và đầu thế kỉ 20, trong khi việc công bố các hệ thống các tác phẩm chọn lọc của ông bắt đầu từ năm 1937 (và tới đầu thế kỉ 21 đã gần như hoàn thành), trong khi tiểu sử Kepler của Max Caspar in năm 1948.[88] Tuy nhiên, công trình của Alexandre Koyré về Kepler mới là dấu mốc quan trọng tiếp theo, sau Apelt, trong quá trình diễn dịch vũ trụ học Kepler và ảnh hưởng của nó. Trong những năm 1930 và 1940, Koyré và một số những sử gia chuyên về khoa học khác, đã mô tả Cách mạng khoa học thời cận đại là sự kiện chủ chốt trong lịch sử khoa học. Koyré xếp lý thuyết của Kepler, hơn là công trình thực nghiệm của ông, vào tâm điểm của sự chuyển dịch tinh thần từ thế giới quan cổ đại sang hiện đại. Từ những năm 1960, khối lượng nghiên cứu về Kepler tăng mạnh, bao gồm những nghiên cứu về chiêm tinh và khí tượng học của ông, các phương pháp hình học, cũng như vai trò của quan điểm tôn giáo trong nghiên cứu của ông, các phương pháp văn học và hùng biện, giao tiếp của ông với những dòng chảy văn hóa và triết học rộng lớn hơn của thời đại đó, và thậm chí cả vai trò của ông như một sử gia khoa học[89]
Cuộc tranh cãi về vị trí của Kepler trong cuộc Cách mạng Khoa học cũng sản sinh ra hàng loạt cuộc luận bàn triết học lẫn đại chúng. Trong số chúng có tầm ảnh hưởng lớn phải kể đến The Sleepwalkers (Những kẻ mộng du, 1959) của Arthur Koestler, trong đó Kepler rõ ràng là người anh hùng (cả về đạo đức, thần học, lẫn trí tuệ) của cuộc cách mạng.[90] Các triết gia khoa học-như Charles Sanders Peirce, Norwood Russell Hanson, Stephen Toulmin, và Karl Popper-liên tục nhắc tới Kepler: các ví dụ về tính bất khả sánh, suy luận loại suy, tính khả kiểm, và nhiều khái niệm triết học khác đã được tìm thấy trong các tác phẩm của Kepler. Nhà vật lý Wolfgang Pauli thậm chí còn dùng tranh cãi quyền tác giả giữa Kepler với Robert Fludd để khám phá những ngụ ý của tâm lý học phân tích đối với nghiên cứu khoa học.[91] Một tiểu thuyết lịch sử có ít nhiều hư cấu được đánh giá cao của John Banville, Kepler (1981), khám phá nhiều đề tài được phát triển trong tường thuật phi tiểu thuyết của Koestler và triết học khoa học[92]. Chứa nhiều hư cấu hơn là một tác phẩm phi tiểu thuyết khác, Heavenly Intrigue (tạm dịch: Mưu mô Bầu trời, 2004), đề xuất rằng Kepler đã mưu sát Tycho Brahe để chiếm đoạt dữ liệu.[93] Kepler mang một hình ảnh đại chúng như là biểu tượng của tính hiện đại khoa học và một người đi trước thời đại mình; tác giả phổ biến khoa học Carl Sagan mô tả ông là "nhà vật lý thiên văn đầu tiên và nhà chiêm tinh khoa học cuối cùng".[94] Kepler cũng xuất hiện trong nhiều tác phẩm nghệ thuật khác, chẳng vở opera Die Harmonie der Welt và bản giao hưởng cùng tên của Paul Hindemith.[95]
Để vinh danh Kepler, bên cạnh những định luật và khái niệm toán học mang tên Kepler đã nhắc trong bài, rất nhiều địa danh, đường sá, sự kiện,... được đặt theo tên ông. Ở Áo, năm 2002 hình ông được đúc trong một đồng xu euro tưởng niệm, mà giới sưu tập gọi là đồng 10-euro bạc Johannes Kepler[96]. Ở New Zealand có dãy núi Kepler và con đường Kepler xuyên qua dãy núi là một địa điểm thu hút khách du lịch.[97] Tên ông cũng được đặt cho một số trường học như Cao đẳng Kepler (Seattle), Trường Ngữ pháp Johannes Kepler (Praha), Đại học Johannes Kepler Linz,... Đặc biệt, rất nhiều tên trong lĩnh vực thiên văn được đặt theo tên ông, bao gồm các hố va chạm trên Mặt Trăng, Sao Hỏa, tiểu hành tinh 1134 Kepler, hành tinh ngoài hệ Mặt Trời Kepler-22b ATV, Đài thiên văn không gian Kepler,...[98]
Kepler được kính nhớ cùng với Copernicus vào ngày 23 tháng 5 trong lịch phụng vụ của Giáo hội Giám nhiệm (Hoa Kỳ).[99]
Tác phẩm
[sửa | sửa mã nguồn]
- Mysterium cosmographicum (1596)
- De Fundamentis Astrologiae Certioribus (1601)
- Astronomiae Pars Optica (1604)
- De Stella nova in pede Serpentarii (1604)
- Astronomia nova (1609)

- De nive sexangula (1611)
- De vero Anno, quo aeternus Dei Filius humanam naturam in Utero benedictae Virginis Mariae assumpsit (1614)
- Eclogae Chronicae (1615)
- Nova stereometria doliorum vinariorum (1615)
- Epitome astronomiae Copernicanae (3 phần, 1618–1621)
- Harmonices Mundi (1619)
- Mysterium cosmographicum, tái bản (1621)
- Tabulae Rudolphinae (1627)
- Somnium (1634)
Xem thêm
[sửa | sửa mã nguồn]Chú thích
[sửa | sửa mã nguồn]- ^ Liscia, Daniel A. Di. “Johannes Kepler”. Trong Zalta, Edward N. (biên tập). Stanford Encyclopedia of Philosophy (bằng tiếng Anh).
- ^ Dudenredaktion; Kleiner, Stefan; Knöbl, Ralf (2015) [First published 1962]. Das Aussprachewörterbuch [The Pronunciation Dictionary] (bằng tiếng Đức) (ấn bản thứ 7). Berlin: Dudenverlag. tr. 487, 505. ISBN 978-3-411-04067-4.
- ^ Krech, Eva-Maria; Stock, Eberhard; Hirschfeld, Ursula; Anders, Lutz Christian (2009). Deutsches Aussprachewörterbuch [German Pronunciation Dictionary] (bằng tiếng Đức). Berlin: Walter de Gruyter. tr. 628, 646. ISBN 978-3-11-018202-6. Bản gốc lưu trữ ngày 3 tháng 10 năm 2020. Truy cập ngày 11 tháng 8 năm 2021.
- ^ Barker và Goldstein. "Theological Foundations of Kepler's Astronomy", tr. 112–13.
- ^ Kepler. New Astronomy, trang tựa, P. Donohue, tr. 26–7.
- ^ Kepler. New Astronomy, tr. 48.
- ^ Epitome of Copernican Astronomy trong Great Books of the Western World, tập 15, tr. 845.
- ^ Stephenson. Kepler's Physical Astronomy, tr. 1–2; Dear, Revolutionizing the Sciences, tr. 74–78.
- ^ Caspar. Kepler, tr. 29–36; Connor. Kepler's Witch, tr. 23–46.
- ^ a b Koestler. The Sleepwalkers, tr. 234 (theo gia phả gia đình Kepler).
- ^ Caspar. Kepler, tr. 36–38; Connor. Kepler's Witch, tr. 25–27.
- ^ Connor, James A. Kepler's Witch (2004), tr. 58.
- ^ a b Barker, Peter; Goldstein, Bernard R. "Theological Foundations of Kepler's Astronomy", Osiris, Phần 2, Tập 16, Science trong Theistic Contexts: Cognitive Dimensions (2001), tr. 96.
- ^ Westman, Robert S. "Kepler's Early Physico-Astrological Problematic," Journal for the History of Astronomy, 32 (2001): 227–36.
- ^ Caspar. Kepler, tr. 38–52; Connor. Kepler's Witch, tr. 49–69.
- ^ Caspar. Kepler, tr. 60–65; xem thêm: Barker và Goldstein, "Theological Foundations of Kepler's Astronomy."
- ^ Barker and Goldstein. "Theological Foundations of Kepler's Astronomy," pp. 99–103, 112–113.
- ^ Caspar. Kepler, pp. 65–71.
- ^ Field. Kepler's Geometrical Cosmology, Chapter IV, tr 73ff.
- ^ Dreyer, J.L.E. A History of Astronomy from Thales to Kepler, Dover Publications, 1953, tr. 331, 377–379.
- ^ Caspar, Kepler. tr. 71–75.
- ^ Connor. Kepler's Witch, tr. 89–100, 114–116; Caspar. Kepler, tr. 75–77
- ^ Caspar. Kepler, tr. 85–86.
- ^ Caspar, Kepler, tr. 86–89
- ^ Caspar, Kepler, tr. 89–100
- ^ “Về việc Kepler sử dụng dữ liệu Tycho, xem 'Two views of a system'”. Bản gốc lưu trữ ngày 16 tháng 1 năm 2014. Truy cập ngày 16 tháng 1 năm 2014.
- ^ Caspar, Kepler, tr. 100–08.
- ^ Caspar, Kepler, tr. 110.
- ^ Caspar, Kepler, tr. 108–11.
- ^ Mallia, Daniel (ngày 16 tháng 1 năm 2012). “Did Johannes Kepler murder Tycho Brahe?”. History News Network. Lưu trữ bản gốc ngày 21 tháng 1 năm 2012. Truy cập ngày 19 tháng 1 năm 2012.
- ^ Gannon, Megan (ngày 16 tháng 11 năm 2012). “Tycho Brahe Died from Pee, Not Poison”. LiveScience. Lưu trữ bản gốc ngày 19 tháng 11 năm 2012. Truy cập ngày 17 tháng 11 năm 2012.
- ^ Caspar, Kepler, tr. 111–22.
- ^ Caspar, Kepler, tr. 149–53
- ^ Caspar, Kepler, tr. 146–148, 159–177
- ^ a b Finger, "Origins of Neuroscience," tr 74. Oxford University Press, 2001.
- ^ Morris Kline, Mathematical Thought from Ancient to Modern Times, tr. 299. Oxford University Press, 1972.
- ^ Caspar, Kepler, tr. 153–157
- ^ Caspar, Kepler, tr. 123–128
- ^ Về loại chuyển động, xem: Lindberg, "The Genesis of Kepler's Theory of Light," tr. 38–40
- ^ Peter Barker and Bernard R. Goldstein, "Distance and Velocity in Kepler's Astronomy", Annals of Science, 51 (1994): 59–73, tr. 60.
- ^ Koyré, The Astronomical Revolution, tr. 199–202
- ^ Caspar, Kepler, tr. 129–132
- ^ Caspar, Kepler, tr. 131–140; Koyré, The Astronomical Revolution, tr. 277–279
- ^ Caspar, Kepler, tr. 178–81
- ^ Caspar, Kepler, tr. 181–85. Tựa đề đầy đủ rất dài, có thể dịch ra là "Những can thiệp từ bên thứ ba, hay lời cảnh báo tới một vài triết gia, bác sĩ và nhà thần học, đặc biệt là ông Philip Feselius, rằng họ trong lời cáo buộc rẻ tiền về sự mê tín của những người quan sát tinh tú mắc một sai sót trầm trọng và do đó cư xử trái với nghề nghiệp của mình mà không biết".
- ^ “Kepler in Praha”. Lưu trữ bản gốc ngày 10 tháng 9 năm 2009. Truy cập ngày 9 tháng 1 năm 2014.
- ^ Caspar, Kepler, tr. 192–197
- ^ Koestler, The Sleepwalkers tr. 384
- ^ Caspar, Kepler, tr. 198–202
- ^ Carl Sagan. Carl Sagan on Johannes Kepler's persecution. Lưu trữ bản gốc ngày 14 tháng 12 năm 2013. Truy cập ngày 9 tháng 1 năm 2014.
- ^ Lear, Kepler's Dream, tr. 1–78
- ^ Schneer, "Kepler's New Year's Gift of a Snowflake," tr. 531–45
- ^ Kepler, Johannes (1966) [1611]. Hardie, Colin (biên tập). De nive sexangula [The Six-sided Snowflake]. Oxford: Clarendon Press. OCLC 974730.
- ^ Caspar, Kepler, tr. 202–204
- ^ Connor, Kepler's Witch, tr. 222–226; Caspar, Kepler, tr. 204–07
- ^ Caspar, Kepler, tr. 208–11
- ^ Caspar, Kepler, tr. 209–20, 227–240
- ^ Ferguson, Thomas S. (1989), “Who solved the secretary problem ?”, Statistical Science, 4 (3): 282–289, Bản gốc lưu trữ ngày 18 tháng 4 năm 2021, truy cập ngày 11 tháng 1 năm 2014
- ^ Trích từ Connor, Kepler's Witch, tr. 252, dịch từ một lá thư ngày 23 tháng 10 năm 1613 của Kepler cho một nhà quý tộc khuyết danh
- ^ Caspar, Kepler, tr. 220–223; Connor, Kepler's Witch, tr. 251–54.
- ^ Caspar, Kepler, tr. 239–240, 293–300
- ^ a b Gingerich, "Kepler, Johannes" từ Dictionary of Scientific Biography, tr. 302–04
- ^ Ít nhất từ năm 1622, Kepler đã nhận ra các mặt trăng của Sao Mộc tuân theo định luật thứ ba của ông. Chi tiết xem thêm tại Christian Frisch, ed., Joannis Kepleri Astronomi Opera Omnia, vol. 6 (Frankfurt-am-Main, (Germany): Heyder & Zimmer, 1866), tr 361 Lưu trữ 2021-04-15 tại Wayback Machine
- ^ Wolf, A History of Science, Technology and Philosophy, tr. 140–41; Pannekoek, A History of Astronomy, tr. 252
- ^ Caspar, Kepler, tr. 239, 300–01, 307–08
- ^ Caspar, Kepler, tr. 240–264; Connor, Kepler's Witch, các chương I, XI-XIII; Lear, Kepler's Dream, tr. 21–39
- ^ trích từ Caspar, Kepler, tr. 265–266, dịch từ Harmonices Mundi
- ^ Theo Science-fiction romantique Lưu trữ 2015-05-08 tại Wayback Machine, mở đầu phim Mars et Avril của Martin Villeneuve dựng theo mô hình này của Kepler
- ^ Caspar, Kepler, tr. 264–66, 290–93
- ^ Caspar, Kepler, tr. 266–90
- ^ Arthur I. Miller (ngày 24 tháng 3 năm 2009). Deciphering the cosmic number: the strange friendship of Wolfgang Pauli and Carl Jung. W. W. Norton & Company. tr. 80. ISBN 978-0-393-06532-9. Bản gốc lưu trữ ngày 4 tháng 5 năm 2015. Truy cập ngày 7 tháng 3 năm 2011.
- ^ Westfall, Never at Rest, tr. 143, 152, 402–03; Toulmin và Goodfield, The Fabric of the Heavens, tr 248; De Gandt, 'Force and Geometry in Newton's Principia', chương 2; Wolf, History of Science, Technology and Philosophy, tr. 150; Westfall, The Construction of Modern Science, chương 7, 8
- ^ Koyré, The Astronomical Revolution, tr. 502
- ^ Walter William Bryant, Kepler Lưu trữ 2013-04-30 tại Wayback Machine The Macmillan Company (1920) tr.35
- ^ Caspar, Kepler, tr. 308–328
- ^ Caspar, Kepler, tr. 332–351, 355–61
- ^ Koestler, The Sleepwalkers, tr. 427.
- ^ Chi tiết về sự đón nhận thiên văn học Kepler, xem Wilbur Applebaum, "Keplerian Astronomy after Kepler: Researches and Problems," Lưu trữ 2015-12-28 tại Wayback Machine History of Science, 34(1996): 451–504.
- ^ Koyré, The Astronomical Revolution, tr. 362–364
- ^ North, History of Astronomy and Cosmology, tr. 355–60
- ^ Albert van Helden, "The Importance of the Transit of Mercury of 1631," Lưu trữ 2017-07-12 tại Wayback Machine Journal for the History of Astronomy, 7 (1976): 1–10.
- ^ HM Nautical Almanac Office (ngày 10 tháng 6 năm 2004). “1631 Transit of Venus”. Bản gốc lưu trữ ngày 1 tháng 10 năm 2006. Truy cập ngày 28 tháng 8 năm 2006.
- ^ Allan Chapman, "Jeremiah Horrocks, the transit of Venus, and the 'New Astronomy' in early 17th-century England," Lưu trữ 2017-07-12 tại Wayback Machine Quarterly Journal of the Royal Astronomical Society, 31 (1990): 333–357.
- ^ North, History of Astronomy and Cosmology, tr. 348–349
- ^ Wilbur Applebaum và Robert Hatch, "Boulliau, Mercator, and Horrock's Venus in sole visa: Three Unpublished Letters," Lưu trữ 2017-07-12 tại Wayback Machine Journal for the History of Astronomy, 14(1983): 166–179
- ^ Kuhn, The Copernican Revolution, tr. 238, 246–252
- ^ Jardine, "Koyré's Kepler/Kepler's Koyré," tr. 363–367
- ^ Gingerich, introduction to Caspar's Kepler, tr. 3–4
- ^ Jardine, "Koyré's Kepler/Kepler's Koyré," tr. 367–372; Shapin, The Scientific Revolution, tr. 1–2
- ^ Stephen Toulmin, Phê bình The Sleepwalkers trong The Journal of Philosophy, tập 59, 18 (1962), tr. 500–503
- ^ Pauli, "The Influence of Archetypical Ideas"
- ^ William Donahue, "A Novelist's Kepler," Journal for the History of Astronomy, Vol. 13 (1982), pp. 135–136; "Dancing the grave dance: Science, art and religion in John Banville's Kepler," English Studies, Vol. 86, no. 5 (October 2005), tr. 424–438
- ^ Marcelo Gleiser, "Kepler in the Dock", review of Gilder and Gilder's Heavenly Intrigue, Journal for the History of Astronomy, Vol. 35, pt. 4 (2004), pp. 487–489
- ^ Trích từ tập 3 của series Cosmos: A Personal Voyage Lưu trữ 2013-11-10 tại Wayback Machine của Carl Sagan.
- ^ “Die Harmonie der Welt”. Schott Music. Lưu trữ bản gốc ngày 1 tháng 2 năm 2013. Truy cập ngày 5 tháng 11 năm 2012.
- ^ “Eggenberg Palace coin”. Austrian Mint. Bản gốc lưu trữ ngày 31 tháng 5 năm 2011. Truy cập ngày 9 tháng 9 năm 2009.
- ^ “Kepler Track” (PDF). New Zealand Department of Conservation. 2007. Lưu trữ (PDF) bản gốc ngày 3 tháng 10 năm 2012. Truy cập ngày 18 tháng 5 năm 2007.
- ^ DeVore, Edna (ngày 9 tháng 6 năm 2008). “Closing in on Extrasolar Earths”. SPACE.com. Lưu trữ bản gốc ngày 16 tháng 7 năm 2009. Truy cập ngày 14 tháng 3 năm 2009.
- ^ “Calendar of the Church Year according to the Episcopal Church”. Lưu trữ bản gốc ngày 23 tháng 8 năm 2000. Truy cập ngày 16 tháng 1 năm 2014.
Tiểu sử đầy đủ nhất về Kepler là của Max Caspar. Mặc dù gần đây có những tiểu sử mới hơn nhưng hầu hết đều dựa trên công trình của Caspar mà ít có thêm nghiên cứu riêng mới nào, do đó nguồn tham khảo trong bài này lấy từ đây. Phần nhiều thông tin được trích từ Caspar cũng có thể tìm thấy trong các sách của Arthur Koestler, Kitty Ferguson, và James A. Connor. "The Eye of Heaven" của Owen Gingerich dựa trên công trình Caspar, đặt vào một bối cảnh rộng lớn hơn của thiên văn học cận đại. Hầu hết các nghiên cứu về sau tập trung vào những yếu tố cụ thể trong cuộc đời và sự nghiệp của Kepler. Trong khi các quan điểm toán học, vũ trụ học, triết học và lịch sử của Kepler được phân tích rất nhiều trong các bài báo và sách, các công trình chiêm tinh và mối liên hệ với thiên văn học của ông tương đối ít được nghiên cứu.
Thư mục
[sửa | sửa mã nguồn]- Andersen, Hanne; Peter Barker; và Xiang Chen. The Cognitive Structure of Scientific Revolutions, chapter 6: "The Copernican Revolution." New York: Cambridge University Press, 2006. ISBN 0-521-85575-6
- Armitage, Angus. John Kepler, Faber, 1966.
- Banville, John. Kepler, Martin, Secker and Warburg, London, 1981 (fictionalised biography)
- Barker, Peter và Bernard R. Goldstein: "Theological Foundations of Kepler's Astronomy". Osiris, Volume 16. Science in Theistic Contexts. University of Chicago Press, 2001, pp. 88–113
- Caspar, Max. Kepler; dịch và biên tập bởi C. Doris Hellman; với dẫn nhập và tham khảo từ Owen Gingerich; trích dẫn thư mục bởi Owen Gingerich và Alain Segonds. New York: Dover, 1993. ISBN 0-486-67605-6
- Connor, James A. Kepler's Witch: An Astronomer's Discovery of Cosmic Order Amid Religious War, Political Intrigue, and the Heresy Trial of His Mother. HarperSanFrancisco, 2004. ISBN 0-06-052255-0
- De Gandt, Francois. Force and Geometry in Newton's Principia, Translated by Curtis Wilson, Princeton University Press 1995. ISBN 0-691-03367-6
- Dreyer, J. L. E. A History of Astronomy from Thales to Kepler. Dover Publications Inc, 1967. ISBN 0-486-60079-3
- Ferguson, Kitty. The nobleman and his housedog: Tycho Brahe and Johannes Kepler: the strange partnership that revolutionized science. London: Review, 2002. ISBN 0-7472-7022-8 – published in the US as: Tycho & Kepler: the unlikely partnership that forever changed our understanding of the heavens. New York: Walker, 2002. ISBN 0-8027-1390-4
- Field, J. V.. Kepler's geometrical cosmology. Chicago University Press, 1988. ISBN 0-226-24823-2
- Gilder, Joshua và Anne-Lee Gilder: Heavenly Intrigue: Johannes Kepler, Tycho Brahe, and the Murder Behind One of History's Greatest Scientific Discoveries, Doubleday (ngày 18 tháng 5 năm 2004). ISBN 0-385-50844-1
- Gingerich, Owen. The Eye of Heaven: Ptolemy, Copernicus, Kepler. American Institute of Physics, 1993. ISBN 0-88318-863-5 (Masters of modern physics; v. 7)
- Gingerich, Owen: "Kepler, Johannes" in Dictionary of Scientific Biography, Volume VII. Charles Coulston Gillispie, editor. New York: Charles Scribner's Sons, 1973
- Greenbaum và Boockmann: "Kepler's Astrology", Culture and Cosmos Vol. 14. Special Double Issue, 2012.
- Jardine, Nick: "Koyré's Kepler/Kepler's Koyré," History of Science, Vol. 38 (2000), pp. 363–376
- Kepler, Johannes. Johannes Kepler New Astronomy dịch W. Donahue, tựa bởi O. Gingerich, Cambridge University Press 1993. ISBN 0-521-30131-9
- Kepler, Johannes và Christian Frisch. Joannis Kepleri Astronomi Opera Omnia (John Kepler, Astronomer; Complete Works), 8 vols.(1858–1871). vol. 1, 1858 Lưu trữ 2021-04-15 tại Wayback Machine, vol. 2, 1859 Lưu trữ 2021-04-15 tại Wayback Machine, vol. 3, 1860 Lưu trữ 2021-04-15 tại Wayback Machine, vol. 6, 1866 Lưu trữ 2021-04-15 tại Wayback Machine, vol. 7, 1868 Lưu trữ 2011-07-21 tại Wayback Machine, Frankfurt am Main and Erlangen, Heyder & Zimmer, – Google Books
- Kepler, Johannes, et al. Great Books of the Western World. Volume 16: Ptolemy, Copernicus, Kepler, Chicago: Encyclopædia Britannica, Inc., 1952. (
- Koestler, Arthur. The Sleepwalkers: A History of Man's Changing Vision of the Universe. (1959). ISBN 0-14-019246-8
- Koyré, Alexandre: Galilean Studies Harvester Press 1977. ISBN 0-85527-354-2
- Koyré, Alexandre: The Astronomical Revolution: Copernicus-Kepler-Borelli Ithaca, NY: Cornell University Press, 1973. ISBN 0-8014-0504-1; Methuen, 1973. ISBN 0-416-76980-2; Hermann, 1973. ISBN 2-7056-5648-0
- Kuhn, Thomas S. The Copernican Revolution: Planetary Astronomy in the Development of Western Thought. Cambridge, MA: Harvard University Press, 1957. ISBN 0-674-17103-9
- Lindberg, David C.: "The Genesis of Kepler's Theory of Light: Light Metaphysics from Plotinus to Kepler." Osiris, N.S. 2. University of Chicago Press, 1986, pp. 5–42.
- Lear, John. Kepler's Dream. Berkeley: University of California Press, 1965
- M.T.K Al-Tamimi: Great collapse Kepler's first law, Natural Science 2 (2010), ISBN 2150 – 4091
- North, John. The Fontana History of Astronomy and Cosmology, Fontana Press, 1994. ISBN 0-00-686177-6
- Pannekoek, Anton: A History of Astronomy, Dover Publications Inc 1989. ISBN 0-486-65994-1
- Pauli, Wolfgang. Wolfgang Pauli — Writings on physics and philosophy, dịch bởi Robert Schlapp và biên tập bởi P. Enz và Karl von Meyenn (Springer Verlag, Berlin, 1994). Xem 21, The influence of archetypical ideas on the scientific theories of Kepler, liên quan vụ việc Johannes Kepler và Robert Fludd (1574–1637). ISBN 3-540-56859-X
- Schneer, Cecil: "Kepler's New Year's Gift of a Snowflake." Isis, Volume 51, No. 4. University of Chicago Press, 1960, pp. 531–545.
- Shapin, Steven. The Scientific Revolution. Chicago: University of Chicago Press, 1996. ISBN 0-226-75020-5
- Stephenson, Bruce. Kepler's physical astronomy. New York: Springer, 1987. ISBN 0-387-96541-6 (Studies in the history of mathematics and physical sciences; 13); reprinted Princeton:Princeton Univ. Pr., 1994. ISBN 0-691-03652-7
- Stephenson, Bruce. The Music of the Heavens: Kepler's Harmonic Astronomy, Princeton University Press, 1994. ISBN 0-691-03439-7
- Toulmin, Stephen và June Goodfield. The Fabric of the Heavens: The Development of Astronomy and Dynamics. Pelican, 1963.
- Voelkel, James R. The Composition of Kepler's Astronomia nova, Princeton University Press, 2001. ISBN 0-691-00738-1
- Westfall, Richard S.. The Construction of Modern Science: Mechanism and Mechanics. John Wiley and Sons, 1971. ISBN 0-471-93531-X; reprinted Cambridge University Press, 1978. ISBN 0-521-29295-6
- Westfall, Richard S. Never at Rest: A Biography of Isaac Newton. Cambridge University Press, 1981. ISBN 0-521-23143-4
- Wolf, A. A History of Science, Technology and Philosophy in the 16th and 17th centuries. George Allen & Unwin, 1950.
Liên kết ngoài
[sửa | sửa mã nguồn]| Tập tin phương tiện từ Commons | |
| Danh ngôn từ Wikiquote | |
| Văn kiện từ Wikisource | |
| Tủ sách giáo khoa từ Wikibooks | |
- Johannes Kepler (German astronomer) tại Encyclopædia Britannica (tiếng Anh)
- KÊPLƠ I. tại Từ điển bách khoa Việt Nam
- Kommission zur Herausgabe der Werke von Johannes Kepler Lưu trữ 2016-12-02 tại Wayback Machine
- JohannesKepler.Info Trang web về Kepler, ra đời năm 2009
- Harmonices mundi Vũ trụ Hài hòa bản đầy đủ; Đại học Carnegie-Mellon
- Mục nhập "Johannes Kepler" bởi Daniel A. Di Liscia trong Bách khoa Toàn thư Triết học Stanford
- De Stella Nova in Pede Serpentarii Lưu trữ 2017-12-20 tại Wayback Machine bản đầy đủ tại Thư viên Linda Hall
- Walter W. Bryant. Kepler tại Dự án Gutenberg
- Ấn bản điện tử của tuyển tập sách hiếm tại Viện Thiên văn học Vienna
- Johannes Kepler trên DMOZ
- Audio – Cain/Gay (2010) Astronomy Cast Johannes Kepler and His Laws of Planetary Motion
- Christianson, Gale E., Kepler's Somnium: Science Fiction and the Renaissance Scientist
- Kollerstrom, Nicholas, Kepler's Belief in Astrology
- References for Johannes Kepler
- Plant, David, Kepler and the "Music of the Spheres"
- Kepler, Napier, and the Third Law trên MathPages
- Calderón Urreiztieta, Carlos. Harmonice Mundi
- Johannes Kepler, vở kịch năm 2010 về ông bởi Robert Lalonde
- O'Connor, John J.; Robertson, Edmund F., “Johannes Kepler”, Bộ lưu trữ lịch sử toán học MacTutor, Đại học St. Andrews
- Online Galleries, History of Science Collections, University of Oklahoma Libraries Lưu trữ 2021-04-26 tại Wayback Machine Ảnh độ phân giải cao về Kepler định dạng.jpg và.tiff.
 GIẢM
20%
GIẢM
20%
 GIẢM
32%
GIẢM
32%
 GIẢM
19%
GIẢM
19%
 GIẢM
38%
GIẢM
38%
 GIẢM
48%
GIẢM
48%
 GIẢM
15%
GIẢM
15%




