Teoria de la computació

La teoria de la computació és una ciència, en particular una branca de la matemàtica i de la computació que tracta de quins problemes es poden resoldre en un model de càlcul, mitjançant un algorisme, de quina manera es poden resoldre de manera eficient o en quin grau (per exemple, les solucions aproximades enfront de les precises). Dit d'una altra manera, dés la branca que estudia problemes de decidibilitat.^[1] El camp es divideix en tres grans branques: teoria dels autòmats i llenguatges formals, teoria de la computabilitat i teoria de la complexitat computacional, que es relacionen amb la pregunta: "Quines són les capacitats i limitacions fonamentals dels ordinadors?".^[2]

Per tal de dur a terme un estudi rigorós de la computació, els informàtics treballen amb una abstracció matemàtica dels ordinadors anomenada model de computació. Hi ha diversos models en ús, però el més freqüentment examinat és la màquina de Turing.^[3] perquè és senzilla de formular, es pot analitzar i utilitzar per demostrar resultats i perquè representa el que molts consideren el model de càlcul "raonable" més potent possible.^[4] Podria semblar que la capacitat de memòria potencialment infinita és un atribut irrealitzable, però qualsevol problema resolt per una màquina de Turing sempre requerirà només una quantitat finita de memòria.^[5]

Història

Vegeu també: Entscheidungsproblem i Tesi de Church-Turing

La teoria de la computació comença pròpiament a principis del segle xx, poc abans que les computadores electròniques fossin inventades. En aquesta època diversos matemàtics es preguntaven si existia un mètode universal per resoldre tots els problemes matemàtics. Per a això havien de desenvolupar la noció precisa de mètode per resoldre problemes, és a dir, la definició formal d'algorisme.

Des d'èpoques antigues, els còmputs han existit i s'han efectuat de manera mental o assistida per rudiments com comptes, llapis i paper, o taules. Els antecedents de la computació mecànica, poden traçar fins a èpoques antigues, amb el desenvolupament d'artefactes per assistir el procés dels càlculs matemàtics mentals, per exemple el àbac, el regle de càlcul o el quipu. Encara que potser és més propícia com a exemple precursor, la cèlebre calculadora grega d'Anticitera, utilitzada segons els experts per assistir en càlculs astronòmics, i considerada per molts com la primera ordinador.^[6] Un altre exemple precursor són les màquines sumador de Blaise Pascal. Aparells que demostren una notable perícia dels seus creadors en el coneixement sobre la forma d'elaborar els càlculs desitjats, al grau de poder representar en la forma de mecanismes més o menys elaborats.

Alguns d'aquests models formals van ser proposats per precursors com Alonzo Church (càlcul lambda), Kurt Gödel (funcions recursives) i Alan Turing (màquina de Turing).^[7] Aquests models són equivalents en el sentit que poden simular els mateixos algorismes, encara que ho facin de maneres diferents. Entre els models de còmput més recents hi ha els llenguatges de programació, que també han resultat ser equivalents als models anteriors, això és una forta evidència de la conjectura de Church-Turing, que tot algorisme hagut i per haver es pot simular en una màquina de Turing, o equivalent, usant funcions recursives. El 2007 Nachum Dershowitz i Yuri Gurevich van publicar una demostració d'aquesta conjectura basant-se en certa axiomatització d'algorismes.^[8]

Un dels primers resultats d'aquesta teoria va ser l'existència de problemes impossibles de resoldre algorítmicament, i el problema de la parada el més famós d'ells. Per a aquests problemes no existeix ni existirà cap algorisme que els pugui resoldre, no important la quantitat de temps o memòria es disposi en un ordinador. Així mateix, amb l'arribada de les computadores modernes es va constatar que alguns problemes resolubles en teoria eren impossibles en la pràctica, ja que aquestes solucions necessitaven quantitats irrealistes de temps o memòria per poder-se trobar.

Models de computació

En teoria de la computació, un model de càlcul és un model que descriu com es calcula una sortida d'una funció matemàtica donant una entrada. Un model descriu com s'organitzen les unitats de càlculs, memòries i comunicacions.^[9] La complexitat computacional d'un algorisme es pot mesurar donat un model de càlcul. L'ús d'un model permet estudiar el rendiment d'algoritmes independentment de les variacions específiques per a implementacions particulars i tecnologia específica.

El programari ha utilitzant massivament el model de computació per algorismes, però en els darrers anys, l'aprenentatge automàtic i el model de xarxa neuronal artificial han assolit notorietat i èxit, i computació quàntica comença a mostrar avanços significatius,^[10] i es desenvolupa la computació basada en ADN.^[11]

Branques

La teoria de la computació té diverses branques pròpies, entre elles:

• La Teoria dels llenguatges i gramàtiques formals, que és l'estudi i processament de llenguatges artificials, a través de la utilització de models simplificats de còmput, com són les autòmats finits i els autòmats amb pila.
• La complexitat, o l'estudi de la quantitat de temps i d'espai en memòria que pren l'execució d'un còmput donat.
• La Teoria de la computabilitat, o l'estudi i determinació de la classe de problemes que poden ser resolts en una màquina de Turing.

Teoria d'autòmats

Article principal: Teoria d'autòmats

Aquesta teoria proveeix models matemàtics que formalitzen el concepte d'ordinador o algorisme de manera prou simplificada i general perquè es puguin analitzar les seves capacitats i limitacions.^[12] Alguns d'aquests models tenen un paper central en diverses aplicacions de les ciències de la computació, incloent processament de text, compilador és, disseny de maquinari i intel·ligència artificial.

Els tres principals models són els autòmats finits, autòmats amb pila i màquines de Turing, cadascun amb les seves variants deterministes i no deterministes. Els autòmats finits són bons models d'ordinadors que tenen una quantitat limitada de memòria, els autòmats amb pila modelen els que tenen gran quantitat de memòria però que només poden manipular a manera d'pila (l'última dada emmagatzemat és el següent llegit), i les màquines de Turing modelen les computadores que tenen una gran quantitat de memòria emmagatzemada en una cinta. Aquests autòmats estan estretament relacionats amb la teoria de llenguatges formals, cada autòmat és equivalent a una gramàtica formal, el que permet reinterpretar la jerarquia de Chomsky en termes d'autòmats.

Existeixen molts altres tipus d'autòmats com les màquines d'accés aleatori, autòmats cel·lulars, àbacs i les màquines d'estat abstracte, però en tots els casos s'ha mostrat que aquests models no són més generals que la màquina de Turing, ja que la màquina de Turing té la capacitat de simular cada un d'aquests autòmats. Això dona lloc a que es pensi en la màquina de Turing com el model universal d'ordinador.

Gramàtica	Idiomes	Autòmat	Regles de producció (restriccions)
Tipus-0	Enumerable recursivament	Màquina de Turing	${\displaystyle \alpha \rightarrow \beta }$ (sense restriccions)
Tipus-1	Sensible al context	Màquina de Turing no determinista delimitada linealment	${\displaystyle \alpha A\beta \rightarrow \alpha \gamma \beta }$
Tipus-2	Sense context	Autòmat pushdown no determinista	${\displaystyle A\rightarrow \gamma }$
Tipus-3	Regular	Autòmat d'estat finit	${\displaystyle A\rightarrow a}$ </br> i </br> ${\displaystyle A\rightarrow aB}$

Teoria del llenguatge formal

Article principal: Llenguatge formal

Estableix inclusions descrites per la jerarquia de Chomsky

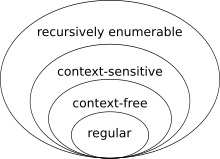
La teoria del llenguatge és una branca de les matemàtiques que s'encarrega de descriure les llengües com un conjunt d'operacions sobre un alfabet. Està molt lligat a la teoria dels autòmats, ja que els autòmats s'utilitzen per generar i reconèixer llenguatges formals. Hi ha diverses classes de llenguatges formals, cadascuna permet una especificació de llenguatge més complexa que l'anterior, és a dir jerarquia de Chomsky,^[13] i cadascuna corresponent a una classe d'autòmats que la reconeix. Com que els autòmats s'utilitzen com a models de càlcul, els llenguatges formals són el mode d'especificació preferit per a qualsevol problema que s'hagi de calcular.

Teoria de la computabilitat

Article principal: Teoria de la computabilitat

Aquesta teoria explora els límits de la possibilitat de solucionar problemes mitjançant algorismes. Gran part de les ciències computacionals estan dedicades a resoldre problemes de forma algorítmica, de manera que el descobriment de problemes impossibles és una gran sorpresa. La teoria de la computabilitat és útil per no tractar de resoldre algorítmicament aquests problemes, estalviant així temps i esforç.

Els problemes es classifiquen en aquesta teoria d'acord al seu grau d'impossibilitat :

• Els computables són aquells per als quals sí que existeix un algorisme que sempre els resol quan hi ha una solució ia més és capes de distingir els casos que no en tenen. També se'ls coneix com a decidibles , resolubles o recursius .
• Els semicomputables són aquells per als quals hi ha un algorisme que és capaç trobar una solució si és que existeix, però cap algorisme que determini quan la solució no existeix (en aquest cas l'algorisme per trobar la solució entraria a un bucle infinit). L'exemple clàssic per excel·lència és el problema de la parada. A aquests problemes també se'ls coneix com a listables , recursivament enumerables o recognoscibles , perquè si s'enlistan tots els casos possibles del problema, és possible reconèixer a aquells que sí que tenen solució.
• Els incomputabilitat són aquells per als quals no hi ha cap algorisme que els pugui resoldre, no important que tinguin o no solució. L'exemple clàssic per excel·lència és el problema de la implicació lògica, que consisteix a determinar quan una proposició lògica és un teorema; per aquest problema no hi ha cap algorisme que en tots els casos pugui distingir si una proposició o la seva negació és un teorema.

Hi ha una versió més general d'aquesta classificació, on els problemes incomputabilitat se subdivideixen al seu torn en problemes més difícils que altres. L'eina principal per aconseguir aquestes classificacions és el concepte de reducibilitat : Un problema ${\displaystyle A}$ es redueix al problema ${\displaystyle B}$ si sota la suposició que se sap resoldre el problema ${\displaystyle B}$ és possible resoldre el problema ${\displaystyle A}$, això es denota per ${\displaystyle A\leq _{t}B}$, i informalment vol dir que el problema ${\displaystyle A}$ no és més difícil de resoldre que el problema ${\displaystyle B}$. Per exemple, sota la suposició que una persona sap sumar, és molt fàcil ensenyar a multiplicar fent sumes repetides, de manera de multiplicar es redueix a sumar.

Teoria de la complexitat computacional

Representació de la relació entre classes de complexitat

Article principal: Complexitat computacional

Tot i que un problema sigui computable, potser no sigui possible resoldre en la pràctica si es requereix molta memòria o temps d'execució. La teoria de la complexitat computacional estudia les necessitats de memòria, temps i altres recursos computacionals per resoldre problemes, d'aquesta manera és possible explicar perquè uns problemes són més difícils de resoldre que altres. Un dels majors èxits d'aquesta branca és un la classificació de problemes, anàleg a la taula periòdica, d'acord amb la seva dificultat, en aquesta classificació els problemes se separen per classes de complexitat.

Aquesta teoria té aplicació en gairebé totes les àrees de coneixement on es vulgui resoldre un problema computacionalment, perquè els investigadors no només volen utilitzar un mètode per resoldre un problema, sinó utilitzar el més ràpid. La teoria de la complexitat computacional també té aplicacions en àrees com la criptografia, on s'espera que desxifrar un codi secret sigui un problema molt difícil a menys que es tingui la contrasenya, en aquest cas el problema es torna fàcil.

Altres subbranques

• Models de còmput Estudia abstraccions de fer un còmput. Aquí s'inclouen els clàssics models de la teoria d'autòmats més d'altres models com funcions recursives, càlcul lambda i fins i tot llenguatges de programació.
• Teoria algorísmica de la informació Centra la seva atenció en la complexitat per descriure algorismes una seqüència de dades (cadena); aquí la complexitat està mesura per la longitud de la seva descripció més petita .
• Especificació i verificació formal Busca metodologies per garantir que un problema estigui correctament modelatge i sistemes formals per a validar la correcció de la solució algorísmica.
• La Teoria de l'aprenentatge computacional cerca algorismes que facin que els ordinadors modifiquin els seus comportaments de manera autònoma amb base en dades empíriques, i concretament en exemples i contraexemples. A aquest tipus d'aprenentatge se l'anomena aprenentatge supervisat. De forma anàloga a la teoria de la complexitat computacional, en aquesta teoria les funcions es classifiquen pel seu grau de dificultat de ser apreses.
• Teoria de tipus Cerca la classificació d'enunciats d'acord amb els tipus de valors que calculen utilitzant eines de teoria de llenguatges formals.

Referències

1. «teoria de la computació». Gran Enciclopèdia Catalana. [Consulta: 15 agost 2022].
2. Sipser, 2013, p. 1.
3. Hodges, Andrew. Alan Turing: The Enigma (en anglès). The Centenary. Princeton University Press, 2012. ISBN 978-0-691-15564-7. 
4. Rabin, Michael O. (June 2012). Turing, Church, Gödel, Computability, Complexity and Randomization: A Personal View. 
5. Donald Monk. Mathematical Logic (en anglès). Springer-Verlag, 1976. ISBN 9780387901701. 
6. «Discovering How Greeks Computed in 100 B.C.». NY Times, 31-07-2008.
7. Pérez Jiménez, Mario de J.; Sancho Caparrini, Fernando. Máquinas moleculares basadas en ADN (en castellà). Universidad de Sevilla, 2003, p. 1. ISBN 8447207773. 
8. Nachum Dershowitz & Yuri Gurevich. A natural axiomatization of computability and proof of Church's Thesis. 14, 2008 (Bulletin of Symbolic Logic). 
9. «Models of Computation» (en anglès). [Consulta: 15 octubre 2021].
10. Antoniucci, Javier. «¿Cuáles son los nuevos modelos de computación?» (en castellà). Computing, 08-05-2020. [Consulta: 15 octubre 2021].
11. Chen, Yuan-Jyue; Dalchau, Neil; Srinivas, Niranjan; Phillips, Andrew; Cardelli, Luca «Programmable chemical controllers made from DNA». Nature nanotechnology, 8, 10, 10-2013, pàg. 755–762. DOI: 10.1038/nnano.2013.189. ISSN: 1748-3387. PMC: 4150546. PMID: 24077029.
12. «Basics of Automata Theory» (en anglès). Stanford Computer Science. [Consulta: 15 octubre 2021].
13. Chomsky hierarchy Information Theory, IRE Transactions on, 2, 3, 1956, pàg. 113–124. DOI: 10.1109/TIT.1956.1056813.

Bibliografia

• Michael Sipser. Introduction to the Theory of Computation 3rd (en anglès). Cengage Learning, 2013, p. 1. ISBN 978-1-133-18779-0. «central areas of the theory of computation: automata, computability, and complexity»