Kombinationston

Kombinationstöne können bei gleichzeitigem Erklingen zweier unterschiedlicher Töne entstehen, indem aus den beiden Grundfrequenzen (bzw. ihren Vielfachen) Differenzen oder Summen gebildet werden.

Kombinationstöne wurden gelegentlich Gegenstand der Musiktheorie, z. B. in Hindemiths Unterweisung im Tonsatz.

Entdeckung

Kombinationstöne, seinerzeit als Differenztöne bezeichnet, wurden 1714 von Giuseppe Tartini entdeckt^[1], 1744 in der «Anweisung zur Stimmung und Temperatur» von Georg Andreas Sorge beschrieben^[2] und 1754 von Giuseppe Tartini eingehender untersucht, später von Thomas Young, Johann August Wilhelm Röber und Hermann von Helmholtz. Letzterer hat mit Hilfe der Theorie auch einen zum Differenzton analogen höheren Ton entdeckt, dessen Schwingungszahl der Summe der Schwingungszahlen der erregenden Töne entspricht (Summationston).

Differenztöne

Jene Kombinationstöne, welche die mathematische Differenz zweier Töne darstellen, werden Differenztöne oder auch Tartini-Töne genannt, nach dem italienischen Geiger Giuseppe Tartini, der sie bei laut gespielten Doppelgriffen auf seiner Geige vernahm. Töne, welche die mathematische Summe zweier Frequenzen darstellen, werden als Summationstöne bezeichnet.

Der bekannteste und am leichtesten hörbare Differenzton ist der „quadratische“ Differenzton. Seine Frequenz $f_{D}$ entspricht der Schwebungsfrequenz, also der Differenz der Grundfrequenzen der beiden Ausgangstöne:

f_{D}=f_{2}-f_{1}

mit

f₂: Frequenz des höheren Tons
f₁: Frequenz des tieferen Tons.

Beispiel:

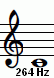
	Reine Sinustöne.		Bei kräftiger Lautstärke kann man diesen Kombinationston hören.

Summationstöne

Diese Töne stellen die Summe zweier Frequenzen dar und sind in der Regel deutlich seltener und schwerer wahrzunehmen. Sie sind manchmal, wie auch die Differenztöne, für die Entstehung als dissonant empfundener Töne bei Übersteuerung von Lautsprechern verantwortlich. Auch hier gilt, analog zum Differenzton:

f_{S}=f_{2}+f_{1}

mit

f₂: Frequenz des höheren Tons
f₁: Frequenz des tieferen Tons.

Geschulte Musiker hören weitere Differenzen und Summen der Vielfachen der Ausgangsfrequenzen als Kombinationstöne.

Im Orgelbau wird ein akustisches Phänomen fälschlicherweise Differenzton genannt. Eigentlich handelt es sich hier um Residualtöne; die keine Akustische Täuschung sind.

Im Ohr gebildet

Werden einem Beobachter zwei Primärtöne der Frequenzen f₁ < f₂ dargeboten, so entstehen im Ohr vor allem der quadratische Differenzton f₂ − f₁ und der kubische Differenzton 2 × f₁ − f₂. Unter geeigneten Bedingungen sind jedoch auch Differenztöne höherer Ordnung wahrnehmbar.

Im Ohr gebildete quadratische Differenztöne verhalten sich wie reguläre Verzerrungen, d. h. mit steigendem Schallpegel der Primärtöne steigt auch der Pegel des quadratischen Differenztons an.^[3]

Im Ohr gebildete kubische Differenztöne weisen nach Eberhard Zwicker jedoch einen „ungewöhnlichen Amplitudengang“ auf. Mit steigendem Pegel des höheren Primärtons wächst der Pegel des kubischen Differenztons zunächst an, wie dieses bei regulären Verzerrungen zu erwarten ist. Übersteigt der Pegel des höheren Primärtons jedoch den Pegel des niedrigeren Primärtons, so nimmt der Pegel des kubischen Differenztons wieder ab.

Aus zahlreichen Messergebnissen wird ersichtlich, dass sich die im Gehör erzeugten Differenztöne im Prinzip genauso verhalten wie dem Ohr von außen zugeführte Töne. Als Entstehungsort der Differenztöne wird daher der periphere Teil des Gehörs angenommen.

Beobachtung

Ungeübten fällt es oft schwer, die vorhandenen Töne von den Kombinationstönen zu unterscheiden. Erzeugt man einen konstanten Ton der Frequenz f₁ und überlagert ihm einen Ton ansteigender Frequenz f₂, so fällt die Beobachtung leichter: Neben der Frequenz f₁ und der anwachsenden Frequenz f₂ hört man bei großer Lautstärke leise den quadratischen Kombinationston der Frequenz f₂ − f₁ und noch leiser den kubischen Kombinationston der Frequenz 2 × f₁ − f₂.

Hörbeispiel

Gespielt werden zwei Töne mit den Frequenzen $f_{1}\!$ und $f_{2}\!$ (in Hz):

$f_{1}\!$	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440
$f_{2}\!$	440	466	494	523	554	587	622	659	698	740	784	831	880	932	988	1047	1109	1175	1245	1319	1397	1480	1568	1661	1760

Wenn Sie dieses laut abspielen, hören Sie leise die quadratischen und noch leiser die kubischen Differenztöne.

Im folgenden Beispiel sind zur Verdeutlichung die quadratischen Kombinationstöne mit den Frequenzen $f_{2}-f_{1}\!$ verstärkt. (Den quadratischen Kombinationston hört man von der Tiefe kommend aufsteigend.)

$f_{1}\!$	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440
$f_{2}\!$	440	466	494	523	554	587	622	659	698	740	784	831	880	932	988	1047	1109	1175	1245	1319	1397	1480	1568	1661	1760
$f_{2}-f_{1}\!$	0	26	54	83	114	147	182	219	258	300	344	391	440	492	548	607	669	735	805	879	957	1040	1128	1221	1320

Im folgenden Beispiel sind zur Verdeutlichung die kubischen Kombinationstöne mit den Frequenzen $|2\cdot f_{1}-f_{2}|$ verstärkt. (Den kubischen Kombinationston hört man zuerst tiefer werdend und dann wieder aufsteigend.)

$f_{1}\!$	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440	440
$f_{2}\!$	440	466	494	523	554	587	622	659	698	740	784	831	880	932	988	1047	1109	1175	1245	1319	1397	1480	1568	1661	1760
$\|2\cdot f_{1}-f_{2}\|$	440	414	386	357	326	293	258	221	182	140	96	49	0	52	108	167	229	295	365	439	517	600	688	781	880

Ursachen

Insbesondere bei Frequenzen oberhalb von 1600 Hertz kann das menschliche Gehör nicht mehr die genaue Zeitfunktion der Schallsignale erfassen, sondern nur noch deren Hüllkurve. Die Auswertung ergibt eine Schwingung mit der Frequenz des Differenztons.

Des Weiteren können auch nichtlineare Verzerrungen in der Schallquelle selbst, also dem Schallwandler, dem Instrument oder im Ohr eine Rolle spielen.

Konsequenzen für Musiker

Den Effekt der Kombinationstöne machen sich Musiker beim Stimmen von Instrumenten zunutze, bei denen die Tonerzeuger (z. B. Saiten, Pfeifen) im Abstand einer reinen Quinte zu stimmen sind. Der Differenzton klingt dann nämlich genau eine Oktave unter dem tieferen Tonerzeuger.

Aus dem Phänomen „Kombinationston“ ergeben sich aber auch Konsequenzen für die Musiktheorie. Vergleicht man die große Terz in reiner Stimmung und in gleichstufiger Stimmung, so bemerkt man bei der gleichstufigen Stimmung eine Rauigkeit, die durch den Differenzton noch verstärkt wird. Bei der reinen großen Terz liegt der Differenzton genau zwei Oktaven unter dem tieferen Ton, bei der gleichstufigen Stimmung dagegen um einen Halbton höher, was eine Dissonanz zum Intervallklang ergibt.^[4]

	rein zuerst nur c″e″ (Frequenzen 528 Hz und 660 Hz) dann mit Differenzton C (132 Hz)	gleichstufig zuerst nur c″e″ (Frequenzen 528 Hz und 665,24 Hz) dann mit Differenzton Cis (137,24 Hz)^[5]

Siehe auch

Literatur

Angela Lohri: Kombinationstöne und Tartinis »terzo suono« Verlag Schott Campus 2016, ISBN 978-3-95983-080-5 Printversion und PDF-Download (102 MB)
Eberhard Zwicker: Der ungewöhnliche Amplitudengang der nichtlinearen Verzerrungen des Ohres. In: Acustica. 5, 1955, ISSN 0001-7884, S. 67–74.
Adrian Wehlte: Trios zu zweit (Trios mit 2 Flöten und Kombinationston, Erläuterungen und praktische Übungen zur reinen Intonation) Tibia Heft 2/2012 Moeck-Verlag, Celle 2012, ISSN 0176-6511 und Praxishefte

Einzelnachweise und Anmerkungen

↑ De' Principj dell'armonia musicale contenuta nel diatonico genere. Dissertazione. Padua 1767, darin auf S. 36: "Nell'anno 1714, giovine di anni 22, incirca scopre fortunatamente sul Violino questo fenomeno in Ancona, dove non pochi ricordevoli testimonj sopravvivono ancora."
↑ Anweisung zur Stimmung und Temperatur sowohl der Orgelwerke, als auch anderer Instrumente, sonderlich aber des Claviers, Digitalisat S. 41
↑ Oliver Lehrbaß: Gehörphysiologie und otoakustische Emissionen. 2007, ISBN 978-3-638-79771-9, S. 82. (online)
↑
Bei Hermann von Helmholtz kann dazu nachlesen, dass die gleichstufige Stimmung – bei ihm gleichschwebend genannt – sich von der pythagoreischen Stimmung fast unhörbar unterscheidet. S. 508 „Diese schlechten Kombinationstöne [gemeint sind die Terzen] sind mir immer das Quälendste gewesen in der Harmonie der gleichschwebenden Stimmung […] bilden einen abscheulichen Grundbass dazu.“ S. 510 „Der Hauptfehler unserer gegenwärtigen temperierten Stimmung liegt also nicht in den Quinten; denn deren Unreinheit ist nicht der Rede wert […] Der Fehler liegt vielmehr in den Terzen.“ Ross W. Duffin schreibt dazu (frei übersetzt und zusammengefasst): S. 27 Bei der gleichstufigen Stimmung werden die Quinten angepasst (statt 702 Cent eben 700 Cent) […] und damit ist die Geschichte für viele Schreiber und Musiker zu Ende – außer, dass dieses System der 12 gleichen Halbtöne auf schreckliche Weise die musikalische Harmonie vereinfacht. Denn viele heutige Musiker bemerken dabei nicht, wie schrecklich die große Terz bei gleichstufiger Stimmung klingt (Dort beträgt die Abweichung 14 Cent, ein siebtel Halbton). Dieses Intervall ist der unsichtbare Elefant in unserem System. Quellen:
- Hermann von Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik. Vieweg, Braunschweig 1863, Nachdruck: Minerva-Verlag, Frankfurt/Main 1981, ISBN 3-8102-0715-2 excerpt
- Ross W. Duffin: How Equal Temperament Ruined Harmony (And Why You should Care). Verlag W.W. Norton & Company, New York / London 2007 excerpt
↑ Genaugenommen hat Cis die Frequenz von 137,5 Hz, wobei mit den Frequenzverhältnissen ^C⁄_A = ¹³²⁄₁₁₀ = ⁶⁄₅ (kleine Terz) und ^Cis⁄_A = ^137,5⁄₁₁₀ = ⁵⁄₄ (große Terz) gerechnet wird. Der Unterschied zwischen 137,5 Hz und 137,24 Hz ist allerdings nur 3 Cent, also vernachlässigbar.

[1] De' Principj dell'armonia musicale contenuta nel diatonico genere. Dissertazione. Padua 1767, darin auf S. 36: "Nell'anno 1714, giovine di anni 22, incirca scopre fortunatamente sul Violino questo fenomeno in Ancona, dove non pochi ricordevoli testimonj sopravvivono ancora."

[2] Anweisung zur Stimmung und Temperatur sowohl der Orgelwerke, als auch anderer Instrumente, sonderlich aber des Claviers, Digitalisat S. 41

[3] Oliver Lehrbaß: Gehörphysiologie und otoakustische Emissionen. 2007, ISBN 978-3-638-79771-9, S. 82. (online)

[4] Bei Hermann von Helmholtz kann dazu nachlesen, dass die gleichstufige Stimmung – bei ihm gleichschwebend genannt – sich von der pythagoreischen Stimmung fast unhörbar unterscheidet. S. 508 „Diese schlechten Kombinationstöne [gemeint sind die Terzen] sind mir immer das Quälendste gewesen in der Harmonie der gleichschwebenden Stimmung […] bilden einen abscheulichen Grundbass dazu.“ S. 510 „Der Hauptfehler unserer gegenwärtigen temperierten Stimmung liegt also nicht in den Quinten; denn deren Unreinheit ist nicht der Rede wert […] Der Fehler liegt vielmehr in den Terzen.“ Ross W. Duffin schreibt dazu (frei übersetzt und zusammengefasst): S. 27 Bei der gleichstufigen Stimmung werden die Quinten angepasst (statt 702 Cent eben 700 Cent) […] und damit ist die Geschichte für viele Schreiber und Musiker zu Ende – außer, dass dieses System der 12 gleichen Halbtöne auf schreckliche Weise die musikalische Harmonie vereinfacht. Denn viele heutige Musiker bemerken dabei nicht, wie schrecklich die große Terz bei gleichstufiger Stimmung klingt (Dort beträgt die Abweichung 14 Cent, ein siebtel Halbton). Dieses Intervall ist der unsichtbare Elefant in unserem System. Quellen:
Hermann von Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik. Vieweg, Braunschweig 1863, Nachdruck: Minerva-Verlag, Frankfurt/Main 1981, ISBN 3-8102-0715-2 excerpt

Ross W. Duffin: How Equal Temperament Ruined Harmony (And Why You should Care). Verlag W.W. Norton & Company, New York / London 2007 excerpt

[5] Hermann von Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik. Vieweg, Braunschweig 1863, Nachdruck: Minerva-Verlag, Frankfurt/Main 1981, ISBN 3-8102-0715-2 excerpt

[6] Ross W. Duffin: How Equal Temperament Ruined Harmony (And Why You should Care). Verlag W.W. Norton & Company, New York / London 2007 excerpt

[5] Genaugenommen hat Cis die Frequenz von 137,5 Hz, wobei mit den Frequenzverhältnissen ^C⁄_A = ¹³²⁄₁₁₀ = ⁶⁄₅ (kleine Terz) und ^Cis⁄_A = ^137,5⁄₁₁₀ = ⁵⁄₄ (große Terz) gerechnet wird. Der Unterschied zwischen 137,5 Hz und 137,24 Hz ist allerdings nur 3 Cent, also vernachlässigbar.

[1]

[2]

[3]

[4]

[5]