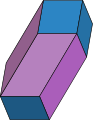
Zonotop
Ein Zonotop bezeichnet in der Geometrie die Minkowski-Summe von Strecken (der Generatoren des Zonotops). Es ist also ein Zonotop im d-dimensionalen Raum, falls Vektoren mit d Einträgen sind.
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]Ein Zonotop ist immer ein konvexes Polytop, und nach der hier gewählten Definition ist der Ursprung das Zentrum des Zonotops. Jedes Zonotop ist punktsymmetrisch zu seinem Zentrum. Jede Facette eines Zonotops ist wiederum ein Zonotop. Das obige Zonotop ist eine Projektion des k-dimensionalen Einheitswürfels in den d-dimensionalen Raum, also in Matrixnotation , wobei die Matrix mit den Generatoren als Spalten eine Projektion und den Einheitswürfel darstellt.
Zonoeder
[Bearbeiten | Quelltext bearbeiten]Ein Zonotop im 3-dimensionalen Raum wird als Zonoeder bezeichnet. Dabei wird meist vorausgesetzt, dass sich das Zonoeder nicht auf eine Ebene beschränkt, die Generatoren also nicht koplanar sind.
Konstruktion eines Zonoeders
[Bearbeiten | Quelltext bearbeiten]Ecken, Kanten und Facetten eines Zonoeders können aus den Generatoren konstruiert und dann zum Beispiel graphisch dargestellt werden. Dabei ist die rekursive Konstruktion besonders anschaulich: Zu einem bereits konstruierten Zonoeder wird eine neue Strecke hinzuaddiert. Zum Beispiel soll zum bereits konstruierten 3-dimensionalen Einheitswürfel das Segment mit hinzuaddiert werden. Dazu wird der Würfel entlang der Kanten aufgeschnitten, die das Segment berühren. Danach werden die Hälften jeweils um den Vektor und verschoben und die entstandene Lücke durch die neue Zone geschlossen.
-
Würfel aufschneiden
-
Hälften heben
-
Lücke füllen
Beispiel
[Bearbeiten | Quelltext bearbeiten]Das Zonoeder mit den Generatoren
stellt den Oktaederstumpf  dar.
dar.
Literatur
[Bearbeiten | Quelltext bearbeiten]- Harold Scott MacDonald Coxeter: Regular Polytopes. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 27–30.
- David Eppstein: Zonohedra and zonotopes. In: Mathematica in Education and Research. 5. Jahrgang, Nr. 4, 1996, S. 15–21 (uci.edu).
Weblinks
[Bearbeiten | Quelltext bearbeiten]- The Geometry Junkyard: Zonohedra and Zonotopes auf ics.uci.edu
- Online Zonotope Builder and Viewer auf decatur.de
![{\displaystyle Z:=[-1,1]v_{1}+\cdots +[-1,1]v_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c88e7d4891bfd57815cdb3f9c60339e80ee53f61)



![{\displaystyle Q:={\begin{pmatrix}[-1,1]\\\vdots \\{}[-1,1]\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2053b25d65ec7461a0811473284f68be27ec9264)

![{\displaystyle [-1,1]v}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b38ff09e908eddd2dd30302fde845e7e9d9d392c)