Espirógrafo

Para el aparato médico que registra los movimientos respiratorios, véase Neumógrafo.

Espirógrafo
Modelo de espirógrafo
Inventor	Denys Fisher
Origen	Reino Unido
Compañía	Hasbro
Disponibilidad	1965-actualidad
Materiales	Plástico
Algunos gráficos diseñados con un espirógrafo
Hasbro
[editar datos en Wikidata]

Animación de un espirógrafo

El espirógrafo^[1]​ es un juguete para generar diseños geométricos. Permite dibujar curvas matemáticas conocidas como hipotrocoides y epitrocoides. El término también ha sido usado para describir varias aplicaciones de informática que muestran curvas similares. Con el nombre comercial de Spirograph, es un producto registrado por la compañía multinacional juguetera Hasbro, Inc.

Historia

Aunque los matemáticos de la antigua Grecia conocían distintas formas de la cicloide, como los epiciclos que utilizó Apolonio de Perga en el siglo III a. C. para explicar el movimiento de los planetas desde un punto de vista geocéntrico, el primer estudio sistemático de las curvas generadas por la trayectoria de una rueda que gira dentro de la circunferencia de otra rueda fue obra del pintor y matemático alemán Alberto Durero en 1525. Durero incluyó la descripción de estas curvas en su manual de geometría en cuatro volúmenes, titulado Instrucciones para la medición, con regla y compás, de líneas, planos y cuerpos sólidos (1538), obra dedicada a las matemáticas y su aplicación a las artes (describe en particular el folium de Durero o epitrocoide).^[2]​

Entre 1845 y 1848, el arquitecto, ingeniero y músico inglés Peter Hubert Desvignes (1804-1883), mientras ejercía su oficio en Viena (Austria), desarrolló el Spirograph, un utensilio destinado a producir guilloché (espirales de patrones compuestos y formas geométricas complejas,^{[nota 1]}​ con el fin de proteger de las falsificaciones documentos como papel moneda, títulos y otros certificados).^[3]​^[4]​

El espirógrafo moderno se debe al matemático e ingeniero polaco Bruno Abakanowicz, quien lo inventó en 1885, durante el desarrollo de instrumentos matemáticos para calcular áreas delimitadas por una curva (conocidos como intégrafos).^[5]​

Los juguetes basados en engranajes para dibujar espirales circulares han existido desde, al menos, 1908, año en que apareció anunciado "The Marvelous Wondergraph" en el catálogo de los Almacenes Sears. Por otro lado, en 1913 la revista "The Boy Mechanic"^[6]​publicó un artículo que describía la construcción de una máquina de dibujo Wondergraph.

El filósofo, matemático e inventor alsaciano Ernst Barthel (1890-1953) patentó en 1933 un dispositivo de dibujo precursor del espirógrafo, denominado «Círculo de transformación» (Transformationszirkel, en alemán), que permite generar curvas a medio camino entre epitrocoides e hipotrocoides.^[7]​

El ingeniero británico Denys Fisher^[8]​ solicitó una patente sobre el juguete el 27 de julio de 1964, siéndole otorgada la patente (N° IE28248 L) el 25 de enero de 1965.^[9]​ Fisher presentó su espirógrafo en la Feria Internacional del Juguete de Núremberg de 1965, y los derechos de distribución fueron adquiridos por la empresa Kenner Products, que introdujo el juego en el mercado estadounidense en 1966.

El nombre “Spirograph” es una marca registrada por la empresa estadounidense Hasbro desde 1998, tras la adquisición en 1970 de la compañía "Denys Fisher Toys". Durante los años 1980, Denys Fisher continuó trabajando con Hasbro en el desarrollo y mejora del juguete.

En 2013, la empresa estadounidense "Kahootz Toys" relanzó en todo el mundo la marca Spirograph con nuevas configuraciones del producto.

Operación

El espirógrafo es un juguete que permite generar diseños geométricos. Con él, puedes dibujar curvas matemáticas conocidas como hipotrocoides y epitrocoides

Un espirógrafo consiste en un conjunto de engranajes de plástico y otras formas como anillos, triángulos, o barras rectas. Existen varios tamaños y formas de engranajes, y todas las extremidades poseen dientes para encajarse en otras piezas. El ajuste de las piezas puede ser, por ejemplo, engranajes pequeños dentro de ruedas mayores u otras muchas combinaciones de las distintas piezas existentes.

Introduciendo la punta de un útil de dibujo por uno de los orificios de una cualquiera de las piezas móviles, y haciéndolas rodar por el interior de un círculo dentado, se obtienen dibujos de distintos patrones festoneados de cicloide.

Imágenes

Evolución de una típica construcción en un espirógrafo

Espirógrafo, un juguete producido y vendido en la URSS en 1980

Razón geométrica

La razón geométrica por la que se pueden trazar las figuras de un espirógrafo es la hipocicloide, en la cual, partiendo de una circunferencia fija, directriz, y otra circunferencia escrita, generatriz, en la directriz y que giran sin deslizar, un punto de la generatriz genera una curva, hipocicloide.

Si perdida del caso general consideremos que en un principio, las dos circunferencias son tangentes el punto más alto y que giran en el sentido de las agujas del del reloj.

La directriz con centro ${\displaystyle O}$ el punto ${\displaystyle A}$ de la directriz es el punto inicial de tangencia con la generatriz. El radio de la directriz lo llamaremos ${\displaystyle g}$:

${\displaystyle {\overline {OA}}=d}$

El punto ${\displaystyle B}$ de la directriz, es el punto de tangencia en cada instante.

La generatriz con centro en ${\displaystyle O'}$ el punto inicial de tangencia de la generatriz con la directriz ${\displaystyle A'}$, el radio de la generatriz lo representamos como: ${\displaystyle g}$

${\displaystyle {\overline {O'A'}}=g}$

El punto ${\displaystyle B'}$ de la generatriz, es el punto de tangencia en un instante dado durante la rotación.

Medido sobre la directriz el arco ${\displaystyle {\overset {\frown }{AB}}}$ tiene una longitud:

${\displaystyle {\overset {\frown }{AB}}=a\cdot d}$

Sobre la circunferencia generatriz ${\displaystyle {\overset {\frown }{A'B'}}}$ tiene una longitud:

${\displaystyle {\overset {\frown }{A'B'}}=b\cdot g}$

Como las circunferencias giran sin deslizar, tenemos:

${\displaystyle {\overset {\frown }{AB}}={\overset {\frown }{A'B'}}\quad \longrightarrow \quad a\cdot d=b\cdot g}$

La posición en el plano del punto ${\displaystyle A'}$ tiene por coordenadas, para un a dado:

${\displaystyle b={\cfrac {a\cdot d}{g}}}$

${\displaystyle x=(d-g)\sin(a)-g\cdot \sin(b-a)}$

${\displaystyle y=(d-g)\cos(a)+g\cdot \cos(b-a)}$

Para un punto distinto de ${\displaystyle A'}$ pero sobre la misma recta a una distancia ${\displaystyle t}$ de ${\displaystyle O'}$, tenemos:

${\displaystyle b={\cfrac {a\cdot d}{g}}}$

${\displaystyle x=(d-g)\sin(a)-t\cdot \sin(b-a)}$

${\displaystyle y=(d-g)\cos(a)+t\cdot \cos(b-a)}$

Ejemplo de espirógrafos

Un espirógrafo de 20cm, ya mencionado como juguete producido y vendido en la URSS en 1980, puede generar los siguientes dibujos.

Un espirógrado del tipo: The original spirograph design set, puede generar dibujos como estos:

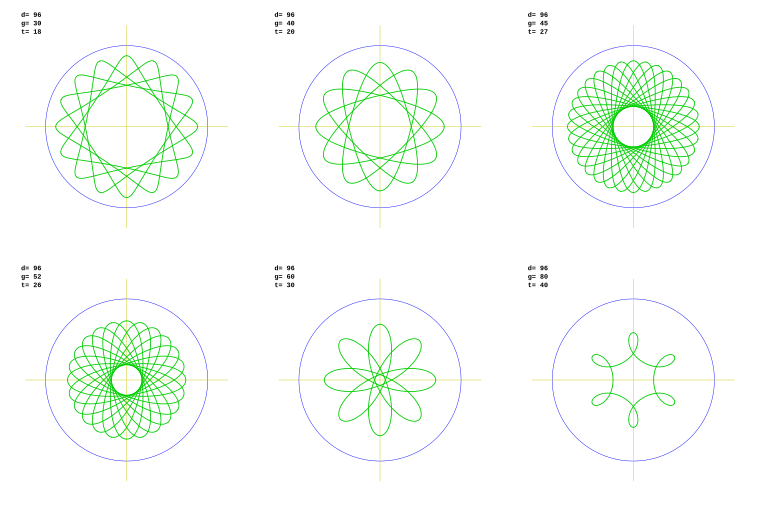
Un espirógrafo que podemos plantear sería el siguiente, con una directriz de 70 y generatrices de: 10, 20, 30, 40, 50 y 60.

Véase también

• Hipocicloide
• Epicicloide
• Epitrocoide
• Guilloché
• Nebulosa del Espirógrafo
• Bruno Abdank-Abakanowicz

Notas

1. El Museo de Ciencias de Londres ha conservado en sus colecciones desde 1886 una copia del Spirograph de Peter Hubert Desvignes, acompañado de muestras de los complejos patrones producidos por su máquina.

Referencias

1. Jorge Lucendo (2019). 80 Siglos de Invenciones: Diccionario de los Inventos. Jorge Lucendo. p. 472. Consultado el 4 de abril de 2021. 
2. Robert Ferréol (1525). «Folium de Dürer». mathcurve.com. Consultado el 18 de enero de 2019. .
3. Science Museum Group (1886). «Spirograph and examples of patterns drawn using it». collection.sciencemuseum.org.uk (en inglés). Consultado el 16 de enero de 2019. .
4. Susan McBurney (2007). «The Spirograph and Beyond» (pdf). archive.bridgesmathart.org (en inglés). Consultado el 16 de enero de 2019. .
5. Rehseis. «Spirographe (Abdank-Abakanowicz, Barbier)». irem.univ-reunion.fr. Archivado desde el original el 14 de enero de 2019. Consultado el 14 de enero de 2019. .
6. F.E. Tuck, Popular Mechanics Press (1913). «From The Boy Mechanic (1913) (How to make a Wondergraph)». marcdatabase.com (en inglés). Archivado desde el original el 30 de septiembre de 2011. Consultado el 15 de enero de 2019. .
7. Innovations & Simulationsservice Festenberg (22 de noviembre de 2014). «Der Barthel'sche Transformationszirkel». festenberg.com (en alemán). Consultado el 17 de enero de 2019. .
8. BoardGameGeek. «Denys Fisher». boardgamegeek.com (en inglés). Consultado el 14 de enero de 2019. .
9. Denys Fisher (25 de enero de 1965). «IE28248 L Design Instrument». worldwide.espacenet.com (en inglés). Consultado el 14 de enero de 2019. .

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Espirógrafo.
• Weisstein, Eric W. «Spirograph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Experimento Epiciclos — aplicación web y galería de imágenes.
• Inspirograph — aplicación web
• Spirograph art creator — aplicación web
• Spirograph — aplicación web java
• Spirograph — software en javascript y AFLAX/flash