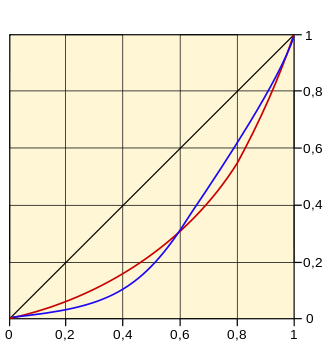
Lorenzen kurba

Errentaren banaketari buurzko Lorenzen kurba bat: errenta txikieneko banakoen % 40ek errenta osoaren % 20 bakarrik jasotzen dute; % 80ek errenta osoaren % 60 jasotzen dute.

Lorenzen kurba guztirako baten banaketa-datuen kontzentrazioaren egitura aztertzen duen estatistika tresna da, batez ere errentaren banaketaren azterketan baina banaketa bat gertatzen den egoera guztietan ere erabil daitekeena^[1]. Zehatzago, banakoen ehuneko bakoitzeko guztirako batetik banako horiek hartzen duten ehunekoa irudikatzen du (adibidez, biztanle guztien %80 pobreenak baliabide guztien % 20 bakarrik hartzen duela aipatzean, Lorenzen kurbako puntu bat adierazten da). Lorenzen kurbatik, gainera, banaketaren kontzentrazio edo ezberdintasunaren neurri batzuk eratortzen dira, Giniren koefizientea esaterako. 1907an Max O. Lorenz ekonomialariak garatu zuen errentaren banaketa aztertzeko, 1905 Leo Chiozza Money politikariak Riches and Poverty bere liburuan horren berri eman bazuen ere ^[2].

Eraketa

Eraketarako, txikienetik handienera ordenatutako x₁, x₂,...,x_n datuetatik abiatu behar da. Datu horiek metatu egiten dira, x₁, x₂,...,x_n balioak sortuz. Metatu gabeko datuen batura, banatzen den guztirakoa alegia, kalkulatzen da. Balio horiek guztirakoarekin zatituz, q_i direlakoak lortuko dira, hots, elementu-multzo bakoitzak kopuru osotik hartzen duen proportzioak.

Beste alde batetik, 1, 2,...,n balioak metatu behar dira, modu erlatiboan, n balioarekiko p_i balioak sortzen dira horrela. Balio horiek elementu-multzo bakoitzak elementu-kopuruarekin duen proportzioak ematen dituzte.

p_i, q_i balioak x,y koordenatu-ardatzetan ezarriz eta puntuak lotuz, (0,0) puntutik abiatu eta (1,1) puntuan bukatuta, Lorenzen kurba irudikatuko da.

Adibidez, banakoen errentari buruzko inkesta batean lortutako datuak direla lehen zutabean agertzen direnak, batura edo guztirako errenta 1 + 1 + ... + 13 = 40 izanik. Errenta horien kontzentrazioa agertzen duen Lorenzen kurba osatzeko, errentak txikienetik handienera metatu eta guztirako errentarekin errenta metatu bakoitzak duen proportzioa kalkulatzen da (adibidez, bigarren lerroan 2/40 = 0,05). Azken zutabean, banako multzo bakoitzak osatzen duen laginaren proportzioa kalkulatzen da (laugarren lerroan, lau banako metatu ondoren, lagin osoaren 4/10 = % 40 osatzen da).

xi (errentak)	Xi (errenta metatuak)	qi (% errenta)	pi (% banakoak)
1	1	0.025	0.1
1	2	0.05	0.2
1	3	0.075	0.3
2	5	0.125	0.4
2	7	0.175	0.5
3	10	0.25	0.6
4	14	0.35	0.7
5	19	0.475	0.8
8	27	0.675	0.9
13	40	1	1

Lorenzen kurba. Ohartu erabateko berdintasuna adierazten duen diagonala ere marrazten dela.

Tartetan bildutako datuetarako kalkulurako, ikus Giniren koefiziente artikuluko adibidea.

Lorenzen kurbako p_i, q_i puntuen interpretazioari dagokionez, bostgarren lerroa hartuz adibidez, guztizkotik gutxien hartu duten pertsonen %50ek guztirakotik % 17,5 bakarrik jasotzen dutela esan behar da. Horrela, Lorenzen kurbak guztizkotik gutxien jaso duten ehuneko jakin batek guztizko osotik zenbat hartzen duen adierazten du.

Lorenzen kurbarekin batera, diagonala ere marraztu ohi da, erreferentzia moduan, diagonalak erabateko berdintasun egoera irudikatzen baitu (gutxienekoen % 10ek % 10 hartzen du, % 20k % 20, ...). Lorenz-en kurba diagonaletik zenbat eta urrunago izan, kontzentrazioa oro har handiagoa izango da. Ohartu behar da Lorenzen kurba beti diagonalaren azpitik doala, banaketa datuak txikienetik handienera ordenatu direlako (adibidez, ez litzateke posible izango da gutxienekoen % 20k % 40 hartzea). Kurbaren malda gero eta handiagoa ere bada, datuak txikienetik handienera metatzen direlako. Horrela, Lorenzen kurbak kontzentrazioaren egituraren azterketa zehatza eta osotua egiteko aukera ematen du, taldeek (gutxienekoen % 5ek ,% 10ek, ...) guztirako batetik zenbat hartzen duten adierazten du, talde jakin batera mugatu gabe.

Lorenzen kurbak erkatuz

Lorenzen kurba bat, bere ibilbide osoan, beste kurba baten gainetik badago, kontzentrazio txikiagoa erakusten du, gutxienekoen ehuneko guztiek guztirakoaren ehuneko altuagoa hartzen dutelako. Lorenzen kurba bi ebakitzen badira, berriz, ezin da esan hain zehatz zein den kontzentrazio handiena erakusten duena.

Kontzentrazioaren egituraren berri ematen badu ere, Lorenzen kurba ez du kontzentrazioaren neurri bakar, orokor eta zehatz ematen. Diagonaletik zenbat eta urrunago izan, kontzentrazioa orduan eta handiagoa bakarrik esan daiteke. Hau dela eta, diagonalaren eta Lorenzen kurbaren arteko azalera hurbiltzen duen Giniren koefizientea erabiltzen da kontzentrazio-neurri moduan.

Lorenzen kurba urdinak kontzentrazio handiagoa erakusten du Lorenzen kurba gorriaren azpitik doalako bere ibilbide osoan.

Lorenzen kurba biak ebaki egiten dira eta ez dago garbi zein den diagonalera bitartean azalera gehien utzi eta, beraz, kontzentrazio handiena duena. Giniren koefizientea kalkulatu behar da azalera horren hurbilketa bat egiteko. Errentaren banaketari buruzko Lorenzen kurbak balira, Lorenzen kurba urdinaren kasuan, errenta txikiko pertsonek arte eta errenta txikiagoa jasotzen dute, ibilbidearen lehenengo zatian urdina azpitik doalako.

Lorenzen kurba probabilitate banakuntzetan

Probabilitate banaketa baterako ere defini daiteke Lorenzen kurba. Probabilitate banaketa jarrai baterako ^[3], ${\displaystyle p,\ L(p)\,}$ puntuak definitutako kurba da, non ${\displaystyle p\,}$ banako edo elementuen proportzioa den, probabilitate metatu bat alegia; eta ${\displaystyle L(p)\,}$ probabilitate horri dagokion aldagaiaren balio metatua den. ${\displaystyle X\,}$ (m-tik M-rako balio posibleak hartzen dituena) zorizko aldagaiaren probabilitate banaketaren trinkotasun-funtzioa eta banaketa-funtzioa ${\displaystyle f_{X}(x)\,}$ eta ${\displaystyle y=F_{X}(x)\,}$ hurrenez hurren hartu eta ${\displaystyle F_{X}^{-1}(x)\,}$ banaketa funtzioaren alderantzizko funtzioa edo koantil-funtzioa izanik^[4]:

${\displaystyle L(p)={\frac {\int _{0}^{p}F_{X}^{-1}(y)dy}{\mu _{X}}}={\frac {\int _{0}^{p}F_{X}^{-1}(y)dy}{\int _{m}^{M}xf(x)dx}};\ \ \ 0<p<1}$

Adibidez, errentak eta, oro har, tamainak modelizatzeko erabiltzen den Paretoren banaketarako honela kalkulatzen da Lorenzen kurba, banaketa-funtziotik abiaturik:

${\displaystyle F_{X}(x)=1-{\Big (}{\frac {x}{\sigma }}{\Big )}^{-\alpha }\ ;\ x>0,\ \alpha >0,\ \sigma >0}$

Haren alderantzizkoa kalkulatuz:

${\displaystyle F_{X}^{-1}(y)=\sigma (1-y)^{\frac {-1}{\alpha }};\ 0<y<1}$

Itxaropen matematikoa hau da:

${\displaystyle \mu _{X}={\frac {\alpha \sigma }{\alpha -1}}}$

Lorenzen kurba azkenik hau da:

${\displaystyle L(p)={\frac {\alpha -1}{\alpha \sigma }}\int _{0}^{p}\sigma (1-y)^{\frac {-1}{\alpha }}dy=1-(1-p)^{1-{\frac {1}{\alpha }}};\ 0<p<1}$

Banakuntza arruntetarako Lorenzen kurbak

Banakuntza	Lorenzen kurba
Uniformea U(a,b)	${\displaystyle L(p)={\frac {2ap+(b-a)p^{2}}{a+b}}}$
Esponentziala [5]	${\displaystyle L(p)=p+(1+{\frac {\mu }{\sigma }}^{-1})(1-p)ln(1-p)}$

Erreferentziak

1. Esaterako, bionaiztasunaren azterketan ere erabilia izan da, espezie ezberdinen artean banakoen banaketa nolakoa den ikertzeko. Wikipedian, ekarpenen kopurua lankide ezberdinen artean nola banatzen den ere aztertzeko erabili da.
2. (Ingelesez) Kleiber, Christian; Kotz, Samuel. (2003). Statistical size distributions in economics and actuarial sciences. , 264 or..
3. Ez da ohikoa Lorenzen kurbaren azterketa probabilitate banaketa diskretuetarako.
4. (Ingelesez) Sarabia, José María. (2008). «Parametric Lorenz Curves: Models and Applications» in Chotikapanich, Duangkamon Modeling Income Distributions and Lorenz Curves. .^{[Betiko hautsitako esteka]}
5. Trinkotasun-funtzio hau duen banaketa esponentzialaren kasuan: ${\displaystyle f(x)=1-e^{-{\frac {(x-\mu )}{\sigma }}}}$.

Ikus, gainera

• Robin Hood adierazlea

Kanpo estekak