Pavage de Penrose

Un pavage de Penrose.

Roger Penrose, debout sur le pavage de Penrose du foyer de l'institut Mitchell, Texas A&M University.

Les pavages de Penrose sont, en géométrie, des pavages du plan découverts par le mathématicien et physicien britannique Roger Penrose dans les années 1970. En 1984, ils ont été utilisés comme un modèle intéressant de la structure des quasi-cristaux.

Définition

Les pavages de Penrose sont des pavages non périodiques caractérisables par des règles locales : s'ils ne sont historiquement pas les premiers à vérifier cette propriété, ils sont parmi les plus simples, et à ce titre largement étudiés (le premier tel pavage, construit par Robert Berger en 1966, comportait 20 426 tuiles).

Les 17 pavages périodiques du plan étaient connus de longue date quand Roger Penrose s'est intéressé aux pavages non périodiques. Son intention n'était pas d'ouvrir un nouveau champ des mathématiques et de la physique mais seulement de créer un divertissement mathématique. En 1974, il publia un article présentant un pavage du plan à l'aide de pentagones, de losanges, de pentagrammes et de portions de pentagrammes^[1].

Certains pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle 2π/5 radian, soit 72°), mais aucun n'est périodique, c'est-à-dire qu'on ne peut le décrire comme un motif répété sur une grille régulière. Ils sont cependant tous quasi périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement. Plus généralement toute portion finie du pavage, aussi grande soit-elle, se répète infiniment dans le pavage.

Les pavages de Penrose ne seraient restés qu'un joli divertissement mathématique si n'avaient été découverts, en 1984, des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodique : les quasi-cristaux. Les pavages non périodiques, en particulier ceux de Penrose, s'avérèrent alors un modèle plausible de ces étranges matériaux.

Cette découverte illustra à nouveau ce que Roger Penrose lui-même avait déjà remarqué en 1973, à propos d’un sujet de relativité générale : « On ne sait jamais vraiment quand on perd son temps »^[2].

Il existe trois types de pavages de Penrose, chacun comportant une infinité de variantes :

• Le premier type, qu'on appelle P1, utilise comme pièces de base des pentagones, des losanges, des pentagrammes et des portions de pentagramme.
• Le second type, ou P2, a pour pièces de base deux quadrilatères, l'un convexe, l'autre concave, connus comme « cerfs-volants » et « fléchettes ».
• Le troisième type, P3, a pour pièces de base deux sortes de losanges, « fins » et « gros ».

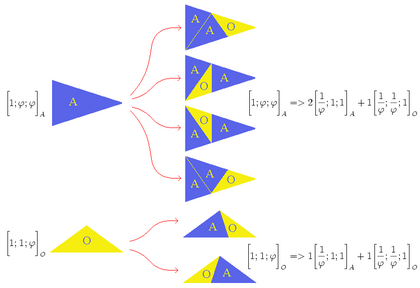
On s'est aperçu que fléchettes, cerfs-volants et losanges peuvent tous être construits à partir d'une paire de triangles d'or. Les pièces de P2, « cerfs-volants » et « fléchettes », sont obtenues respectivement par le collage de deux triangles d'or aigus de côtés proportionnels à [1;φ;φ] et par le collage de deux triangles d'or obtus (ou triangles d'argent) de côtés proportionnels à [1;1;φ]. Celles de P3, les losanges fins et gros, par le collage de deux triangles d'or aigus de côtés proportionnels à [1;φ;φ] et par le collage de deux triangles d'or obtus de côtés proportionnels à [φ;φ;φ²]. Cette série de simplifications permet de considérer les triangles d'or comme prototypes des autres pièces et de dire qu'un type « zéro » précède les autres.

Pavage de Penrose avec triangles d'or (pavage de type 0)

Il existe de nombreuses façons de définir un triangle d'or. L'une des plus simples est la suivante^[3] :

« Un triangle d'or est un triangle isocèle dont les côtés ont des longueurs proportionnelles à [1 ; φ ; φ] ou [1 ; 1 ; φ] où φ est le nombre d'or. »

• Les côtés d'un triangle d'or aigu ont des longueurs proportionnelles à [1 ; φ ; φ]
• Les côtés d'un triangle d'or obtus^[4] ont des longueurs proportionnelles à [1 ; 1 ; φ].

On peut démontrer que ce sont les seuls triangles isocèles vérifiant la propriété ${\displaystyle (P)\,}$ suivante : pouvoir être découpé en deux triangles isocèles inégaux et possédant à leur tour la propriété ${\displaystyle (P)\,}$.

Ces deux types de triangles d'or peuvent s'obtenir en découpant un pentagone régulier :

Les deux types de triangles d'or (A et O).

Chacun de ces types possède un angle ${\displaystyle \alpha \,}$ de 36° (soit π/5 radians), les deux autres angles étant (comme le montre la figure ci-dessus), soit égaux à ${\displaystyle \alpha \,}$, soit multiples de ${\displaystyle \alpha \,}$ (d'un facteur 2 ou 3).

L'angle ${\displaystyle \alpha \,}$ est lié au nombre d'or φ par de nombreuses propriétés ; en effet :

${\displaystyle \cos \alpha =\sin {\frac {3\alpha }{2}}={\frac {\varphi }{2}}\,{\textrm {et}}\ \sin {\frac {\alpha }{2}}=\cos 2\alpha ={\frac {1}{2\varphi }}\,}$

Ils possèdent en outre les propriétés suivantes :

• Tout triangle d'or aigu (A) de dimensions [1 ; φ ; φ] peut se décomposer (de quatre façons différentes, deux à deux symétriques) en trois triangles : un triangle d'or obtus [1/φ ; 1/φ ; 1] et deux triangles d'or aigus [1/φ ; 1 ; 1], ces nouveaux triangles ayant donc, par rapport au triangle d'or générateur, une taille divisée par φ ;
• Tout triangle d'or obtus (O) de dimensions [1 ; 1 ; φ] peut se décomposer (de deux façons différentes et symétriques) en deux triangles : un triangle d'or aigu [1/φ ; 1 ; 1] et un triangle d'or obtus [1/φ ; 1/φ ; 1].

Les diverses possibilités de découpage des deux types de triangles d'or.

Animation montrant comment on peut, avec des triangles d'or, réaliser un pavage de Penrose de type 0 (6 étapes)
(toutefois, l'agrandissement dont il est question dans le texte ci-contre n'a pas été réalisé, afin d'améliorer la visibilité !)

Pavage de Penrose avec des triangles d'or (pavage de type 0).

Ces propriétés peuvent être utilisées pour construire un pavage de Penrose de type 0 :

En découpant un premier triangle d'or (aigu ou obtus, peu importe) et en opérant un agrandissement d'un facteur φ, puis en recommençant l'opération précédente une infinité de fois, on constitue un pavage complet du plan à l'aide des deux types de triangles d'or. Si, à l'étape n, on appelle ${\displaystyle a_{n}\,}$ le nombre de triangles aigus et ${\displaystyle o_{n}\,}$ le nombre de triangle obtus, on observe les formules de récurrence :

${\displaystyle o_{n+1}=o_{n}+a_{n}}$

${\displaystyle a_{n+1}=o_{n}+2a_{n}=o_{n+1}+a_{n}}$

En considérant la suite ${\displaystyle u_{n}}$ définie par

${\displaystyle u_{2n}=o_{n}}$

${\displaystyle u_{2n+1}=a_{n}}$,

on s'aperçoit que cette suite vérifie la relation de récurrence de la suite de Fibonacci

${\displaystyle u_{n+2}=u_{n+1}+u_{n}}$,

suite dont on sait que le rapport de deux termes consécutifs tend vers le nombre d'or φ. Ainsi la valeur limite du rapport du nombre de triangles obtus et du nombre de triangles aigus est un nombre irrationnel, ce qui entraîne que le pavage obtenu de cette façon ne peut pas être périodique.

Pavage avec cerfs-volants et fléchettes (pavage de type 2)

Le pavage précédent a l'avantage de la simplicité mais sa construction n'est pas unique : en effet, chaque découpage d'un triangle peut s'effectuer d'au moins deux façons différentes (symétriques). En outre, ces découpages ne donnent pas une impression de régularité et conduisent donc à des pavages assez peu élégants.

Mais on peut concevoir un autre type de pavage.

Cerf-volant et fléchette.

En réunissant deux triangles d'or aigus ayant pour sommet commun le sommet dont la bissectrice est un axe de symétrie pour les deux autres sommets (sommets correspondant à un angle de 36°), on obtient un « pavé » en forme de cerf-volant. Si on fait la même construction avec deux triangles obtus (sommets correspondant à un angle de 108°), on obtient un « pavé » en forme de fléchette.

On peut alors paver le plan avec ces deux nouveaux « pavés ». En effet, si on prend bien soin de ne jamais accoler une fléchette et un cerf-volant en formant un parallélogramme, on peut construire ainsi un pavage non périodique. Il suffit pour cela de nommer les sommets comme indiqué sur la figure ci-dessus et de se fixer pour règle de n'accoler deux sommets que s'ils portent le même nom. Il existe une infinité de pavages du plan de ce type.

Découpes du cerf volant et de la fléchette.

Mais on peut également, comme pour le pavage à l'aide des triangles d'or, définir un algorithme de « construction par découpage » consistant à chaque étape à découper chaque cerf-volant en deux cerfs-volants et deux demi-fléchettes et une fléchette en un cerf-volant et deux demi-fléchettes, et en agrandissant d'un facteur φ le résultat obtenu (remarquer que les sommets changent de nom à chaque étape, A devenant B et B devenant A).

La cohérence du procédé est assurée par le fait que les demi-fléchettes ainsi générées s'associent toujours avec leur voisine pour reconstituer une fléchette complète (ce qui assure la disparition des lignes en pointillé visibles sur la figure précédente).

Pavage de Penrose avec cerfs-volants et fléchettes.

La figure obtenue au bout de plusieurs itérations laisse déceler une quasi-symétrie d'ordre 5. Il est facile de prouver que, comme pour les triangles d'or, la proportion entre le nombre de cerfs-volants et celui de fléchettes tend vers le nombre d'or φ, ce qui assure que le pavage ainsi construit n'est pas périodique.

À la différence du premier type de pavage, ici la construction par découpage génère un seul type de pavage de type 2 puisque le découpage des cerfs-volants et des fléchettes ne peut être réalisé que d'une seule façon.

Un exemple : trois générations de quatre figures

Voici des exemples de générations successives en partant d'une forme de base. Dans les figures « Soleil » et « Étoile », on retrouve la figure de départ réduite à la deuxième génération. Le « Soleil » apparaît même dans la génération 3.

Nom	Génération 0	Génération 1	Génération 2	Génération 3
Cerf-volant (demi)
Flèche (demie)
Soleil
Étoile

Pavage avec des losanges (pavage de type 3)

Assemblage de losanges dans un pavage de Penrose.

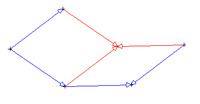
Il est aussi possible de paver le plan à l'aide de deux figures géométriques simples comme les deux losanges suivants. À condition de les assembler en respectant la couleur et le sens des vecteurs. Ces contraintes d'assemblage assurent que le pavage obtenu ne sera pas périodique. Comme précédemment, il existe une infinité de pavages du plan non périodiques à l'aide de ces deux pièces.

Respecter les règles d'assemblage dans la construction manuelle d'un large pavage est difficile : il s'avère que pratiquement toutes les configurations finies, aussi grandes soient-elles, ne peuvent être étendues à l'infini^[5]. Une personne cherchant à paver une grande surface, à la manière d'un puzzle, sera donc fréquemment conduite à une impasse, comme un trou impossible à paver suivant les règles, et devra défaire en partie son assemblage pour retenter un autre pavage.

De plus il n'existe aucun algorithme de croissance locale du pavage qui garantisse que le pavage soit extensible à l'infini. Autrement dit, toutes les méthodes de construction, par ajout de tuiles une à une et qui évitent de conduire à une impasse, prennent nécessairement en compte l'ensemble des tuiles déjà placées^[6].

Découpe des losanges.

Comme pour les autres types de pavage de Penrose, on peut définir aussi un algorithme de « construction par découpage » : il suffit de découper chaque gros losange en un gros losange, deux demi-losanges fins et deux demi-losange gros, et chaque losange fin en deux demi-losange fins et deux demi-losanges gros. La cohérence du procédé est assurée par le fait que les demi-losanges ainsi générés s'associent toujours avec leur voisin pour reconstituer un losange complet (ce qui assure la disparition des lignes en pointillé visibles sur la figure ci-contre).

Pavage en losanges.

Création d'un pavage de Penrose de type 3 par découpes successives.

La figure obtenue au bout de plusieurs itérations laisse déceler une quasi-symétrie d'ordre 5. Il est facile de prouver que, comme pour les triangles d'or, la proportion entre le nombre de gros losanges et celui de losanges fins tend vers le nombre d'or φ. Ce qui assure que le pavage ainsi construit n'est pas périodique.

Pavage dit « pentagonal » (pavage de type 1)

Pavage pentagonal (P1) tracé en noir sur fond vert-bleu de pavage du troisième type (P3).

Le pavage construit autour de pentagones, P1, est en fait le premier découvert par Penrose, qui s'est inspiré d'abord des recherches de Johannes Kepler^[7]. Il est bien connu qu'on ne peut couvrir le plan avec des pentagones réguliers, mais trois autres pièces suffisent pour combler les interstices, tout en imposant l'ordre apériodique. Ces pièces sont un losange fin, un pentagramme et un « bateau », qui représente à peu près les 3/5 d'un pentagramme. Pour la construction directe du pavage apériodique, il faut aussi distinguer trois sortes de pentagones. Une solution bien plus simple consiste à esquisser des pentagones sur les losanges fins et gros qu'on arrange en pavage de type 3.

On peut retrouver directement le pavage par triangles d'or dans le pavage pentagonal, sans utiliser les losanges. Si l'on assigne aux pointes des pentagones successivement les nombres 1, 3, 5, 2, 4, tous les points qui définissent le pavage P3 seront numérotés. Cela peut être fait d'une manière consistante et non équivoque en tournant à gauche ou à droite selon les cas. Choisissant les points qui portent un même numéro, on obtient un pavage de type « zéro ». Le sous-ensemble des points numérotés avec 3 et 4 donne une autre variante de pavage de Penrose, obtenue avec deux pièces connues comme « papillon » et « navette »^[8].

Recouvrement avec des décagones

La mathématicienne allemande Petra Gummelt a prouvé en 1996 qu'un pavage de Penrose pouvait être obtenu en recouvrant le plan uniquement avec des décagones, à condition toutefois que deux types discrets d'empiètement soient permis^[9]. Le décagone proposé est décoré avec cinq cerfs-volants et l'empiètement permis ne change pas la configuration de ces parties coloriées.

Le décagone de Gummelt et ses quatre types d'empiètement.

Il est possible de décomposer le décagone en fléchettes et cerfs volants, réduisant le tableau obtenu en un pavage de Penrose. Le pavage avec des losanges peut être retrouvé directement en gravant un gros losange dans le décagone; les parties laissées en creux seront celles que remplissent les losanges fins. Cette nouvelle façon de procéder a eu un impact considérable sur les conceptions à propos de la formation des quasi-cristaux.

Occurrences

On peut rapporter les occurrences du pavage de Penrose à trois grandes catégories :

• Mathématiques : en fait c'est le seul contexte adéquat pour la considération des pavages de Penrose. Étant des objets non finis, la plupart des assertions à leur sujet n'ont de validité qu'avec preuves à l'appui. L'existence d'un ensemble de « tuiles » apériodique a été démontrée dans les années 1960 et les cas particuliers réduits à deux pièces ont l'avantage d'être parmi les plus simples possibles. Alain Connes a fait des pavages de Penrose un exemple privilégié pour sa géométrie non commutative^{[réf. souhaitée]}.

À un niveau plus élémentaire, on a trouvé de multiples et très étroites relations entre le nombre d'or, les suites de Fibonacci et les pavages de Penrose.

• Physique : l'intérêt des physiciens n'est venu qu'après 1984, quand furent découverts les premiers quasi-cristaux. Assez vite il a été établi que deux types présentent une quasi-symétrie d'ordre 5 : ceux à structure icosaédrique et ceux à structure simplement décagonale. Dans les deux cas il existe des plans où la disposition des atomes donne un pavage de Penrose. Dans leurs travaux les physiciens ont recours à une méthode générale qui permet d'obtenir des pavages non-périodiques à partir de simples grilles dans des dimensions supérieures à 3.
• Art : la valeur esthétique des pavages de Penrose est immédiatement perceptible. On peut supposer que c'est là le même mécanisme psychique qui a amené le développement des entrelacs et autres ornements semblables. Le rapprochement avec les décorations à symétrie centrale d'ordre 5 ou 10 a été fait dès le début de la vogue quasi-cristalline^[10]. À la mosquée de Darb-i Imam à Isfahan, on observe des motifs qui ont permis d'affirmer que les artisans de l'Islam médiéval disposaient de tous les éléments pour construire un pavage de Penrose^[11]. On trouve des motifs faits avec des pentagones et des losanges parmi les esquisses d'Albert Dürer et qui peuvent être mis en connexion avec le travail de Johannes Kepler. Le fragment de pavage qui figure dans Harmonices Mundi peut être prolongé de façon apériodique, ce qui produit un type équivalent à celui de Penrose (P1)^[12]. Roger Penrose a homologué sa découverte comme « un jeu de tuiles pour couvrir des surfaces », en précisant que « l'arrangement qu'elles forment est nécessairement non-périodique, ce qui lui donne un attrait visuel considérable »^[13] et a veillé sur l'utilisation commerciale. Des artistes contemporains (Clark Richert, Jos Leys) se sont inspirés de sa géniale trouvaille.

Notes et références

1. (en) Roger Penrose, « The role of aesthetics in pure and applied mathematical research », Bulletin of the Institute for Mathematics and its Applications, vol. 10,‎ 1974, p. 266-271.
2. La Recherche/Tangente, mai-juin 2000, p 40.
3. Par exemple Jean-Claude Thiénard, Maryse Cheymol, Maryse Combrade et Louis-Marie Bonneval, Mathématiques seconde (lire en ligne), p. 100.
4. Certains auteurs réservent le qualificatif de triangle d'or seulement au triangle d'or aigu et appellent ce triangle un gnomon d'or (voir (en) Eric W. Weisstein, « Golden gnomon », sur MathWorld).
5. (en) Roger Penrose, Aperiodicity and Order, vol. 2, Marko V. Jarić, 1989, p. 53-79 (ISBN 9780120406029, DOI 10.1016/B978-0-12-040602-9.50007-5), « Tilings and Quasi-Crystals; a Non-Local Growth Problem? »
6. (en) Elissa Joanne Ross, Non-local growth of Penrose tilings, B.SC. University of Guelph, 2003 (lire en ligne).
7. (la) Johannes Kepler, Harmonices Mundi, 1619 (lire en ligne).
8. (en) Reinhard Lück, « Penrose Sublattices », Journal of Non Crystaline Solids, vol. 117-8,‎ 1990, p. 832-5 (ISSN 0022-3093, DOI 10.1016/0022-3093(90)90657-8.).
9. (en) Petra Gummelt, « Penrose tilings as coverings of congruent decagons », Geometriae Dedicata, vol. 62,‎ 1996, p. 1–17 (DOI 10.1007/BF00239998, lire en ligne ).
10. (en) Emit Makovicky, Fivefold Symmetry, Singapore-London, I. Hargittai, coll. « World Scientific », 1992, p. 67-86, « 800-year-old pentagonal tiling from Maragha, Iran, and the new varieties of aperiodic tiling it inspired ».
11. (en) Peter J. Lu et Paul J. Steinhardt, « Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture », Science, vol. 315, n^o 5815,‎ 2007, p. 1106-1110.
12. (en) Reinhard Lück, « Dürer–Kepler–Penrose, the development of pentagon tilings », Materials Science and Engineering: A, vol. 294–296,‎ 15 décembre 2000, p. 263-267.
13. Roger Penrose, U.S. Patent 4,133,152 Set of tiles for covering a surface, issued January 9, 1979 (expired,link).

Voir aussi

Bibliographie

• L'aventure des pavages de Penrose Revue Tangente et La Recherche (avril-mai 2000)

Articles connexes

• Pavage apériodique
• Zellige

Liens externes

• « Visualisateur de pavages de Penrose »
• Pavages, sur le site Images des mathématiques du CNRS
• (it) Film (en italien) sur les pavages de Penrose

• Portail de la géométrie
• Portail des sciences des matériaux
• Portail des minéraux et roches