一般相対性理論の概説

カッシーニ宇宙探査機による一般相対性理論の高精度の試験（イメージ図）。地球と探査機の間で送信される無線信号（緑の波）は、太陽の質量による時空の歪み（青線）により遅延する。

一般相対性理論の概論（いっぱんそうたいせいりろんのがいろん）では、アルベルト・アインシュタインにより1907年から1915年の間に発展された重力の理論について説明する。

一般相対性理論によると、質量間の観測される重力効果は時空のゆがみから生じる。

20世紀初頭まで、ニュートンの万有引力の法則は質量間の重力の確実な記述として200年以上にわたり受け入れられていた。ニュートンのモデルにおいては、重力は質量を持つ物体間の引力の結果である。ニュートンでさえその力の未知の性質に苦悩したが、この基本的な枠組みは運動を記述するのに非常に上手くいった。

実験や観測は、アインシュタインの重力の記述が、水星や他の惑星の軌道のわずかな異常などニュートンの法則では説明できないいくつかの効果を説明していることを示している。一般相対性理論は重力波、重力レンズや重力時間膨張として知られる時間に対する重力の影響など、重力の新たな効果を予測する。これらの予測の多くは、実験、観測、近年では重力波により確認されている。

一般相対性理論は現代天体物理学において不可欠な道具に発展した。これにより重力の効果が光でさえも逃げ出すことができないほど強い空間領域であるブラックホールの現在の理解の基礎が提供されている。これらの強い重力は特定の種類の天体（活動的な銀河核やマイクロクエーサーなど）から放出される強い放射の原因であると考えられている。一般相対性理論は宇宙論の標準ビッグバンモデルの枠組みの一部でもある。

一般相対性理論は唯一の重力の相対論的理論ではないが、実験データと矛盾しない最も単純な理論である。それでも多くの未解決の問題が残っており、その中でも最も基本的なものは一般相対性理論は量子物理学の法則とどのように調和し、完全で自己矛盾のない量子重力の理論を生成できるかというものである。

特殊相対性理論から一般相対性理論へ

[編集]

1905年9月、アルベルト・アインシュタインはニュートンの運動法則を電気力学（電荷を持つ物体間の相互作用）と調和させる特殊相対性理論を発表した。特殊相対性理論は空間と時間の新たな概念を提案することにより、物理学の全てに対して新たな枠組みを導入した。当時受け入れられていたいくつかの物理理論はこの枠組みと矛盾していた。鍵となる例は質量により物体が受ける相互引力を説明するニュートンの重力理論である。

アインシュタイン含む何人かの物理学者は、ニュートンの重力法則と特殊相対性理論を調和させる理論を探究し、アインシュタインの理論のみが実験や観測と一致することが分かった。理論の基本的な考えを理解するために、1907年から1915年の自由落下の観測者など単純な思考実験から重力の完全な幾何理論までのアインシュタインの思考を追うことは勉強になることである[1]。

等価原理

[編集]

自由落下するエレベーターに乗っている人は無重量状態を感じる。物体は静止したまま浮遊するか一定速度で漂流する。エレベーター内の全てが一緒に落下しているため、重力効果を観測することができない。このように、自由落下している観測者が経験するものと大きな重力源から遠く離れた深宇宙の観測者が経験するものは区別できない。これらの観測者はアインシュタインが特殊相対性理論において特権的（「慣性」）観測者と書いた者であり、光はこの観測者に対して一定速度で直線に沿って進む[2]。

アインシュタインは、特殊相対性理論における無重力の観測者と慣性の観測者が同様に経験することが重力の基本的性質を現していると仮定し、これを一般相対性理論の基礎として等価原理で定式化した。大まかに言うと、この原理は自由落下するエレベーターにいる人は自由落下していることを知ることはできないというものである。このような自由落下環境における全ての実験は、静止している時や全ての重力源から遠く離れた深宇宙で一様に動いている観測者に対するであろうものと同じ結果になる[3]。

重力と加速度

[編集]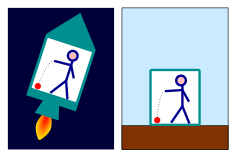
加速するロケット（左）と地球上（右）において床に落ちるボール。効果は同じである。

重力のほとんどの効果は自由落下で消えるが、重力の効果と同じように見える効果は加速された座標系により作り出される。密室にいる観測者は次のどれに該当するか分からない。

  • 部屋は地表上にあり、物体は重力により引き下げられているため、物体が床に落ちている。
  • 部屋が宇宙空間にあり9.81 m/s2 で加速しておりあらゆる重力源から離れているロケット上にあり、物体が床に落ちている。物体は加速する車の運転手を座席の後ろに押す同じ「慣性力」により床に引っ張られる。

逆に、加速される基準系で観測される効果は対応する強度の重力場でも観測される必要がある。次節でも説明するように、アインシュタインはこの原理により1907年に新しい重力の効果を予測することができた。

加速される基準系の観測者は、物理学者が見かけの力と呼ぶものを導入して自分自身と周りの物体が経験した加速を説明する必要がある。一例として加速する車の運転手を座席へ押し込む力についてはすでに述べた。もう一つの例としては頂点のように回転しようとすると腕が上下に引っ張られると感じる力がある。アインシュタインの主な洞察は、一定の身近な地球の重力場の引き寄せる力は、これらの見かけの力と基本的に同じであるというものであった[4]。見かけの力の大きさは常にそれが作用する物体の質量に比例するように見える。例えば、運転席は車と同じ速度で運転者を加速させるのに十分な力を働かせる。アインシュタインは類推により重力場にある物体は、ニュートンの重力法則で具体化されているようにその質量に比例した重力を感じるべきだと提案した[5]。

物理的結果

[編集]

1907年の段階ではアインシュタインは一般相対性理論の完成まで8年を残していたが、新たな理論を発展するための出発点である等価原理に基づいた新しい検証可能な予測を多く行うことができた[6]。

光波が重力場に対して上方に動くときの光の重力の赤方偏移（下の黄色の星により起こされる）

最初の新たな効果は、光の重力周波数シフトである。加速するロケット船に乗っている2人の観測者を想定する。このような船に乗ると「上」と「下」という自然な概念がある。船が加速する方向は「上」であり、くっついていない物体は反対方向に加速し「下向き」に落ちる。観測者の1人がもう1人よりも「高い」と仮定する。低いところの観測者が高いところの観測者へ光信号を送信すると特殊相対性理論から計算されるように、加速度により光が赤方偏移し、2番目の観測者は最初の観測者よりも低い周波数の光を測定する。逆に、高い観測者から低い観測者に送られる光は青方偏移、つまり高い周波数にシフトする[7]。アインシュタインは、このような周波数シフトは重力場でも観測される必要があると主張した。これは左図に示されている。これは、重力加速度に逆らって上方向に進むにつれて徐々に赤方偏移する光波を示している。以下に説明するようにこの効果は実験的に確認されている。

この重力による周波数シフトは重力による時間の遅れに対応する。「高い」観測者は「低い」観測者よりも低い周波数を持つように同じ光波を測定するため、高い観測者に対しては時間が早く経過しなければならない。したがって、重力場において低い観測者の時間は遅く過ぎていく。

各々の観測者について、自身の基準系内で静止している事象もしくは過程に対する時間の流れに観測可能な変化がないことを強調することは重要である。各観測者の時計で計時される5分卵(five-minute-eggs)は 同じ一貫性を持つ。各時計で1年がたつと各観測者はその分老ける、つまり、各時計はその近くで発生する全ての過程と完全な一致を見る。別の観測者間で時計が比較されるときのみ、高い観測者よりも低い観測者の方が時間の進みが遅いことに気づくことができる[8]。この効果は微小であるが、以下で記述されるように複数の実験で実験的に確認されている。

アインシュタインは同様の方法で重力による光のゆがみを予測した。重力場においては、光は下向きにゆがむ。定量的には、彼の結果は2分の1であった。正しい導出には等価原理だけでなく一般相対性理論のより完全な定式化を要する[9]。

潮汐効果

[編集]
地球の中心に向かって落下する2つの物体は、落下するにつれて互いに向かって加速する。

重力効果と慣性効果の等価性は、重力の完全な理論を構成するものではない。地表上の自分の位置近くで重力を説明する場合、基準系が自由落下していないことに注意し見かけの力を予期することで、適切な説明が提供される。しかし、地球のある側で自由落下する基準系は、地球の反対側の人々が反対方向に引っ張る重力を経験する理由を説明できない。

同じ効果のより基本的な表れには、地球に向かって並んで落下している2つの物体が含まれる。これらの物体と並んで自由落下している基準系においては、無重力で空間に停止しているように見えるが、正確にはそうではない。これらの物体は正確に同じ方向に落ちるのではなく、空間内の1つの点、地球の重心に向かって落下する。結果としてもう1つの物体に向かう各物体の運動の成分がある（図参照）。自由落下するリフトなどの小さな環境ではこの相対加速度は非常に小さく、地球の反対側のスカイダイバーにとっては効果が大きくなる。これらの力の違いは地球の海の潮汐の原因でもあるため、この現象には「潮汐効果」という名前が使われている。

慣性と重力の等価性では潮汐効果を説明できない。重力場の変動を説明できないからである[10]。これを説明するためには、物質（地球の大きな質量など）が周囲の慣性環境に影響を及ぼす方法を説明する理論が必要である。

加速度から幾何へ

[編集]

重力と加速度の等価性、および潮汐力の役割を探究する中で、アインシュタインは表面の幾何学との類似性をいくつか発見した。1つの例は慣性基準系（自由粒子が一定速度で直線経路に沿って滑走する）から回転基準系（粒子の運動を説明するために見かけの力に対応する追加の項を導入する必要がある）への移行である。これはデカルト座標系（座標線が直線）から曲線座標系（座標線が直線である必要はない）への移行と類似している。

より深みを持つ類似は潮汐力を曲率と呼ばれる表面の性質と関連付ける。重力場の場合、潮汐力の有無が、自由落下する基準系を選択することにより重力の影響を取り除くことができるかどうかを決定する。同様に曲率の有無が表面が平面と同等であるかどうかを決定する。1912年の夏、これらの類似にインスピレーションを受け、重力の幾何学的定式化を探究した[11]。

幾何学の基本的な物体（点、線、三角形）は伝統的に3次元空間もしくは2次元表面で定義される。1907年、スイス工科大学でアインシュタインの数学教授を務めていたヘルマン・ミンコフスキーはアインシュタインの特殊相対性理論の幾何学的定式化を導入した。ここには空間だけでなく時間も含まれていた。この新しい幾何学の基本的な実体は4次元時空である。動く物体の軌道は時空の曲線である。方向を変えずに一定速度で移動する物体の軌道は直線に対応する[12]。

表面については、19世紀初頭にカール・フリードリヒ・ガウスにより平面の幾何学から一般的な曲面の幾何学への一般化が記述されていた。この記述は1850年代にベルンハルト・リーマンにより導入された数学的形式主義における高次元空間に一般化された。アインシュタインはリーマン幾何学の助けを借りて重力の幾何学的記述を定式化した。ここでは曲面が通常の平面の一般化であるようにミンコフスキーの時空が歪んで曲がった時空に置き換えられる。埋め込み図は、教育の文脈で曲がった時空を説明するのに使われる[13][14]。

アインシュタインはこの幾何学的類推の妥当性に気づいたのち、欠けている理論の礎石、物質が時空の曲率にどのように影響するかを記述する方程式を見つけ出すのに3年を要した。今日アインシュタイン方程式（より正確にはアインシュタインの重力場方程式）として知られているものを定式化したのち、1915年後半にプロイセン科学アカデミーのいくつかのセッションで自身の重力の理論を発表し、1915年11月15日の最終プレゼンで最高潮に達した[15]。

幾何学と重力

[編集]

ジョン・ホイーラーを言い換えると、アインシュタインの重力の幾何学理論は次のように要約できる: 時空は物質にどのように動くかを伝え、物質は時空にどのように曲がるかを伝える[16]。これが意味することは次の3つのセクションで処理される。これらのセクションでは、いわゆる試験粒子の運動を調べる、物質のどの特性が重力源として機能するかを調べる、最後にアインシュタイン方程式に導入されることでこれらの物質の特性を時空の曲率と関連付ける。

重力場の調査

[編集]
集束測地線: 赤道（赤線））において平行である2本の経度線（緑線）は極で1点に集まる。

物体の重力の影響をマッピングするために、物理学者がプローブもしくは試験粒子と呼ぶものを考えるのは有用である: 粒子は重力の影響を受けるが、非常に小さく軽いため自身の重力効果を無視できる。重力やその他の外力がない場合、試験粒子は一定速度で直線に沿って移動する。時空の言葉では、このことは試験流が時空の直線の世界線に沿って移動するということと同等である。重力がある場合、時空は非ユークリッド、曲であり、曲がった時空では直線の世界線は存在しない場合がある。代わりに、試験粒子は測地線と呼ばれる線に沿って移動する。測地線とは「可能な限り直線」であり、試験粒子は曲率を考慮して始点と終点の間の最短経路をたどる。

単純な類似は以下の通りである。測地学（地球の大きさと形状を測定する科学）において測地線（英語のgeodesicはギリシア語で地球を意味する"geo"と分割を意味する"daiein"に由来）は地表上の2点間の最短ルートである。およそこのようなルートは経線や赤道などの大円の部分である。これらの経路はたしかにまっすぐではない。というのは、単に地表の曲率に従う必要があるからである。しかしこの制約を受けるが、可能な限り直線である。

測地線の性質は直線の性質とは異なる。例えば、平面上では平行線が交わることはないが地表上の測地線ではそうではない。例えば経線どうしは赤道において平行であるが極で交わる。同様に自由落下する試験粒子の世界線は時空測地線であり、時空において可能な限り直線である。しかし、これと特殊相対性理論の無重力次元で描かれる真の直線の間には大きな違いがある。特殊相対性理論においては、平行測地線は平行のままである。潮汐効果のある重力場では一般的にそうではない。例えば2つの物体が互いに相対的に静止しているがその後地球の重力場に落とされる場合、それらは地球の中心に向かって落ちるように互いに向かって移動する[17]。

惑星や他の天体と比較して、日常生活の物体（人、車、家、山でさえも）はほとんど質量を持たない。このような物体が関係する場合、試験粒子の振る舞いを支配する法則で何が起きるかを説明するのに十分である。特に、測地線の経路から試験粒子を逸らすためには外力を加える必要がある。誰かが座っている椅子は外向き上向きの力を加え、人が地球の中心に向かって自由落下し地球中心とそれらの間に物質がなければあったであろう測地線に従うことを妨げる。このようにして、一般相対性理論は地表上での重力の日常的な経験を、重力が下向きに引っ張るのではなく、外力が上向きに押すものとして説明する。これらの力は全ての物体が従ったであろう測地線から地表上にある全ての物体を逸らす[18]。自身の重力の影響を無視できない物質物体の場合、運動の法則は試験粒子の場合よりもやや複雑であるが、時空が物質に対してどのように動くかを伝えているのは事実である[19]。

重力源

[編集]

ニュートンによる重力の記述では、重力は物質により引き起こされる。より正確には、物質物体の特定の特性である質量により引き起こされる。アインシュタインの理論および関連の重力理論においては、時空のあらゆる点における曲率も存在する物質すべてにより引き起こされる。ここでも質量は物質の重力の影響を決定する重要な特性である。しかし、重力の相対論的理論においては、質量が唯一の重力源ではない。相対性理論は質量をエネルギーと、エネルギーを運動量と結び付ける。

E = mc2という式で表される質量とエネルギーの等価性は、特殊相対性理論の最も有名な結果である。相対性理論において、質量とエネルギーは1つの物理量を表す2つの異なる方法である。物理系がエネルギーを持つ場合、これに対応する質量もあり、逆も然りである。特に、核や分子などの系の温度や結合エネルギーなどエネルギーに関連する物体の全ての特性は、物体の質量に寄与し、すなわち重力源としてはたらく[20]。

特殊相対性理論において、エネルギーは運動量と密接に関連している。この理論では時空と同じように、時空、エネルギー、運動量と呼ばれるより包括的な実体の異なる面は、物理学者が4元運動量と呼ぶ統一された4次元量の異なる面にすぎない。その結果、エネルギーが重力源である場合、運動量も重力源でなければならない。同じことがエネルギーと運動量に直接関連する量、つまり内部圧力と張力にもあてはまる。以上をまとめると、一般相対性理論において質量、エネルギー、運動量、圧力、張力が重力源として働く。これらは時空にどのように曲がるかを伝える。理論の数学的定式化では、これらの量は全てエネルギー・運動量テンソルと呼ばれるより一般的な物理量のある面にすぎない[21]。

アインシュタイン方程式

[編集]

アインシュタイン方程式は一般相対性理論のセンターピースである。これにより、数学の言葉を用いた時空幾何学と物質の性質との関係の正確な定式化が提供される。もっと具体的には空間（もしくは時空）の幾何学的特性が、メトリックと呼ばれる量で記述されるリーマン幾何学の概念を用いて定式化される。メトリックは、曲空間（もしくは時空）における距離と角度の基本的な幾何学的概念を計算するために必要な情報をエンコードする。

経度30度の差に対応する、異なる緯度における距離

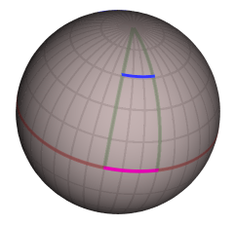
地表のような球面は簡単な例である。表面上の任意の点の位置は地理的な緯度と経度の2つの座標で記述される。右図に示すように、平面のデカルト座標とは異なり座標の違いは表面上の距離と同じではない。赤道にいる場合、西への経度30度の移動（マゼンタ色の線）はおよそ3,300キロメートル (2,100 mi)であるのに対し緯度55度にいる場合は西への経度30度の移動（青色の線）はわずか 1,900キロメートル (1,200 mi)である。したがって座標は球面の幾何学、実際にはもっと複雑な空間や時空の幾何学を記述するのに十分な情報を提供してくれない。その情報は正確にメトリックでエンコードされるものであり、このメトリックは表面（もしくは空間、時空）の各点で定義される関数であり、座標の差異を距離の差異に関連付ける。あらゆる与えられた曲線の長さや2つの曲線が交わる角度など、幾何学において重要なほかの全ての量は、このメトリック関数から計算できる[22]。

メトリック関数と点間の変化率を用いてリーマン曲率テンソルと呼ばれる幾何学的な量を定義できる。これは、各点で空間もしくは時空がどのように曲がるかを正確に記述する。一般相対性理論において、メトリックとリーマン曲率テンソルは時空の各点で定義された量である。すでに述べたように、時空の物質内容は別の量、エネルギー・運動量テンソル Tを定義し、「時空は物質にどのように動くかを伝え、物質は時空にどのように曲がるかを伝える」という原則はこれらの量が互いに関連しなければならないことを意味する。アインシュタインはリーマン曲率テンソルとメトリックを用いて現在アインシュタインテンソルと呼ばれ時空の曲がり方のいくつかの側面を記述する別の幾何学的量 G を定義することによりこの関係を定式化した。すると、アインシュタイン方程式は

となる。すなわち、定数倍まで量 G（曲率を測定する）は量 T（物質内容を測定する）と同等である。ここでGはニュートン重力の重力定数、cは特殊相対性理論による光速である。

量 G と T はそれぞれ時空の座標のいくつかの関数により決定されるため、この式は複数形Einstein's equationsと呼ばれることが多く、この式はこれらの成分関数と同等である[23]。これらの方程式の解は時空の特定の幾何学を記述する。例えば、シュワルツシルト解は恒星やブラックホールなど球体で非回転の質量の周りの幾何学を記述するが、カー解は回転するブラックホールを記述する。他の解によって重力波が記述され、フリードマン・ルメートル・ロバートソン・ウォーカー解の場合、膨張する宇宙を記述することができる。最も単純な解は曲がっていないミンコフスキー時空であり、特殊相対性理論により記述される[24]。

実験

[編集]

絶対に確実な科学理論はない。それぞれが実験により確認する必要があるモデルである。ニュートンの重力法則は太陽系内の惑星や月の運動をかなり正確に説明したため受け入れられた。実験的測定の精度が徐々に向上するにつれて、ニュートンの予測との間に矛盾がいくつか観測され、これらは一般相対性理論で説明された。同様に、一般相対性理論の予測も実験で確認する必要があり、アインシュタイン自身が理論の古典的試験として知られる3つの試験を考案した。

球状恒星を周回する1つの惑星のニュートンの軌道（赤）vs. アインシュタインの軌道（青）（アニメーション）
  • ニュートン重力は1つの惑星が完全に球体の恒星の周囲を回る軌道は楕円であるはずだと予測している。アインシュタインの理論はより複雑な曲線を予測している: 惑星が楕円の周りを移動しているように振舞うが、同時に楕円が全体として恒星の周りをゆっくり回転するというものである。右図では、ニュートン重力により予測された楕円が赤で示され、アインシュタインにより予測された軌道の一部が青で示されている。太陽の周りを回る惑星の場合、ニュートンの軌道からのこの逸脱は異常近日点移動として知られている。この効果の最初の測定は水星に対して行われ、1859年までさかのぼる。水星および他の惑星に対する最も正確な結果は電波望遠鏡を用いて1966年から1990年にかけて行われた測定に基づいている[25]。一般相対性理論は、これが正確に測定できる全ての惑星（水星、金星、地球）の正確な異常近日点移動を予測する。
  • 一般相対性理論によると、光は重力場を伝播するときに直線に沿って進まず、質量の大きい物体の存在下で曲げられる。特に星明かりは太陽の近くを通過する際に曲げられ、空の星の位置で見かけ上最大1.75秒角のずれが生じる（1秒角は1/3600度に等しい）。ニュートン重力の枠組みでは、その量の半分だけ光の曲がりにつながるヒューリスティックな議論を行うことができる。日食中に太陽に近い星を観測することで、様々な予測を試験することができる。この方法で、アーサー・エディントンが率いた1919年のイギリスの西アフリカ探検隊は1919年5月の日食の観測を通してアインシュタインの予測が正しいこと、ニュートンの予測が間違っていることを確認した。エディントンの結果はあまり正確ではなかった。その後、遠方のクエーサーの光の太陽による偏向の観測は、電波天文学の非常に正確な技術を利用してエディントンの結果をずっと良い精度で確認した（最初のこのような測定は1967年から、最近の包括的な分析は2004年から）[26]。
  • 重力赤方偏移は1959年PoundとRebkaにより実験室で最初に測定された。天体物理測定でも測定され、特に白色矮星シリウスBを避ける光に対して行われた。関連する重力による時間遅延効果は、原子時計を数十kmから数万kmの高度に輸送することで測定されている（最初は1971年にHafeleとKeatingにより、もっと正確なものは1976年に打ち上げられたGravity Probe Aにより）[27]。

これらの試験のうち、水星の近日点の前進のみが1916年のアインシュタインの一般相対性理論の最終発表以前に知られていた。アインシュタインの予測のその後の実験的確認、特に1919年の太陽による光のゆがみの最初の測定は、アインシュタインを国際的なスターダムにのし上げた[28]。これら3つの実験はニュートンの理論ではなく一般相対性理論を採用することを正当化し、付随的に提案されてきた一般相対性理論に対する多くの代替案を正当化した。 一般相対性理論のさらなる試験には、シャピロ効果や光の重力時間遅延の精密測定があり、最近では2002年にカッシーニ宇宙探査機により行われた。1セットの試験は宇宙を移動するジャイロスコープの動作に対する一般相対性理論により予測される効果に焦点を合わせている。これらの効果の1つ、測地歳差運動は、月レーザー測距実験（月の軌道の高精度測定）で試験されている。もう1つは回転する質量と関連しており、慣性系の引きずりと呼ばれている。測地効果と慣性系の引きずり効果は2004年に始まったGravity Probe B衛星実験で試験され、2008年12月の時点で相対性がそれぞれ0.5%と15%以内であることが確認されている[29]。

宇宙基準では、太陽系全体の重力は弱い。アインシュタインの理論とニュートンの理論の予測の差異は重力が強い場合に最も著しくなるため、物理学者は比較的強い重力場の環境で様々な相対論的効果を試験することに長らく興味を持っている。これは連星パルサーの精密な観測により可能になった。このような星系では、2つの非常にコンパクトな中性子星が互いに軌道を回っている。このうち少なくとも1つはパルサー（電波のタイトなビームを放射する天体）である。これらのビームは、灯台の回転ビームが観測者が灯台の点滅を見ることを意味するのと同じように、非常に規則的な間隔で地球にあたり、非常に規則的な一連のパルスとして観測することができる。一般相対性理論はこれら無線パルスの規則性からの特定の逸脱を予測する。例えば、電波が他の中性子星の近くを通過するときは時々この星の重力場により電波はゆがまされるはずである。観測されるパルスパターンは一般相対性理論により予測されるものに非常に近い[30]。

観測の特定のまとまりは、非常に有用で実用的な応用、すなわち、精密測位と計時の両方に使用されるGPSなどの衛星ナビゲーションシステムに関連している。このようなシステムは2組の原子時計、地球を周回する衛星に載せられた時計と、地表に設置された基準時計に依存している。一般相対性理論は、これらの2組の時計が異なる運動（特殊相対性理論により既に予測されている効果）と地球の重力場内の異なる位置によりわずかに異なる速度で進むはずだと予測する。システムの精度を保証するために、衛星の時計を相対論的要素により遅めるか、同じ要素を評価アルゴリズムの一部にする。同様に、システムの精度の試験（特に世界協定時の定義の一部である非常に徹底的な測定）は、相対論的予測の有効性を証明する[31]。

他の多くの試験が、等価原理の様々な解釈の妥当性を調べている。厳密にいえば重力時間膨張の全ての測定は一般相対性理論自体ではなく、等価原理の弱いものの試験である。現時点で一般相対性理論は全ての観測試験を合格している[32]。

天体物理学の応用

[編集]

一般相対性理論に基づくモデルは、天体物理学において重要な役割をしている。これらモデルの成功は、この理論の妥当性をさらに証明している。

重力レンズ

[編集]
アインシュタインの十字架: 重力レンズ（クエーサーよりはるか近くにある前景の銀河、Huchraのレンズ）により生成される同じ遠方にあるクエーサーの4つの像

光は重力場で曲げられるため、遠くの物体の光が複数の経路を通って観測者に到達することがある。例えば、クエーサーなど非常に遠方にある天体の光は、巨大な銀河の片側を通過し地球上の観測者に届くのにわずかに曲げられるが、同じ銀河の反対側を通過する光も曲げられてわずかに異なる方向から同じ観測者に届く。結果として、その観測者は1つの天体を2つの異なる場所で観測することになる。この種の焦点合わせは光学レンズに関してよく知られているため、この重力効果は重力レンズと呼ばれる[33]。

観測天文学では、このレンズ効果をレンズになる天体の特性を推測する重要な道具として用いる。その天体が直接見えない場合でも、レンズで曲げられた像の形は光のゆがみの原因となる質量分布に関する情報を提供してくれる。特に、重力レンズは光を放出せず重力効果によってのみ観測できる暗黒物質の分布を測定する1つの方法である。特に興味深い用途の1つが、観測可能な宇宙のかなりの部分にレンズとなる質量が広がっている大規模観測であり、我々の宇宙の大規模特性と進化に関する情報を取得するために使うことができる[34]。

重力波

[編集]

アインシュタインの理論の直接的な結果である重力波は、光の速度で伝播する幾何学のゆがみであり、時空の小さな波と考えることができる。流体力学における重力波とは異なる概念である。

2016年2月、Advanced LIGOのチームとVirgo干渉計チームがブラックホールの合体により生じた重力波を直接観測したと発表した[35]。

間接的には重力波の効果はある連星の観測により検出されていた。このような星のペアは互いに軌道を回っており、そうするにつれて重力波を放射し徐々にエネルギーを失う。太陽のような普通の恒星ではこのエネルギー損失は小さすぎて検出できないが、1974年PSR1913+16という連星パルサーで観測された。このような系では軌道を回る星の1つはパルサーである。これには2つの結果がある。パルサーは中性子星として知られる非常に密度の高い天体であり、重力波の放射は通常の星よりもずっと強い。また、パルサーは磁極から狭いビームの電磁放射線を放射する。パルサーが回転すると、灯台で回転する光からの規則正しい閃光を海上の船が観測するのと同じように、そのビームが地球上をスウィープし規則的に連なる無線パルスとして観測される。この無線パルスの規則的なパターンは非常に正確な「時計」として機能する。これは二重星の軌道周期を計るのに使うことができ、すぐ近くの時空のゆがみに鋭敏に反応する。It can be used to time the double star's orbital period, and it reacts sensitively to distortions of spacetime in its immediate neighborhood.

PSR1913+16の発見者であるラッセル・ハルスとジョゼフ・テイラーは1993年にノーベル物理学賞を受賞した。これ以降、他にもいくつかの連星パルサーが発見された。一般相対性理論の正確な試験を提供してくれることから、両方の星がパルサーであるものが最も役に立つ[36]。

現在、多くの地上配備の重力波検出器が稼動しており、宇宙配備の検出器を打ち上げるミッションであるLISAが現在開発中であり、その前身のミッション（LISA パスファインダー）が2015年に打ち上げられた。重力波の観測を用いて、中性子星やブラックホールなどのコンパクト天体に関する情報を取得したり、ビッグバンの1秒後の初期宇宙の部分の状態を調査したりすることができる[37]。

ブラックホール

[編集]
銀河M87の中心部から放出されるブラックホール駆動のジェット

質量が空間のコンパクト領域に十分集中する場合、一般相対性理論はブラックホールの形成を予測する。ブラックホールは重力の影響が非常に強く、光すら逃げられない空間領域のこと。ある種のブラックホールは、大質量星の進化の最終状態と考えられている。一方、太陽の数百万、数十億倍の質量を持つ超大質量ブラックホールはほとんどの銀河のコアに存在すると推測されており、過去数十億年にわたって銀河がどのように形成されたかという現在のモデルで重要な役目をしている[38]。

コンパクト天体に落ちていく物質は、放射の形でエネルギーを放出するための最も効率的なメカニズムの1つであり、ブラックホールに落ちていく物質は考えうる最も明るい天文現象のいくらかの原因であると考えられている。天文学者にとって非常に興味深い注目すべき例は、クエーサーや他のタイプの活動銀河核である。適切な条件下では、ブラックホールの周りに蓄積する落下物質はジェットの形成につながるかもしれない。ジェットでは物質の集束ビームが光速に近い速度で宇宙に投げ出される[39]。

ブラックホールの特性には最も有望な重力波源である理由となるものがいくつかある。理由の1つは、ブラックホールは連星系の一部として互いに周回できる最もコンパクトな天体であることである。結果的にこのような系により放出される重力波は特に強い。もう1つの理由はブラックホール唯一性定理（時間の経過とともにブラックホールは最初の幾何学的形状に関係なく特徴の最小限のセットを保持する（これらの定理は無毛定理として知られる））からなる。例えば、長期的には、仮想的な物質立方体が崩壊しても立方体の形のブラックホールは発生しない。その代わり結果として生じたブラックホールは球状の質量の崩壊により形成したブラックホールと区別することができない。球状への変化では、より複雑な形の崩壊により形成されたブラックホールは重力波を放出する[40]。

宇宙論

[編集]

一般相対性理論の最も重要な面の1つは、宇宙全体に適用できることである。重要な点は、大規模ではわれわれの宇宙は非常に単純な線に沿って構築されているように見えることである。現在の全ての観測では観測者の位置や観測方向に関係なく平均して宇宙の構造はほぼ同じであるべきである。宇宙は一様等方である。このような比較的単純な宇宙は、アインシュタイン方程式の単純解により説明できる。現在の宇宙の宇宙論的モデルは、一般相対性理論に対するこれら単純の解と宇宙の物質内容の特性、すなわち熱力学、核物理学、素粒子物理学を記述する理論と組み合わせることにより得られる。これらのモデルによると、われわれの現在の宇宙は約140億年前に非常に高密度な高温状態（ビッグバン）から出現し、それ以降膨張している[41]。

アインシュタイン方程式は宇宙定数と呼ばれる項を追加することにより一般化できる。この項が存在する場合、空の空間自体が引きあう（もしくはあまり一般的ではないが斥けあう）重力源として働く。アインシュタインは元々この項を先駆的な1917年の論文で最初に導入したが、非常にはっきりとした動機があった: 当時の宇宙論的考えでは宇宙を静的であるとみなしており、一般相対性理論の枠組みの中で静的なモデル宇宙を構築するために追加の項が必要であった。宇宙が静的ではなく膨張していることが明らかとなったとき、アインシュタインはすぐにこの追加項を破棄した。しかし、1990年代終わり以降宇宙定数（もしくは同様に特別で遍在するダークエネルギーの類い）と一致する加速膨張を示す天文学的証拠が着実に蓄積されてきている[42]。

現代の研究

[編集]

一般相対性理論は、印象的な一連の物理現象を記述する正確なモデルの枠組みを与えることに非常に成功している。その一方、多くの興味深い未解決の問題があり、特に理論全体としてはほぼ間違いなく不完全である[43]。

基本相互作用の他の全ての現代理論とは対照的に、一般相対性理論は古典理論である。これには量子物理学の効果が含まれない。一般相対性理論の量子版の探究は物理学の最も基本的な未解決問題の1つにあたる。量子重力理論として特に弦理論やループ量子重力理論など有望な候補はあるが、現時点では一貫して完全な理論は無い。長らく量子重力理論が一般相対性理論の別の問題のある特徴、時空特異点の存在を排除することが望まれている。これらの特異点は、幾何学がうまく定義できない時空の境界（「鋭い刃」）であり、一般相対性理論自体が予測力を失う。さらに、一般相対性理論の法則が量子修正なしで成り立つ場合、そのような特異点が宇宙内にそんざいしなければならないと予測するいわゆる特異点定理がある。最も有名な例はブラックホールと宇宙の始まりを記述するモデル宇宙に関連する特異点である[44]。

一般相対性理論を修正する他の試みは宇宙論の文脈で行われた。現代宇宙論のモデルでは、宇宙のほとんどのエネルギーは直接検出できていない形、すなわちダークエネルギーと暗黒物質の形で存在している。例えば修正ニュートン力学など重力と宇宙膨張の力学を支配する法則を修正することにより、これらの謎の形をした物質とエネルギーの必要性を取り除こうとした論争になっている提案がいくつかある[45]。

量子効果や宇宙論の挑戦を越えて、一般相対性理論の研究はさらなる探究の可能性に富んでいる。数学的相対主義者は、特異点の性質とアインシュタイン方程式の基本的性質を探究し[46]、特殊な時空のより包括的なコンピュータシミュレーション（ブラックホールの合体を記述するものなど）を実行している[47]。理論が最初に発表されてから100年以上が経過し、研究はこれまで以上に活発になっている[48]。

関連項目

[編集]
ポータル 物理学
ポータル 物理学
ポータル 天文学
ポータル 天文学

脚注

[編集]
  1. ^ この発展は例えばRenn 2005, p. 110ff.、Pais 1982の9章から15章、Janssen 2005で追うことができる。ニュートン重力を要約したものはSchutz 2003, chapters 2–4にある。ニュートン重力の問題が1907年以前にアインシュタインの頭をよぎったかどうかは不明だが、自らの認めるところではその理論を特殊相対性理論と調和させようという最初の真剣な取り組みは1907年からである。cf. Pais 1982, p. 178.
  2. ^ 詳しくはWheeler 1990第2章参照
  3. ^ 等価原理は今でも一般相対性理論の現代的な説明の一部であるが、現在のものとアインシュタインの元々の概念の間には違いがいくつかある。cf. Norton 1985.
  4. ^ 例えばJanssen 2005, p. 64f。アインシュタイン自身も非技術的な本Einstein 1961の第20節でこれを説明している。エルンスト・マッハによる以前のアイデアに従い、遠心力や他の重力に類するものも調査した。cf. Stachel 1989.
  5. ^ アインシュタインはこれをEinstein 1961の第20節で説明した。彼は加速するロケットに乗せられた部屋の天井からロープで「吊り下げられた」物体を考えた。部屋の中からだとそれは重力が物体をその質量に比例した力で引き下げているように見えるが、ロケットの外からだとロープが単にロケットの加速度を物体に伝達しているように見えるため、そのために「力」のみを及ぼす必要がある。
  6. ^ より具体的には、Pais 1982の11b章で説明されているアインシュタインの計算は等価原理、重力と慣性力の等価性、光の伝播と加速された観測者の特殊相対性理論の結果（後者は各瞬間にそのような加速された観測者に関連する瞬間の慣性基準系を考えることにより）を用いる。
  7. ^ この効果は、加速されたロケット船にいる2人の観測者の同等の状態を見るか、落下するエレベーターを見ることにより特殊相対性理論の範囲内で直接導き出すことができる。どちらの状況でも周波数シフトは、特定の慣性系の間のドップラーシフトと同等の説明を持つ。これの簡単な導出についてはHarrison 2002参照
  8. ^ Mermin 2005の12章参照
  9. ^ Cf. Ehlers & Rindler 1997; for a non-technical presentation, see Pössel 2007.
  10. ^ これや他の潮汐効果についてはWheeler 1990, pp. 83–91で説明されている。
  11. ^ 潮やその幾何学的解釈はWheeler 1990の5章で説明されている。歴史的発展のこの部分はPais 1982, section 12bで追うことができる。
  12. ^ 時空の概念の初歩的な説明についてはThorne 1994の2章の最初の節と、Greene 2004, p. 47–61参照。かなり初歩的なレベルでのより完全な論は、例えばMermin 2005やWheeler 1990, chapters 8 and 9で見ることができる。
  13. ^ Marolf, Donald (1999). “Spacetime Embedding Diagrams for Black Holes”. General Relativity and Gravitation 31: 919–944. arXiv:gr-qc/9806123. Bibcode: 1999GReGr..31..919M. doi:10.1023/A:1026646507201. 
  14. ^ 曲がった時空のはっきりした図はWheeler 1990, chapters 8 and 9参照。
  15. ^ アインシュタインの正しい場の方程式を見つけ出す苦闘はPais 1982の13-15章で辿ることができる。
  16. ^ 例えばWheeler 1990のp. xi
  17. ^ 基本的な微分幾何学とその応用の完全であり分かりやすい説明はGeroch 1978で見ることができる。
  18. ^ Wheeler 1990の第10章参照。
  19. ^ 実際、完全な理論から始めるとアインシュタインの方程式を用いて幾何学の結果として物質のより複雑な運動法則を導くことができるが、ここから理想化した試験粒子の運動を導き出すのは非常に重要な作業である。cf. Poisson 2004
  20. ^ 質量-エネルギー透過性の簡単な説明はGiulini 2005の3.8と3.9節にある。
  21. ^ Wheeler 1990の第6章参照。
  22. ^ メトリックのより詳しい定義であるが、教科書の説明よりもくだけた定義についてはPenrose 2004の14.4章参照。
  23. ^ アインシュタイン方程式の幾何学的意味はWheeler 1990の第7,8章で探究されている。cf. Thorne 1994のbox 2.6。非常に単純な数学のみを用いた導入はSchutz 2003の第19章に記されている。
  24. ^ 最も重要な解は全ての一般相対性理論の教科書にリストアップされている。現在の理解の（技術的な）まとめはFriedrich 2005参照。
  25. ^ より正確には、これらは惑星の位置のVLBI測定である。Will 1993の第5章およびWill 2006の3.5節参照。
  26. ^ 歴史的な測定についてはHartl 2005、Kennefick 2005、Kennefick 2007参照。ニュートンの理論のフレームワークにおけるSoldnerの最初の導出はvon Soldner 1804にある。これまでで最も正確な測定についてはBertotti 2005参照。
  27. ^ Kennefick 2005とWill 1993の第3章参照。シリウスBの測定については、Trimble & Barstow 2007参照。
  28. ^ Pais 1982, Mercury on pp. 253–254, アインシュタインの名声の向上は16bと16c節にある。
  29. ^ Everitt, C.W.F.; Parkinson, B.W. (2009) (PDF), Gravity Probe B Science Results—NASA Final Report, http://einstein.stanford.edu/content/final_report/GPB_Final_NASA_Report-020509-web.pdf 2009年5月2日閲覧。 
  30. ^ Kramer 2004.
  31. ^ GPSにおける相対論的効果の分かりやすい説明はAshby 2002で見られる。詳しくはAshby 2003にある。
  32. ^ 一般相対性理論の試験への分かりやすい導出はWill 1993にある。より技術的、最新の説明はWill 2006にある。
  33. ^ このような状況の幾何学はSchutz 2003の第23章で探究されている。
  34. ^ 重力レンズとその応用についての導入は、ウェブページNewbury 1997とLochner 2007にある。
  35. ^ B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016). “Observation of Gravitational Waves from a Binary Black Hole Merger”. Physical Review Letters 116 (6): 061102. arXiv:1602.03837. Bibcode: 2016PhRvL.116f1102A. doi:10.1103/PhysRevLett.116.061102. PMID 26918975. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.116.061102. 
  36. ^ Schutz 2003, pp. 317–321; Bartusiak 2000, pp. 70–86.
  37. ^ 重力波の現在進行中の調査はBartusiak 2000とBlair & McNamara 1997に書かれている。
  38. ^ 20世紀初頭から現代までのブラックホール物理学の歴史の概要については、Thorne 1994による非常に読みやすい説明参照。構造形成におけるブラックホールの役割についての最新の説明についてはSpringel et al. 2005参照。簡単なまとめは関連記事Gnedin 2005にある。
  39. ^ Sparke & Gallagher 2007の第8章とDisney 1998参照。より完全で比較的数学が少ない論はRobson 1996で見られる。
  40. ^ ブラックホールの唯一性定理の基本的な導入はChrusciel 2006とThorne 1994, pp. 272–286で見られる。
  41. ^ 詳細な情報はNed WrightのCosmology Tutorial and FAQ, Wright 2007にある。非常に読みやすい導入はHogan 1999にある。Berry 1989では学部レベルの数学を用いるが高度な数学を避けて一般相対性理論の完全な紹介をしている。
  42. ^ アインシュタインの原著論文はEinstein 1917である。現代的な発展の良い記述はCowen 2001とCaldwell 2004にある。
  43. ^ Cf. Maddox 1998, pp. 52–59と98–122; Penrose 2004, section 34.1とchapter 30.
  44. ^ 弦理論に焦点を合わせた量子重力の研究はGreene 1999にある。ループ量子重力の観点からの説明についてはSmolin 2001参照。
  45. ^ 暗黒物質についてはMilgrom 2002参照。ダークエネルギーについてはCaldwell 2004参照。
  46. ^ Friedrich 2005参照。
  47. ^ 様々な問題とそれを解決するために開発されている技術のレビューについては、Lehner 2002参照。
  48. ^ 相対性理論の現在の研究のスナップショット（概観）の出発点としては、電子工学のレビュージャーナルLiving Reviews in Relativityが良い。

参考文献

[編集]

外部リンク

[編集]

Additional resources, including more advanced material, can be found in General relativity resources.