Asymmetrische inductie

Met asymmetrische inductie, ook wel enantio-inductie genoemd, wordt in de stereochemie het effect beschreven waarbij de ruimtelijke structuur van een molecuul bij de vorming van nieuwe bindingen in het molecuul effect heeft op de ruimtelijke oriëntatie van die nieuwe bindingen. Zonder asymmetrische inductie zal bij een nieuw chiraal centrum in een molecuul, de productverhouding tussen beide mogelijkheden 1:1 zijn. Asymmetrische inductie zorgt ervoor dat (door de aanwezigheid van een chiraal centrum in het molecuul) een van de twee mogelijke producten meer (en bij voorkeur uitsluitend) gevormd wordt. De oorspronkelijke chiraliteit kan zowel in het substraat, een van de reagentia of een gebruikte katalysator voorkomen.^[1] Asymmetrische inductie speelt een sleutelrol in de asymmetrische synthese.

Zowel het begrip als de eerste toepassingen ervan zijn geïntroduceerd door Emil Fischer tijdens zijn werk aan koolhydraten.^[2] Inmiddels zijn verschillende typen van asymmetrische inductie beschreven:

• Interne asymmetrische inductie maakt gebruik van een ander chiraal centrum dat covalent met het reactiecentrum is verbonden, en dat ook blijft tijdens het verloop van de reactie. Het uitgangsmateriaal is doorgaans afkomstig uit een chirale synthesepool.
• In gekoppelde asymmetrische inductie wordt de chirale informatie eerst geïntroduceerd tijdens een afzonderlijke reactiestap. Na de reactie waarbij de inductie optreedt, wordt de sturende groep weer verwijderd. Het gebruikte asymmetrische synthon wordt aangeduid als chirale hulpstof.
• In het geval van externe asymmetrische inductie wordt de chirale informatie doorgegeven in de overgangstoestand met behulp van een chirale katalysator.

De laatste vorm van asymmetrische inductie is vanuit het standpunt van enantiomere economie het meest voordelig.

De carbonylgroep: 1,2-inductie

De carbonylgroep vormt in de organische chemie een belangrijke synthetische draaischijf: er is zowel een groot aantal reacties bekend om de groep te synthetiseren als reacties waarbij andere functionaliteiten de plaats van de carbonylgroep innemen. De manier waarop asymmetrische inductie rond deze groep gerealiseerd kan worden is dan ook uitvoerig bestudeerd, evenals de achterliggende redenen van de gevonden selectiviteit. Deze studies hebben in een aantal modellen geresulteerd, die sterische en elektronische achtergronden in hun beschouwingen meenemen, maar nog lang niet altijd met elkaar in overeenstemming zijn. De belangrijkste van deze modellen zijn die van Cram (1952), Cornforth (1954) en Felkin (1956).

Regel van Cram

De regel van Cram met betrekking tot asymmetrische inductie is in 1952 geformuleerd door Donald J. Cram. ^[3] De regel is een vroege poging tot het voorspellen van de stereochemische uitkomst van een synthese in een acyclisch systeem. Cram omschreef de regel aldus:

In bepaalde niet-gekatalyseerde reacties zal dat diastereomeer het meest gevormd worden, waarin de nadering van de inkomende groep plaatsvindt langs de minst gehinderde zijde zodanig dat de carbonylgroep zich in de rotatie-conformatie van de koolstof-koolstofbinding bevindt tussen de twee ruimtelijk gezien kleinste groepen aan het naastliggende asymmetrische centrum.^[4]

De regel geeft aan dat indien een molecuul een chiraal centrum bevat, bij de vorming van een tweede chiraal centrum de sturing wordt uitgeoefend via sterische hindering.

In 1952 publiceerde Cram een groot aantal reacties waarbij de voorkeurconformatie (zelden wordt een volledige inductie verkregen) van de producten beschreven kon worden via deze benadering. Onderstaand reactieschema geeft een van de door Cram gebruikte voorbeelden weer.

Schema 1. Asymmetrische inductie en de Regel van Cram

In het experiment werden 2 reacties gebruikt. In de eerste reactie werd aan 2-fenylpropanal (1)^[5] fenylmagnesiumbromide, het Grignard-reagens van broombenzeen toegevoegd waarbij 1,2-difenyl-1-propanol (2) ontstaat als een mengsel van diastereomeren, zij het voornamelijk de threo-isomeer.

De vorming van het threo-isomeer kan met behulp van de regel worden uitgelegd (zie ook de newmanprojectie A). Het nucleofiel nadert de carbonylgroep vanaf de minst gehinderde zijde, waarbij de carbonylgroep in een staggered positie staat ten opzichte van de methylgroep en het waterstofatoom, de twee kleinste substituenten, waardoor de sterische hindering tot een minimum wordt beperkt en de grote fenylgroep in de anti-conformatie.

De tweede reactie is de reductie van 1,2-difenylpropanal 2 met lithiumaluminiumhydride, waarbij dezelfde reactieproducten als in de vorige reactie ontstaan, maar nu met het erythro-isomeer als voornaamste component (2a). Ook nu wordt de carbonylgroep door het nucleofiel, het hydrideanion H⁻, benaderd vanaf de minst gehinderde positie. In de afbeelding komt het waterstof vanachter naar de getekende structuur toe.

In de tijd van de originele publicatie was spectroscopische identificatie van de producten nog niet goed mogelijk en werd het structuurbewijs voor de twee reactieproducten geleverd door ze te onderwerpen aan een Chugaev-eliminatie, waarbij het threo-isomeer omgezet wordt in Z-α-methyl-stilbeen en de erythro-verbinding aanleiding geeft tot het E-isomeer.

Schema 2. Chugaev-eliminatie na asymmetrische inductie (Cram)

Model van Felkin

Het Felkin-model uit 1968, genoemd naar Hugh Felkin, voorspelt ook de stereochemie tijdens de nucleofiele additie aan de carbonylgroep.^[6] Felkin betoogde dat het model van Cram een belangrijk nadeel heeft: in de overgangstoestand is een eclipsed conformatie noodzakelijk tussen de substituent (het waterstofatoom van het aldehyde) en de grootste substituent op het α-koolstofatoom. Felkin liet zien dat door de substituent op het carbonylkoolstofatoom van waterstof via methyl, ethyl, isopropyl en isobutyl te vergroten, de stereoselectiviteit van de reactie ook groter wordt. Crams model kan dit effect niet voorspellen:

	Schema 3: Het Felkin model voor de asymmetrische inductie
	R	erythro / threo
	Me	74/26
	Et	76/24
	i-Pr	83/17
	t-Bu	98/2

De regels van Felkin laten zich als volgt samenvatten:

• De overgangstoestand lijkt sterk op de reactanten.
• Spanning in bindingen, ook in partiële bindingen, vormen een substantieel deel van de totale energie-inhoud van de overgangstoestand, zelfs als de binding nog maar voor een klein deel gevormd is. De conformatie is staggered en niet eclipsed met de substituent R op het carbonylkoolstofatoom naast de kleinste groep op het chirale koolstafatoom. Zie de conformatie "A" in de figuur hieronder.

Schema 4: De overgangstoestand volgens Felkin (A) vergeleken met die volgens Cram (B).

• De voornaamste sterische interactie hangt samen met de groep R en het nucleofiel, het zuurstofatoom doet hierin niet mee.
• Groepen die via polarisatie- of elektronische effecten een overgangstoestand kunnen stabiliseren zullen een zo groot mogelijke afstand hebben tot het reactiecentrum.

Activering zal betekenen dat er lading aan het reactiecentrum onttrokken wordt door een elektronegatieve groep, maar die lading moet "ergens" in het molecuul blijven. Hoe verder de negatieve lading bij het reactiecentrum vandaan zit, hoe minder afstotende werking ervan uit zal gaan naar het inkomende nucleofiel. Zo verlopen reacties met haloketonen niet volgens de regel volgens Cram. Ook in bovenstaand voorbeeld heeft het vervangen van de elektronegatieve fenylring door een cyclohexylgroep een negatief effect op de stereoselectiviteit.

Het Felkin-Anh model

Het Felkin-Anh model^[7] is een uitbreiding van het Felkin-model door Nguyen T. Anh en O. Eisenstein waarmee twee zwakkere punten in het model van Felkin gecorrigeerd worden:

• Het eerste punt betrof Felkins uitspraak met betrekking tot een sterk polarisatie-effect in de nucleofiele additiereacties, waarbij een S_N2-reactie tot een complete inversie van de stereochemie leidt zonder daar een goede uitleg voor te geven. Anh gaf aan dat in de antiperiplenaire overgangstoestand zowel sterische effecten ten gevolge van substituenten als orbitaaleffecten een rol spelen bij de asymmetrische inductie.^[8][9] Op deze manier ontstaat de beste parallelle oriëntatie tussen de nucleofiele σ* orbitaal en de π en π* orbitalen van de carbonylgroep, het inkomende anion wordt hierdoor optimaal gestabiliseerd.

	Schema 5: Polair effect volgens Felkin tegenover het anti-periplanair effect volgens Ahn.
	Nu	=	Nucleofiel
	R	=	Substituent op het carbonylkoolstofatoom, in de rechter tekening is dat het waterstofatoom.
	RM	=	Wat sterische eisen of grootte betreft de middelste substituent
	RM/L	=	In het model van Ahn is de grootte van de substituent niet belangrijk, het kan zowel de grootste of de op een na grootstre substituent zijn.
	RS	=	Kleinste substituent
	X	=	Elektronenzuigende substituent

• Een tweede probleem werd gevorm door de minimalisatie van substituent-interactie, wat niet opgaat voor aldehyden.

Schema 6: Zonder echte tweede substituent op het carbonylkoolstofatoom, zoals bij aldehyden het geval is, treedt ook geen sterische hindering of interactie op. RM zal volgens het model bij voorkeur bij het waterstofatoom in plaats van het zuurstofatoom zitten, waardoor de verkeerde geomettrie voor de route van het inkomende nucleofiel voorspeld wordt.

Toepassen van het Bürgi-Dunitz-traject^[10][11] stelde Nguyen in staat een niet-loodrechte route voor het nucleofiel aan te nemen: elke hoek tussen 95° en 105° ten opzichte van de zuurstof-koolstofbinding werd mogelijk, waardoor de voorspelbaarheid van de reactie rond aldehyden (het reactiepad loopt dichter langs het waterstofatoom) werd opgelost.^[8][12][13]

	Schema 7: Niet-loodrechte nadering van het nucleofiel volgens Ahn. Links de optimale benadering van het nucleofiel langs de kleinste substituent op het chirale centrum, rechts de meer gehinderde nadering langs de minder gunstige route. De grootste substituent bevindt zich steeds naar onderen gericht.
	Nu:	=	Nucleofiel
	RL	=	Wat sterische eisen of grootte betreft de grootste substutuent.
	RM	=	Wat grootte betreft de middelste substituent
	RS	=	Wat grootte betreft de kleinste substituent

Anti–Felkin selectiviteit

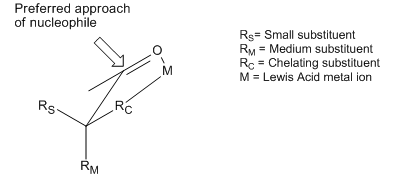
Hoewel het Cram-model enerzijds en dat van Felkin en Anh anderzijds verschillen in aannames en gebruikte conformeren, trachten beide hetzelfde fenomeen te beschrijven en te verklaren: de additie van een nucleofiel aan de sterisch meest gunstige zijde van een carbonylgroep. Er bestaat echter ook een groot aantal reacties dat zich tegenovergesteld gedraagt aan wat de regels van zowel Cram als Felkin–Anh voorspellen. Hoewel voor beide modellen pogingen ondernomen zijn deze afwijkingen te verklaren en daarmee deze vreemde reacties binnen het bereik van de verschillende modellen te brengen, staan ze nog steeds bekend als "anti-Felkin" reacties. Substitutie van het α-koolstofatoom met een groep die eigenschappen van een lewisbase bezit, optredend in O, N, S, of P substituenten, leidt tot anti-Felkin-gedrag. Als in deze situatie een lewiszuur zoals Al-iPr₂ of Zn²⁺ in het molecuul wordt ingebouwd ontstaat door intramoleculaire complexvorming tussen het metaal en de carbonylgroep een bidentaat ligand. In deze situatie wordt de carbonylgroep in een eclipsed conformatie geforceerd, waardoor het inkomende nucleofiel langs de kleinste substituent op het α-koolstofatoom nadert.^[14] Als de complexerende groep als grootste groep wordt aangewezen, zal dit leiden tot een "anti-Felkin"-product.

	Schema 8: Configuratie als complexatie aan de carbonylgroep optreedt. Het nucleofiel nadert langs een traject waar de kleinste en de grootste substituent pal naast liggen, di tin tegenstalling tot de oorspronkelijke aannames op dit gebied: het product wordt anti-Felkin
	Nu:	=	Nucleofiel
	RC	=	Substutuent met de complexerende groep erin. Dit zal doorgaans sterisch de grootste substituent
	RM	=	Wat sterische eisen of grootte betreft de grootste substutuent.
	RS	=	Wat grootte betreft de middelste substituent

Ook Cram onderkende het effect van de complexvorming, en voegde aan zijn set regels de voorwaarde toe dat ze slechts golden voor situaties waarin complexvorming geen rol speelt.^[15] Een voorbeeld van een dergelijke, onder andere via complexatie gestuurde reactie waarbij ook het complex werd aangetoond is in 1987 beschreven. Dergelijke complexen worden als Cram-chelaat aangeduid.^[16]

Schema 9: Asymmetrische inductie waarbij complexvorming een rol speelt. In dit geval kan het Cram-complex aangetoond worden.

In dit voorbeeld vormt methyltitanium(IV)chloride het Cram-chelaat. Na de vorming van het complex dissocieert de methylgroep en reageert deze op een anti-Felkin manier met de carbonylgroep.

Een niet-complexerende elektronenzuigende groep kan ook aanleiding geven tot een anti-Felkin-selectiviteit. Als de substituent elektronegatief genoeg is zal het nucleofiel "anti" adderen, zelfs als de elektronenzuigende groep niet de grootste groep aan het α-koolstofatoom is. Elk van de modellen geeft een iets andere verklaring voor het verschijnsel. Het polaire effect dat hier speelt werd zowel door Cornforth gepostuleerd^[17] als in het originele Felkin-model genoemd:^[18] beiden plaatsen de elektronzuigende groep en het inkomende nucleofiel anti- ten opzichte van elkaar. Het effect is dat het totale dipoolmoment in de overgangstoestand geminimaliseerd wordt.

	Schema 10: newmanprojectie van de configuratie waarin een polair effect optreedt, wat aanleiding geeft tot een anti-Felkin-product
	EWG	=	Elektronenzuigende groep (Electron Withdrawing Group). Deze groep neemt, onafhankelijk van zijn werkelijke grootte, de positie van grootste groep in: anti ten opzichte van het inkomende nucleofiel.
	Nu^−	=	Nucleofiel
	R	=	Tweede substituent aan het carbonylkoolstofatoom
	RL	=	Grootste substituent aan het chirale koolstofatoom
	RS	=	Kleinste substituent aan het chirale koolstofatoom

Het verbeterde Felkin-Anh-model, zoals het hierboven is weergegeven, maakt gebruik van moleculaire orbitalen om de stabilisatie te beschrijven in de voorkeursconformatie van de overgangstoestand. Een typisch voorbeeld van een reactie die met behulp van dit model beschreven wordt, is hieronder weergegeven:

Schema 11: Anti-Felkin-reactie

De carbonylgroep: 1,3-inductie

Naast de 1,2-inductie is ook 1,3-inductie waargenomen bij addities aan de carbonylgroep. In de loop der jaren is een aantal modellen ontwikkeld om de asymmetrische inductie via het β-koolstofatoom te beschrijven.

Complexvorming

Volgens Reetz, kan het Cram-complexvormingsmodel voor de 1,2-inductie uitgebreid worden naar β-alkoxyaldehyde-complexen rond metalen. Het nucleofiel nadert via de sterisch minst gehinderde zijde en anti- ten opzichte van de R_β-subsituent, wat aanleiding geeft tot het anti-adduct als het voornaamste product.^[19]

Om dit soort complexen te vormen dient het metaal te beschikken over minstens twee vrije coördinatieplaatsen en de sturing kan alleen optreden als er een lewisbase aanwezig is op de β-positie in de carbonylverbinding.

Zonder complexvorming

Model van Cram en Reetz (1984)

Cram en Reetz hebben aangetoond dat 1,3-asymmetrische inductie mogelijk is via een acyclische overgangstoestand. De reactie van β-alkoxy-aldehyden met allyltrimethylsilaan leidde in goede opbrengsten tot de anti-1,3-diolen, wat goed verklaard kan worden met behulp van het polaire Cram model. De polaire benzyloxy-groep staat anti ten opzichte van de carbonylgroep, waarbij dipoolinteracties tot een minimum beperkt worden en het nucleofiel via de anti-zijde ten opzichte van de grotere (R_M)groep binnekomt.^[20]

Model van Evans (1994)

Tien jaar later werd door Evans ander model geïntroduceerd voor de 1,3-inductie. In dit model is het β-stereocentrum anti- geplaatst ten opzichte van het inkomende nucleofiel, net als in het Felkin-Anh-model. De polaire groep "X" op het β-koolstofatoom staat anti- ten opzichte van de carbonylgroep waardoor de dipoolinteractie geminimaliseerd wordt, de substituent Rβ staat anti- ten opzichte van de aldehydegroep zodat ook sterische hindering zo klein mogelijk is. Als een gevolg wordt het 1,3-anti-diol voorspeld als voornaamste product.^[21]

Dubbele inductie: zowel 1,2- als 1,3-inductie

Als zowel het α- als het β-koolstofatoom asymmetrisch zijn dienen zowel de Felkin-Anh-regels (1,2-inductie) als de regels uit het Evans model (1,3-inductie) te worden toegepast. Indien de twee stereocentra onderling een anti-oriëntatie hebben, voorspellen beide modellen hetzelfde diastereomeer:

Is de relatie tussen beide chirale centra syn dan voorspellen de twee sets een verschillende uitkomst. Ervaringswijsheid is dat de grootte van het inkomende nucleofiel doorslaggevend is voor de regel die gevolgd wordt:

• Indien het nucleofiel groot is, wordt de interactie met het α-stereocentrum bepalend en vormt het Felkin-Ahn-product het grootste deel van de opbrengst.
• Een kleiner nucleofiel heeft tot gevolg dat de 1,3-interactie domineert, en het Evans-isomeer als hoofdproduct optreedt.^[22]

Externe link

• The Evolution of Models for Carbonyl Addition Evans Group Afternoon Seminar Sarah Siska February 9, 2001

Bronnen, noten en/of referenties

1. . definitie Gold Book – IUPAC Internetpagina: definitie . Gearchiveerd op 10 juni 2007.
2. Ari Koskinen. GEEN TITEL OPGEGEVEN Asymmetric Synthesis of Natural Products – ISBN 0-471-93848-3
3. Donald J. Cram, Fathy Ahmed Abd Elhafez. (1952). Studies in Stereochemistry. X. The Rule of "Steric Control of Asymmetric Induction" in the Syntheses of Acyclic Systems J. Amer. Chem. Soc.. 74 (23): pag.: 5828–5835 Internetpagina: Uittreksel . Gearchiveerd op 30 oktober 2008.
4. In de oorspronkelijke versie luidt de regel: In certain non-catalytic reactions that diastereomer will predominate, which could be formed by the approach of the entering group from the least hindered side when the rotational conformation of the C-C bond is such that the double bond is flanked by the two least bulky groups attached to the adjacent asymmetric center.
5. In het schema is het R-enantiomeer weergegeven, in het experiment werd een racemaat gebruikt. Omdat, onafhankelijk van het reagerende enantiomeer, reactie via de sterisch minst gehinderde zijde het threo-isomeer ontstaat, is het voor de bewijsvoering niet belangrijk dat geen stereochemisch zuivere verbinding gebruikt werd.
6. Marc Chérest, Hugh Felkin, Nicole Prudent. (1968). Torsional strain involving partial bonds. The stereochemistry of the lithium aluminium hydride reduction of some simple open-chain ketones Tetrahedron Lett.. 9 (18): pag.: 2199–2204 DOI:10.1016/S0040-4039(00)89719-1
7. Naast Felkin wordt hier als tweede auteur "Ahn" genoemd. In het Vietnamees is het gebruikelijk de familienaam eerst te noemen. Uitbreiding van de Felkinregel door Nguyen T. Anh zou eigenlijk moeten leiden tot het Felkin-Nguyen model.
8. Nguyen T.A. , O. Eisenstein. (1977). GEEN TITEL OPGEGEVEN Nouv. J. Chim.. 1977 (1): pag.: 61
9. Nguyen T.A., O. Eisenstein, J-M. Lefour, M-E. Dau. (1973). GEEN TITEL OPGEGEVEN J.Amer.Chem.Soc. 95 Collective volume 6146
10. H.B. Bürgi, J.D. Dunitz, E. Shefter. (1973). GEEN TITEL OPGEGEVEN J.Amer.Chem.Soc.. 95 pag.: 5065
11. H.B. Bürgi, J.D. Dunitz, J.M. Lehn, G. Wipff. (1974). GEEN TITEL OPGEGEVEN Tetrahedron. 30 pag.: 1563
12. Nguyen T.A. ; O. Eisenstein. (1976). GEEN TITEL OPGEGEVEN Tetrahedron Lett.. 1976 pag.: 155
13. Nguyen T. Ahn. (1980). GEEN TITEL OPGEGEVEN Top. Curr. Chem.. 88 pag.: 146
14. A. Mengel, O. Reiser. GEEN TITEL OPGEGEVEN Chem.Rev. 99 (5): pag.: 1191–1224
15. D.J. Cram, F.A. Elhafez. (1952). GEEN TITEL OPGEGEVEN J.Amer.Chem.Soc. 74 (23): pag.: 5835 Collective volume 5828
16. M.T. Reetz, M. Hullmann, T. Seitz. (1987). GEEN TITEL OPGEGEVEN Angew.Chem.Int.Ed.. 26 pag.: 477–480
17. J.W. Cornforth, M.R.H. Cornforth, K.K. Mathew. (1959). GEEN TITEL OPGEGEVEN J.Chem.Soc. 1959 pag.: 112–127
18. M. Cherest, H. Felkin, N. Prudent. (1968). GEEN TITEL OPGEGEVEN Tetrahedron Lett.. 18 pag.: 2199–2204
19. M.T. Reetz, A. Jung. (1983). GEEN TITEL OPGEGEVEN j.Amer.Chem.Soc.. 105 pag.: 4833
20. Zie:
    • T.J. Leitereg, D.J. Cram. (1968). GEEN TITEL OPGEGEVEN J.Amer.Chem.Soc.. 90 pag.: 4011
    • M.T. Reetz, K. Kesseler, A. Jung. (1984). GEEN TITEL OPGEGEVEN Tetrahydron Lett.. 25 pag.: 729
21. D.A. Evans, J.L. Duffy, M.J. Dart. (1994). GEEN TITEL OPGEGEVEN Tetrahydron Lett.. 35 pag.: 8537
22. D.A. Evans, M.J. Dart, J.L. Duffy, M.G. Yang. (1996). GEEN TITEL OPGEGEVEN J.Amer.Chem.Soc.. 118 pag.: 4322