Fórmula de Bethe
Partículas rápidas carregadas movendo-se através da matéria interagem com os elétrons dos átomos no material. A interação excita ou ioniza os átomos. Isso leva a uma perda de energia das partículas em movimento. A fórmula de Bethe descreve[1] a média da perda de energia por distância percorrida das partículas carregadas (prótons, partículas alfa, íons atômicos, mas não elétrons[Footnote 1]) atravessando a matéria (ou, alternativamente, o "poder de parada" do material). A versão não-relativística foi encontrada por Hans Bethe, em 1930; a versão relativística (abaixo) foi encontrada por ele em 1932.[2] A perda de energia mais provável difere da perda de energia média, e é descrita pela distribuição de Landau-Vavilove.[3]
A fórmula de Bethe é, eventualmente, chamada de "Bethe-Bloch fórmula", mas isso é enganoso (ver abaixo).
A fórmula
[editar | editar código-fonte]Para uma partícula com velocidade v, carga z (em múltiplos da carga do elétron), e energia E, viajando a uma distância x na direção de um alvo composto de elétrons de densidade numérica n e potencial médio de excitação I, a versão relativística da fórmula lida em unidades do SI é:[2]
, (1)
onde c é a velocidade da luz e ε0, a permissividade do vácuo, , e e me, respectivamente, a carga do elétron e a massa de repouso.
Aqui, a densidade numérica de elétrons do material pode ser calculada por
onde ρ é a densidade do material; Z, seu número atômico; A, sua massa atômica relativa; NA, o número de Avogadro e Mu, a massa Molar constante.
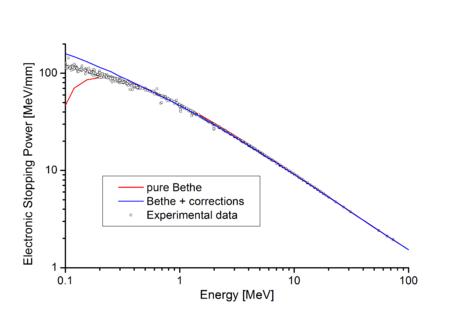
Na figura à direita, os pequenos círculos são resultados experimentais obtidos a partir de medições de vários cientistas, enquanto que a curva vermelha é a fórmula de Bethe.[4] Evidentemente, a teoria de Bethe concorda muito bem com experiência em alta energia. A concordância é melhor ainda quando as correções são aplicadas (ver abaixo).
Para baixas energias, por exemplo, para pequenas velocidades das partículas β << 1, a fórmula de Bethe se reduz a
(2)
Isso pode ser visto substituindo ßc por v na eq. (1) e, em seguida, negligenciando β2 devido ao seu pequeno tamanho.
Portanto, em baixas energias, a perda de energia de acordo com a fórmula de Bethe diminui aproximadamente como v-2 com o aumento da energia. Ela atinge um mínimo em, aproximadamente, E = 3Mc2, onde M é a massa da partícula (para prótons, seria algo em torno de 3000 MeV). Para muitos casos relativísticos β ≈ 1, a perda de energia aumenta novamente, mas de forma logarítmica devido à componente transversal do campo elétrico.
O potencial médio de excitação
[editar | editar código-fonte]
Na teoria de Bethe, o material é completamente descrito por um único número, o potencial médio de excitação I. Em 1933, Felix Bloch mostrou que a média do potencial de ionização dos átomos é aproximadamente dada por:
I = (10 eV) . Z, (3)
onde Z é o número atômico dos átomos do material. Se esta aproximação é introduzida na fórmula (1) acima, obtém-se uma expressão que é muitas vezes chamadoa de Bethe-Bloch fórmula. Mas desde que nós temos agora tabelas com valores precisos de I como uma função de Z (ver abaixo), podemos usá-las para obter melhores resultados do que a utilização da fórmula (3).
A figura mostra valores normalizados de I, tomados a partir de uma tabela.[5] Os picos e vales na figura levam a correspondentes vales e picos no "poder de parada". Estes são chamados de "Z2-oscilações" ou "Z2-estrutura" (onde Z2 = Z significa o número atômico do alvo).
Correções para a fórmula de Bethe
[editar | editar código-fonte]A fórmula de Bethe é válida apenas para as altas energias suficientes para que a partícula atômica carregada (íon) não transporte quaisquer elétrons atômicos com ele. Em energias menores, quando o íon transporta elétrons, isto reduz a sua carga de forma eficaz, e o poder de parada é consequentemente reduzido. Mas mesmo se o átomo estiver totalmente ionizado, correções fazem-se necessárias.
Bethe encontrou a sua fórmula usando a teoria de perturbação de mecânica quântica. Por isso, o seu resultado é proporcional ao quadrado da carga z da partícula. A descrição pode ser melhorada considerando correções que correspondem às maiores potências de z. Estas são: o efeito de Barkas-Andersen (proporcional a z3, depois de Walter H. Barkas e Hans Henrik Andersen), e a correção de Bloch (proporcional a z4). Além disso, tem-se que levar em conta que os elétrons atômicos do material não são estacionários ("shell correction").
A introdução da correção de Bloch pode ser outra razão para o nome comumente usado "fórmula de Bethe-Bloch". Mas, logicamente, seria mais justo nomeá-la de "fórmula de Bethe-Barkas-Andersen-Bloch", mas ninguém o faz.
As correções mencionadas foram construídas para os programas PSTAR e ASTAR, por exemplo, através do qual pode-se calcular o "poder de parada" para prótons e partículas alfa.[6] As correções são grandes em baixas energias e se tornam cada vez menores conforme a energia aumenta.
A energias muito altas, a correção da densidade de Fermi[5] tem que ser também adicionada.
O problema de nomenclatura
[editar | editar código-fonte]Na descrição de programas PSTAR e ASTAR, o National Institute of Standards and Technology[6] chama a fórmula (1) de "Bethe's stopping power fórmula".
Por outro lado, em 2008, na Review of Particle Physics,[7] a fórmula foi chamada de "Bethe-Bloch equation", apesar da expressão de Bloch (3) sequer aparecer na fórmula. Mas em edições mais recentes, a fórmula foi denominada simplesmente de "fórmula de Bethe".[8][9] Presumivelmente, o "Bloch" em "Bethe-Bloch" significava a "correção de Bloch" (mencionada acima). Em todo caso, a designação "Bethe-Barkas-Bloch" parecia mais lógica.
Veja também
[editar | editar código-fonte]Notas
[editar | editar código-fonte]- ↑ Para elétrons, a perda de energia é suavemente distinta devido a sua pequena massa e a sua indistinguibilidade (indistinguishability), e assim eles sofrem perdas maiores por Bremsstrahlung
Referências
[editar | editar código-fonte]- ↑ H. Bethe und J. Ashkin in "Experimental Nuclear Physics, ed.
- ↑ a b Sigmund, Peter Particle Penetration and Radiation Effects.
- ↑ H. Bichsel, Rev.
- ↑ «Stopping Power for Light and Heavier Ions». 15 de abril de 2015. Consultado em 1 de novembro de 2015
- ↑ a b Report 49 of the International Commission on Radiation Units and Measurements, "Stopping Powers and Ranges for Protons and Alpha Particles", Bethesda, MD, USA (1993)
- ↑ a b NISTIR 4999, Stopping Power and Range Tables
- ↑ 2008 Review of Particle Physics, C. Amsler et al., Physics Letters B 667 (2008) 1
- ↑ K. Nakamura et al.
- ↑ J. Beringer et al.
![{\displaystyle -\left\langle {\frac {dE}{dx}}\right\rangle ={\frac {4\pi }{m_{e}c^{2}}}\cdot {\frac {nz^{2}}{\beta ^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}c^{2}\beta ^{2}}{I\cdot (1-\beta ^{2})}}\right)-\beta ^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dd473093a5b5e89894bd589a0a2f58c669ed1b7)


![{\displaystyle -{\frac {dE}{dx}}={\frac {4\pi nz^{2}}{m_{e}v^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}v^{2}}{I}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49ffd089c1ec85c3cafa26ad6104042d0151eb94)