Pavare trihexagonală
| Pavare trihexagonală | |
 | |
| Descriere | |
|---|---|
| Tip | pavare uniformă |
| Configurația vârfului | (3.6)2 |
| Simbol Wythoff | 2 | 6 3 3 3 | 3 |
| Simbol Schläfli | r{6,3} sau h2{6,3} |
| Diagramă Coxeter | |
| Grup de simetrie | p6m, [6,3], (*632) |
| Grup de rotație | p6, [6,3]+, (632) p3, [3[3]]+, (333) |
| Poliedru dual | pavare rombică |
| Proprietăți | tranzitivă pe vârfuri și pe laturi |
| Figura vârfului | |
 | |
În geometrie pavarea trihexagonală este una dintre cele 11 pavări uniforme ale planului euclidian cu poligoane regulate.[1] Este formată din triunghiuri echilaterale și hexagoane regulate, aranjate astfel încât fiecare hexagon să fie înconjurat de triunghiuri și invers. Numele derivă din faptul că combină o pavare hexagonală regulată și o pavare triunghiulară. Două hexagoane și două triunghiuri alternează în jurul fiecărui vârf, iar laturile acestora formează un aranjament infinit de linii. Pavarea duală este pavarea rombică.[2]
Acest model și locul său în clasificarea pavărilor uniforme erau deja cunoscute de Johannes Kepler, după cum apare în cartea sa din 1619, Harmonices Mundi.[3] Modelul a fost folosit de mult în Japonia pentru coșuri împletite, unde este numit „kagome”. Termenul japonez pentru acest model a fost preluat în fizică, unde este numit „rețea Kagome”. Apare și în structurile cristaline ale anumitor minerale.
Kagome
[modificare | modificare sursă]
Kagome este un model de împletitură de bambus tradițională japoneză; numele său este compus din cuvintele „kago”, care înseamnă „coș”, și „me”, care înseamnă „ochi”, referindu-se la modelul găurilor dintr-un coș împletit.

Este un aranjament de triunghiuri întrețesute astfel încât fiecare punct în care două șipci se încrucișează să aibă patru puncte învecinate, formând modelul unei pavări trihexagonale. Procesul împletirii conferă modelului Kagome o simetrie chirală a grupului de tapet(d) p6, (632).

Rețeaua Kagome
[modificare | modificare sursă]Termenul de „rețea kagome” a fost inventat de fizicianul japonez Kôdi Husimi și a apărut pentru prima dată într-o lucrare din 1951 a asistentului său, Ichirō Shōji.[4] În acest sens rețeaua kagome constă din vârfurile și laturile pavărilor trihexagonale. În ciuda numelui, aceste puncte de trecere nu formează o rețea matematică.
O structură tridimensională înrudită, formată din vârfurile și laturile fagurelui cubic pe sfert, umplând spațiul cu tetraedre regulate și tetraedre trunchiate, a fost numită rețea hiperkagome.[5] Rețeaua conține patru seturi de plane paralele de puncte și drepte, fiecare plan fiind o rețea kagome bidimensională. O a doua expresie tridimensională are straturi paralele de rețele bidimensionale și se numește rețea kagome ortorrombică.[5] Fagurele prismatic trihexagonal reprezintă laturile și vârfurile sale.
Unele minerale, cum ar fi jarozitul(d) și herbertsmithitul(d), conțin straturi bidimensionale sau aranjament tridimensional al rețelei kagome de atomi în structura lor cristalină. Aceste minerale prezintă proprietăți fizice noi legate de magnetism. De exemplu, aranjamentul de spin al ionilor magnetici din Co3V2O8 este o rețea kagome care prezintă un comportament magnetic particular la temperaturi scăzute.[6] S-a descoperit că magneții cuantici realizați din metale Kagome(d) prezintă multe fenomene electronice și magnetice neașteptate.[7][8][9][10]
Simetrie
[modificare | modificare sursă]
Pavarea trihexagonală are simbolul Schläfli r{6,3} și diagrama Coxeter ![]()
![]()
![]()
![]()
![]() , simbolizând faptul că este o pavare hexagonală, {6,3}, rectificată. Simetriile pot fi descrise de grupul de tapet p6mm, (*632),[11] iar pavarea poate fi derivată prin construcția Wythoff din domeniile fundamentale de reflexie ale acest grup. Pavarea trihexagonală este o pavare cvasiregulată, alternând două tipuri de poligoane, cu configurația vârfului (3.6)2. Este, de asemenea, o pavare uniformă, una dintre cele opt derivate din pavarea hexagonală regulată.
, simbolizând faptul că este o pavare hexagonală, {6,3}, rectificată. Simetriile pot fi descrise de grupul de tapet p6mm, (*632),[11] iar pavarea poate fi derivată prin construcția Wythoff din domeniile fundamentale de reflexie ale acest grup. Pavarea trihexagonală este o pavare cvasiregulată, alternând două tipuri de poligoane, cu configurația vârfului (3.6)2. Este, de asemenea, o pavare uniformă, una dintre cele opt derivate din pavarea hexagonală regulată.
Colorare uniformă
[modificare | modificare sursă]Există două colorări uniforme diferite ale unei pavări trihexagonale. Identificarea culorilor prin indici de pe cele 4 fețe din jurul unui vârf (3.6.3.6) este: 1212, 1232.[1] A doua se numește pavare hexagonală cantelată, h2{6,3}, cu triunghiuri de două culori, existente în simetria grupului de tapet p3m1 (*333).
| Simetrie | p6m, (*632) | p3m, (*333) |
|---|---|---|
| Colorare | 
|

|
| domeniu fundamental |
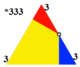
| |
| Wythoff | 2 | 6 3 | 3 3 | 3 |
| Coxeter | ||
| Schläfli | r{6,3} | r{3[3]} = h2{6,3} |
Împachetarea cercurilor
[modificare | modificare sursă]
Pavarea trihexagonală poate fi folosită la împachetarea cercurilor, plasând cercuri cu diametru egal în centrul fiecărui punct.[12] Fiecare cerc este în contact cu alte 4 cercuri din împachetare (număr de contacte).
Pavări echivalente topologic
[modificare | modificare sursă]Pavarea trihexagonală poate fi distorsionată geometric în pavări echivalente din punct de vedere topologic, cu simetrie inferioară.[1] În aceste variante de pavări, laturile nu se aliniază neapărat pentru a forma drepte.
| p3m1, (*333) | p3, (333) | p31m, (3*3) | cmm, (2*22) | |||
|---|---|---|---|---|---|---|

|

|

|

|

|

|

|
Pavări cvasiregulate înrudite
[modificare | modificare sursă]Pavarea trihexagonală există într-o succesiune de simetrii de pavări cvasiregulate cu configurația vârfurilor (3.n)2, mergând de la pavările sferei la cele ale planului euclidian și ale planului hiperbolic. Cu notația orbifold de simetrie *n32 toate aceste pavări sunt construcții Wythoff într-un domeniu fundamental de simetrie, cu puncte generatoare în colțul în unghi drept al domeniului.[13][14]
| Pavări cvasiregulate cu simetrii orbifold *n32: (3.n)2 | |||||||
|---|---|---|---|---|---|---|---|
Construcție |
Sferic | Euclidian | Hiperbolic | ||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |
| Figuri cvasiregulate |

|

|

|

|

|

|

|
| Vârf | (3.3)2 | (3.4)2 | (3.5)2 | (3.6)2 | (3.7)2 | (3.8)2 | (3.∞)2 |
Apeirogoane complexe regulate înrudite
[modificare | modificare sursă]Există 2 apeirogoane complexe regulate, care au în comun vârfurile pavării trihexagonale. Apeirogoanele complexe regulate au vârfuri și laturi, unde laturile pot conține 2 sau mai multe vârfuri. Apeirogoanele regulate p{q}r sunt constrânse de: 1/p + 2/q + 1/r = 1. Laturile au vârfurile p aranjate ca un poligon regulat, iar figura vârfului este r-gonală.[15]
Prima are laturi triunghiulare, câte două în jurul fiecărui vârf, iar a doua are laturi hexagonale, tot câte două în jurul fiecărui vârf.

|

|
| 3{12}2 or |
6{6}2 or |
|---|
Note
[modificare | modificare sursă]- ^ a b c en Grünbaum, Branko; Shephard, G. C. (). Tilings and Patterns
 . W. H. Freeman. ISBN 978-0-7167-1193-3. A se vedea teorema 2.1.3, p. 59 (clasificarea pavărilor uniforme); figura 2.1.5, p.63 (ilustrarea acestei pavări), teorema 2.9.1, p. 103 (clasificarea pavărilor colorate), figura 2.9.2, p. 105 (ilustrarea pavărilor colorate), figura 2.5.3(d), p. 83 (pavarea stelată echivalentă topologic) și exercițiul 4.1.3, p. 171 (echivalența topologică a pavărilor trihexagonale și cu două triunghiuri).
. W. H. Freeman. ISBN 978-0-7167-1193-3. A se vedea teorema 2.1.3, p. 59 (clasificarea pavărilor uniforme); figura 2.1.5, p.63 (ilustrarea acestei pavări), teorema 2.9.1, p. 103 (clasificarea pavărilor colorate), figura 2.9.2, p. 105 (ilustrarea pavărilor colorate), figura 2.5.3(d), p. 83 (pavarea stelată echivalentă topologic) și exercițiul 4.1.3, p. 171 (echivalența topologică a pavărilor trihexagonale și cu două triunghiuri).
- ^ en Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications, Inc., 1979, ISBN: 0-486-23729-X, p. 38
- ^ en Aiton, E. J.; Duncan, Alistair Matheson; Field, Judith Veronica, ed. (), The Harmony of the World by Johannes Kepler, Memoirs of the American Philosophical Society, 209, American Philosophical Society, pp. 104–105, ISBN 9780871692092
- ^ en Mekata, Mamoru (februarie 2003). „Kagome: The story of the basketweave lattice”. Physics Today. 56 (2): 12–13. Bibcode:2003PhT....56b..12M. doi:10.1063/1.1564329
 .
.
- ^ a b en Lawler, Michael J.; Kee, Hae-Young; Kim, Yong Baek; Vishwanath, Ashvin (). „Topological spin liquid on the hyperkagome lattice of Na4Ir3O8”. Physical Review Letters. 100 (22): 227201. arXiv:0705.0990
 . Bibcode:2008PhRvL.100v7201L. doi:10.1103/physrevlett.100.227201. PMID 18643453.
. Bibcode:2008PhRvL.100v7201L. doi:10.1103/physrevlett.100.227201. PMID 18643453.
- ^ en Yen, F., Chaudhury, R. P., Galstyan, E., Lorenz, B., Wang, Y. Q., Sun, Y. Y., Chu, C. W. (). „Magnetic phase diagrams of the Kagome staircase compound Co3V2O8”. Physica B: Condensed Matter. 403 (5–9): 1487–1489. arXiv:0710.1009
 . Bibcode:2008PhyB..403.1487Y. doi:10.1016/j.physb.2007.10.334.
. Bibcode:2008PhyB..403.1487Y. doi:10.1016/j.physb.2007.10.334.
- ^ en „A quantum magnet with a topological twist”. Discovery: Research at Princeton (în engleză). . Accesat în .
- ^ en Yin, Jia-Xin; Zhang, Songtian S.; Li, Hang; Jiang, Kun; Chang, Guoqing; Zhang, Bingjing; Lian, Biao; Xiang, Cheng; Belopolski (). „Giant and anisotropic many-body spin–orbit tunability in a strongly correlated kagome magnet”. Nature. 562 (7725): 91–95. arXiv:1810.00218
 . Bibcode:2018Natur.562...91Y. doi:10.1038/s41586-018-0502-7. PMID 30209398.
. Bibcode:2018Natur.562...91Y. doi:10.1038/s41586-018-0502-7. PMID 30209398.
- ^ en Yin, Jia-Xin; Zhang, Songtian S.; Chang, Guoqing; Wang, Qi; Tsirkin, Stepan S.; Guguchia, Zurab; Lian, Biao; Zhou, Huibin; Jiang, Kun; Belopolski, Ilya; Shumiya, Nana (). „Negative flat band magnetism in a spin–orbit-coupled correlated kagome magnet”. Nature Physics. 15 (5): 443–8. arXiv:1901.04822
 . Bibcode:2019NatPh..15..443Y. doi:10.1038/s41567-019-0426-7.
. Bibcode:2019NatPh..15..443Y. doi:10.1038/s41567-019-0426-7.
- ^ en Yazyev, Oleg V. (). „An upside-down magnet”. Nature Physics. 15 (5): 424–5. Bibcode:2019NatPh..15..424Y. doi:10.1038/s41567-019-0451-6.
- ^ en Steurer, Walter; Deloudi, Sofia (). Crystallography of Quasicrystals: Concepts, Methods and Structures. Springer Series in Materials Science. 126. Springer. p. 20. ISBN 9783642018992.
- ^ en Critchlow, Keith () [1969]. „pattern G”. Order in Space: A design source book. Thames & Hudson. pp. 74–75. ISBN 9780500340332.
- ^ en Coxeter, H.S.M. (). „V. The Kaleidoscope, §5.7 Wythoff's construction”. Regular Polytopes (ed. 3rd). Dover. ISBN 0-486-61480-8.
- ^ Huson, Daniel H. „Two Dimensional symmetry Mutations”. CiteSeerX 10.1.1.30.8536
 .
.
- ^ en Coxeter, H.S.M. (). Regular Complex Polytopes (ed. 2nd). Cambridge University Press. pp. 111–2, 136. ISBN 9780521394901.
Lectură suplimentară
[modificare | modificare sursă]- en Seymour, Dale; Britton, Jill (). Introduction to Tessellations. pp. 50–56. ISBN 978-0866514613.
Vezi și
[modificare | modificare sursă]Legături externe
[modificare | modificare sursă] Materiale media legate de pavare trihexagonală la Wikimedia Commons
Materiale media legate de pavare trihexagonală la Wikimedia Commons


