Đường thẳng Droz-Farny

Đường thẳng qua các điểm ${\displaystyle A_{0},B_{0},C_{0}}$ là đường thẳng Droz-Farny

Trong hình học phẳng, đường thẳng Droz-Farny nói về một tính chất của hai đường thẳng vuông góc cắt nhau tại trực tâm của một tam giác bất kỳ. Nội dung như sau:

Cho tam giác ${\displaystyle ABC}$, và ${\displaystyle H}$ là trực tâm (trực tâm là điểm đồng quy của ba đường cao trong tam giác). Nếu như hai đường thẳng ${\displaystyle d_{1}}$ và ${\displaystyle d_{2}}$ vuông góc với nhau tại ${\displaystyle H}$. Ta đặt ${\displaystyle A_{1}}$, ${\displaystyle B_{1}}$, và ${\displaystyle C_{1}}$ lần lượt là các giao điểm của ${\displaystyle d_{1}}$ với các cạnh ${\displaystyle BC}$, ${\displaystyle CA}$, và ${\displaystyle AB}$. Tương tự ta đặt ${\displaystyle A_{2}}$, ${\displaystyle B_{2}}$, and ${\displaystyle C_{2}}$ lần lượt là các giao điểm của ${\displaystyle d_{2}}$ với các cạnh của tam giác ${\displaystyle BC}$, ${\displaystyle CA}$, and ${\displaystyle AB}$. Định lý đường thẳng Droz-Farny khẳng định rằng trung điểm các đoạn thẳng ${\displaystyle A_{1}A_{2}}$, ${\displaystyle B_{1}B_{2}}$, và ${\displaystyle C_{1}C_{2}}$ thẳng hàng.^[1][2][3]

Định lý được phát biểu bởi Arnold Droz-Farny năm 1899,^[1] nhưng không được chứng minh.^[4]

Tổng quát của Goormaghtigh

Một tổng quát của đường thẳng Droz-Farny đưa ra và chứng minh bởi René Goormaghtigh năm 1930.^[5]. Định lý Goormaghtigh phát biểu rằng: Cho tam giác ${\displaystyle ABC}$ và điểm ${\displaystyle P}$ trên đường thằng ${\displaystyle d}$, các đường thẳng đối xứng của ${\displaystyle PA,PB,PC}$ qua đường thẳng ${\displaystyle d}$ cắt các cạnh ${\displaystyle BC,CA,AB}$ lần lượt tại ${\displaystyle A_{0},B_{0},C_{0}}$ thì ${\displaystyle A_{0},B_{0},C_{0}}$ thẳng hàng. Khi điểm ${\displaystyle P}$ tại trực tâm của tam giác, đường thẳng này trở thành đường thẳng Droz-Farny.

Tổng quát của Đào

Đào tổng quát định lý Goormaghtigh

Kết quả tiếp tục được mở rộng bởi Đào Thanh Oai. Mở rộng này có thể được hiểu như sau:

Mở rộng thứ nhất: Nếu trung điểm của các đoạn thẳng song song AA', BB', CC' nằm trên đường thẳng chứa điểm D. Khi đó ba đường thẳng DA', DB', DC' lần lượt cắt ba cạnh BC, CA, AB tại ba điểm thẳng hàng.^[6] Kết quả tiếp tục được mở rộng như sau:

Trường hợp điểm D nằm trên đường thẳng đối cực của P

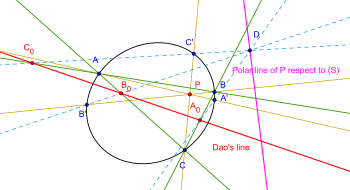
Mở rộng tổng quát: Cho đường conic (S) và điểm ${\displaystyle P}$ trên mặt phẳng, ba đường thẳng qua ${\displaystyle P}$ cắt đường conic lần lượt tại các điểm ${\displaystyle A,A'}$; ${\displaystyle B,B'}$; ${\displaystyle C,C'}$. Cho ${\displaystyle D}$ là một điểm nằm trên đường thẳng đối cực của ${\displaystyle P}$ hoặc trên đường conic (S) thì ${\displaystyle DA',DB',DC'}$ lần lượt cắt ba cạnh ${\displaystyle BC,CA,AB}$ tại ba điểm ${\displaystyle A_{0},B_{0},C_{0}}$ thẳng hàng. Hơn thế bốn điểm ${\displaystyle A_{0},B_{0},C_{0},P}$ thẳng hàng khi và chỉ khi ${\displaystyle D}$ nằm trên đường conic (S).^[7][8][9]

Xem thêm

• Định lý Đào

Tham khảo

1. ^ A. Droz-Farny (1899), Question 14111 The Educational Times, volume 71, pages 89-90
2. Jean-Louis Ayme (2004), A Purely Synthetic Proof of the Droz-Farny Line Theorem Lưu trữ 2020-07-16 tại Wayback Machine. Forum Geometricorum, volume 14, pages 219–224, ISSN 1534-1178
3. Floor van Lamoen and Eric W. Weisstein (), Droz-Farny Theorem at Mathworld
4. J. J. O'Connor and E. F. Robertson (2006), Arnold Droz-Farny. The MacTutor History of Mathematics archive. Online document, accessed on 2014-10-05.
5. René Goormaghtigh (1930), Sur une généralisation du théoreme de Noyer, Droz-Farny et Neuberg. Mathesis, volume 44, page 25
6. Son Tran Hoang (2014), A synthetic proof of Dao's generalization of Goormaghtigh's theorem Lưu trữ 2014-10-06 tại Wayback Machine. Global Journal of Advanced Research on Classical and Modern Geometries, volume 3, pages 125–129, ISSN 2284-5569
7. “Nguyen Ngoc Giang, A proof of Dao theorem, Global Journal of Advanced Research on Classical and Modern Geometries, ISSN: 2284-5569, Vol.4, (2015), Issue 2, page 102-105”. Bản gốc lưu trữ ngày 6 tháng 10 năm 2014. Truy cập ngày 20 tháng 10 năm 2014.
8. Geoff Smith (2015). 99.20 A projective Simson line. The Mathematical Gazette, 99, pp 339-341. doi:10.1017/mag.2015.47
9. O.T.Dao 29-July-2013, Two Pascals merge into one, Cut-the-Knot