Định luật Hess
Trong hóa lý, định luật Hess phát biểu rằng toàn bộ biến thiên enthalpy trong toàn bộ quá trình phản ứng hóa học không phụ thuộc vào trình tự các bước được thực hiện.[1][2] Tên của định luật được đặt theo nhà hóa học và bác sĩ người Nga gốc Thụy Sĩ tên là Germain Hess, người đã đề xuất định luật này vào năm 1840.
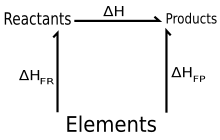
Định luật Hess hiểu là một cách diễn giải của bản chất enthalpy rằng: enthalpy của một phản ứng hóa học không phụ thuộc vào quá trình, chỉ phụ thuộc vào trạng thái đầu và trạng thái cuối (enthalpy là một hàm trạng thái). Theo nguyên lý thứ nhất của nhiệt động lực học, biến thiên enthalpy trong một hệ do phản ứng ở áp suất không đổi bằng với lượng nhiệt hấp thụ (hoặc số đối của lượng nhiệt tỏa ra), có thể được xác định bằng phép đo nhiệt lượng cho nhiều phản ứng. Các giá trị biến thiên enthalpy thường được quy ước tại điều kiện có cùng nhiệt độ và áp suất ban đầu và cuối cùng (trong khi các điều kiện được phép thay đổi trong quá trình phản ứng). Định luật Hess có thể được sử dụng để xác định tổng năng lượng cần thiết cho một phản ứng hóa học bằng cách chia thành các bước tổng hợp dễ mô tả hơn, cho phép tìm ra enthalpy tạo thành chuẩn phục vụ dự đoán sự thay đổi enthalpy trong các tổng hợp hóa học phức tạp.
Định luật
[sửa | sửa mã nguồn]Định luật Hess phát biểu rằng sự thay đổi enthalpy trong phản ứng hóa học là như nhau bất kể phản ứng diễn ra theo một bước hay nhiều bước, miễn là trạng thái ban đầu và trạng thái cuối cùng của các chất phản ứng và sản phẩm là như nhau. Enthalpy là một đại lượng quảng tính, có nghĩa là giá trị của enthalpy tỷ lệ thuận với kích thước của hệ.[3] Do đó, sự thay đổi enthalpy tỷ lệ thuận với số mol chất tham gia phản ứng.
Định luật Hess cho phép tính toán biến thiên enthalpy () phản ứng khi không thể đo trực tiếp. Thực hiện các phép toán đại số cơ bản dựa trên các phương trình hóa học phản ứng hóa học sử dụng các giá trị đã xác định của enthalpy tạo thành chuẩn.
Phản ứng tỏa nhiệt thì biến thiên enthalpy có giá trị âm (), phản ứng có nhiều khả năng phản ứng xảy ra tự phát; phản ứng thu nhiệt thì biến thiên enthalpy có giá trị dương (). Chú ý rằng entropy cũng đóng một vai trò quan trọng trong việc xác định phản ứng có tự xảy ra hay không (tự phát), vì một số phản ứng có sự thay đổi enthalpy dương có thể tự xảy ra do khi phản ứng, entropy tăng.
Ứng dụng enthalpy tạo thành
[sửa | sửa mã nguồn]Theo định luật Hess, giá trị của đối với một phản ứng đơn lẻ có thể được tính toán từ enthalpy tạo thành chuẩn (của các sản phẩm và chất phản ứng. Giá trị enthalpy tạo thành chuẩn này được cho sẵn trong các tài liệu:
Trong đó
- enthalpy chuẩn của phản ứng được ký hiệu là hay ,
- Tổng đầu tiên là các chất sản phẩm (p là product) và tổng thứ hai là các chất phản ứng hay chất đầu (r là reactant),
- là hệ số trong phương trình hóa học của sản phẩm p sau cân bằng phương trình, là hệ số trong phương trình hóa học của chất tham gia r sau cân bằng phương trình,
- là enthalpy tạo thành của sản phẩm p, là enthalpy tạo thành của chất phản ứng r,
- Ký hiệu ⊖ biểu thị các giá trị trên được đo trong điều kiện chuẩn. còn được ký hiệu là . Điều kiện chuẩn khi:
- Áp suất: 1 atm (101.325 kPa) hoặc 1 bar (100.000 kPa)
- Nhiệt độ: 25 °C (298,15 K)
- Các nguyên tố hoặc hợp chất ở trạng thái vật lý (thể) bình thường, tức là trạng thái chuẩn. Ví dụ: oxy thì ở thể khí, nước ở thể lỏng, natri ở thể rắn.
Ví dụ
[sửa | sửa mã nguồn]Ví dụ 1
[sửa | sửa mã nguồn]- (a) Cgraphite + O2 → CO2(g) ( ΔH = −393.5 kJ/mol) (bước trực tiếp)
- (b) Cgraphite + 1/2 O2 → CO(g) (ΔH = −110.5 kJ/mol)
- (c) CO(g) +1/2 O2 → CO2(g) (ΔH = −283.0 kJ/mol)
Phản ứng (a) là tổng của các phản ứng (b) và (c), trong đó tổng ΔH = −393,5 kJ/mol, bằng ΔH trong phản ứng (a).
Ví dụ 2
[sửa | sửa mã nguồn]Cho biết
- B2O3(s) + 3H2O(g) → 3O2(g) + B2H6(g) (ΔH = 2035 kJ/mol)
- H2O(l) → H2O(g) (ΔH = 44 kJ/mol)
- H2(g) + 1/2 O2(g) → H2O(l) (ΔH = −286 kJ/mol)
- 2B(s) + 3H2(g) → B2H6(g) (ΔH = 36 kJ/mol)
Tìm enthalpy tạo thành chuẩn (ΔHf) của B2O3 (s):
- 2B(s) + 3/2 O 2 (g) → B2O3 (s)
Sau khi nhân các phương trình (và biến thiên enthalpy của các phản ứng) với các thừa số thích hợp và đổi chiều phản ứng khi cần thiết, kết quả sẽ được:
- B2H6(g) + 3O2(g) → B2O3(s) + 3H2O(g) (ΔH = 2035 × (−1) = −2035 kJ/mol)
- 3H2O(g) → 3H2O(l) (ΔH = 44 × (−3) = −132 kJ/mol)
- 3H2O(l) → 3H2(g) + (3/2) O2(g) (ΔH = −286 × (−3) = 858 kJ/mol)
- 2B(s) + 3H2(g) → B2H6(g) (ΔH = 36 kJ/mol)
Cộng các phương trình này với nhau và lược bỏ các chất giống nhau ở hai phía mũi tên phản ứng, kết quả:
- 2B(s) + 3/2 O2(g) → B2O3(s) (ΔH = −1273 kJ/mol)
Năng lượng tự do Gibbs và entropy
[sửa | sửa mã nguồn]Định luật Hess có thể mở rộng để tính toán biến thiên entropy và năng lượng tự do Gibbs, vì đây cũng là các hàm trạng thái. Chu trình nhiệt động lực học Bordwell là một ví dụ.
Đối với năng lượng tự do:
Đối với entropy:
Ứng dụng
[sửa | sửa mã nguồn]Định luật Hess rất hữu ích trong việc xác định các enthalpy sau:[1]
- Enthalpy tạo thành của các chất trung gian không ổn định, ví dụ: CO(g) và NO(g).
- Biến thiên enthalpy trong quá trình chuyển pha (Nhiệt chuyển pha) và chuyển thù hình.
- Năng lượng mạng tinh thể của các chất ion bằng chu trình Born–Haber nếu đã biết ái lực electron để tạo thành anion.
- Ái lực electron bằng cách sử dụng chu trình Born–Haber khi đã biết năng lượng mạng tinh thể (ngược lại của ý (3)).
Xem thêm
[sửa | sửa mã nguồn]- Nhiệt hóa học
- Nhiệt động lực học (hay nhiệt động học)
Tham khảo
[sửa | sửa mã nguồn]- ^ a b Mannam Krishnamurthy; Subba Rao Naidu (2012). “7”. Trong Lokeswara Gupta (biên tập). Chemistry for ISEET - Volume 1, Part A (ấn bản thứ 2012). Hyderabad, India: Varsity Education Management Limited. tr. 244.
- ^ “Hess' Law - Conservation of Energy”. University of Waterloo. Bản gốc lưu trữ ngày 9 tháng 1 năm 2015. Truy cập ngày 12 tháng 1 năm 2014.
- ^ Engel, Thomas; Reid, Philip (2006). Physical Chemistry. Pearson / Benjamin Cummings. tr. 6. ISBN 0-8053-3842-X.
A variable ... proportional to the size of the system is referred to as an extensive variable.
- Chakrabarty, D.K. (2001). An Introduction to Physical Chemistry. Mumbai: Alpha Science. tr. 34–37. ISBN 1-84265-059-9.
Đọc thêm
[sửa | sửa mã nguồn]- Leicester, Henry M. (1951). “Germain Henri Hess and the Foundations of Thermochemistry”. The Journal of Chemical Education. 28 (11): 581–583. Bibcode:1951JChEd..28..581L. doi:10.1021/ed028p581.
Liên kết ngoài
[sửa | sửa mã nguồn]- Hess' paper (1840) on which his law is based (at ChemTeam site)
- a Hess' Law experiment Lưu trữ 2016-03-03 tại Wayback Machine
 GIẢM
50%
GIẢM
50%
 GIẢM
33%
GIẢM
33%
 GIẢM
24%
GIẢM
24%
 GIẢM
30%
GIẢM
30%
 GIẢM
33%
GIẢM
33%














![[Tóm tắt và đánh giá] Bạn không thông minh lắm đâu | Cuốn sách tâm lý học thú vị bạn nên đọc vào năm 2024](https://down-bs-vn.img.susercontent.com/vn-11134201-23030-c1d4ivny4kov19.webp)