Giá trị nốt nhạc

Giá trị nốt nhạc có ý nghĩa chỉ ra trường độ tương đối của nốt nhạc thông sự kết hợp của các yếu tố như: màu sắc của thân nốt nhạc (đen hoặc trắng), nốt nhạc có đuôi không và nốt nhạc có dấu móc không.

Dấu lặng được dùng chỉ tạo một khoảng lặng có trường độ bằng với giá trị nốt nhạc tương ứng.

Bảng tóm tắt

Dấu lặng	Tên gọi	Giá trị	Có một chấm dôi	Có hai chấm dôi	Có ba chấm dôi
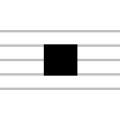	Nốt tròn tư	8	8 + 4	8 + 4 + 2	8 + 4 + 2 + 1
	Nốt tròn ba	4	4 + 2	4 + 2 + 1	4 + 2 + 1 + 1/2
	Nốt tròn đôi	2	2 + 1	2 + 1 + 1/2	2 + 1 + 1/2 + 1/4
	Nốt tròn	1	1 + 1/2	1 + 1/2 + 1/4	1 + 1/2 + 1/4 + 1/8
	Nốt trắng	1/2	1/2 + 1/4	1/2 + 1/4 + 1/8	1/2 + 1/4 + 1/8 + 1/16
hoặc	Nốt đen	1/4	1/4 + 1/8	1/4 + 1/8 + 1/16	1/4 + 1/8 + 1/16 + 1/32
	Nốt móc đơn	1/8	1/8 + 1/16	1/8 + 1/16 + 1/32	1/8 + 1/16 + 1/32 + 1/64
	Nốt móc kép	1/16	1/16 + 1/32	1/16 + 1/32 + 1/64	1/16 + 1/32 + 1/64 + 1/128
	Nốt móc ba	1/32	1/32 + 1/64	1/32 + 1/64 + 1/128	1/32 + 1/64 + 1/128 + 1/256
	Nốt móc tư	1/64	1/64 + 1/128	1/64 + 1/128 + 1/256	1/64 + 1/128 + 1/256 + 1/512
	Nốt móc năm	1/128	1/128 + 1/256	1/128 + 1/256 + 1/512	1/128 + 1/256 + 1/512 + 1/1024
	Nốt móc sáu	1/256	1/256 + 1/512	1/256 + 1/512 + 1/1024	1/256 + 1/512 + 1/1024 + 1/2048

Biến thể

Nốt tròn đôi có một số biến thể như trong hình. Thỉnh thoảng nốt tròn ba được dùng để ghi lại một trường âm dài vô định, ở cuối bản nhạc chẳng hạn.

Đuôi nốt nhạc (nếu có) có thể hướng lên hoặc xuống (trừ trường hợp định sẵn như nốt tròn ba). Dấu móc luôn nằm bên phải đuôi nốt dù cho đuôi này hướng lên hay hướng xuống.

Dấu chấm dôi

Có thể kéo dài trường âm của nốt nhạc bằng cách thêm dấu chấm gọi là dấu chấm dôi sau nốt nhạc. Tác dụng của một dấu này là thêm một nửa trường độ của nốt nhạc vào nốt đó, tức nốt nhạc kèm một dấu chấm dôi sẽ có trường âm bằng 1,5 lần nốt ban đầu. Nếu gọi số lượng dấu chấm dôi là n thì nốt nhạc có n dấu chấm dôi sẽ có trường âm gấp ${\tfrac {2^{n}-1}{2^{n}}}$ lần so với nốt ban đầu.

Năm 1752, J.J. Quantz là người đầu tiên dùng dấu chấm dôi kép.^[1] Trong âm nhạc thế kỷ 18 và trước đó, giá trị do dấu chấm dôi kéo dài không thống nhất, ít hơn hay nhiều hơn (so với hiện đại) là còn tùy vào từng trường hợp.^[1]

Để chia giá trị nốt nhạc thành ba phần bằng nhau, hay tổng quát hơn là chia thành nhiều hơn hai phần thì có thể dùng liên ba (tuplet).

Lịch sử

Bình ca Gregoriano

Trong các bản chép nhạc bình ca Gregoriano thời sơ khai đã thấy xuất hiện các thân nốt nhạc với nhiều hình dạng rất đa dạng, các nốt có đuôi hoặc không có đuôi. Tuy nhiên, có học giả cho rằng các ký hiệu này không có ý nghĩa thể hiện các trường âm khác nhau mặc dù người thời đó có dùng dấu chấm dôi để kéo dài trường âm.^{[cần dẫn nguồn]}

"Ký hiệu nhạc đo lường được"

Khoảng năm 1250, Franco thành Köln sáng tạo ra các biểu tượng để thể hiện các trường âm khác nhau, mặc dù mối tương quan (tỉ lệ) giữa các giá trị nốt nhạc khác nhau vẫn chưa thống nhất, phổ biến nhất là 3. Chuyên luận Ars nova của Philippe de Vitry (1320) có nêu một hệ thống tỉ lệ giữa các giá trị nốt nhạc khác nhau, đó có thể là 2:1 hoặc 3:1, kèm theo một hệ thống số chỉ nhịp "đo lường được" (mensural) nhằm phân biệt chúng.

Khoảng năm 1450, xuất hiện hệ thống ký nhạc mà trong đó tất cả giá trị nốt nhạc đều được thể hiện với đầu nốt vẽ bằng nét màu trắng. Trong cách ghi này, việc dùng liên ba được xác định thông qua màu sắc, chẳng hạn tô màu đen (hoặc thỉnh thoảng là đỏ) cho đầu nốt.

Khoảng năm 1600 thì nhìn chung người ta dùng hệ thống ký nhạc như hiện nay.

Tham khảo

^ ^a ^b Mục từ "Dotted notes" trong Harvard Dictionary of Music, ấn bản 2, tr. 242

[hvdi-1] Mục từ "Dotted notes" trong Harvard Dictionary of Music, ấn bản 2, tr. 242

[1]