Phép toán thao tác bit

Trong ngôn ngữ máy tính, các phép toán trên thao tác bit (tiếng Anh: bitwise operation) là các phép toán được thực hiện trên một hoặc nhiều chuỗi bit hoặc số nhị phân tại cấp độ của từng bit riêng biệt. Các phép toán này được thực hiện nhanh, ưu tiên, được hỗ trợ trực tiếp bởi vi xử lý, và được dùng để điều khiển các giá trị để tính toán.

Đối với các loại vi xử lý đời cũ, các phép toán trên thao tác bit thường nhanh hơn phép chia đáng kể, đôi khi nhanh hơn phép nhân, và đôi khi nhanh đáng kể hơn phép cộng, trong khi các vi xử lý hiện đại thường thực hiện phép nhân và phép cộng nhanh tương đương các phép toán trên thao tác bit do cấu trúc đường ống lệnh của chúng dài hơn. Cũng nhờ vào các lựa chọn trong thiết kế cấu trúc, các phép toán trên thao tác bit thường sử dụng ít tài nguyên hơn.

Các toán tử thao tác bit

Các toán tử thao tác bit (tiếng Anh: bitwise operator) là các toán tử được sử dụng chung với một hoặc hai số nhị phân để tạo ra một phép toán thao tác bit. Hầu hết các toán tử thao tác bit đều là các toán tử một hoặc hai ngôi.

Trong các giải thích dưới đây, bất kỳ dấu hiện nào của vị trí một bit được tính từ phía bên phải (nhỏ nhất), tiến dần về bên trái. Ví dụ: số nhị phân 0001 (số một trong hệ thập phân) có các số 0 ở mọi vị trí trừ vị trí đầu tiên.

AND

Toán tử thao tác bit AND lấy 2 toán hạng nhị phân có chiều dài bằng nhau và thực hiện phép toán lý luận AND trên mỗi cặp bit tương ứng bằng cách nhân chúng lại với nhau. Nhờ đó, nếu cả hai bit ở vị trí được so sánh đều là 1, thì bit hiển thị ở dạng nhị phân sẽ là 1 (1 x 1 = 1); ngược lại thì kết quả sẽ là 0 (1 x 0 = 0). Ví dụ:

A	B	A&B
0	0	0
0	1	0
1	0	0
1	1	1

  0101 (số thập phân 5)
AND 0011 (số thập phân 3)
 = 0001 (số thập phân 1)

Phép toán này có thể được sử dụng để xác định xem nếu một bit được thiết đặt (1) hoặc trống (0). Ví dụ: Cho trước dãy bit 0011 (số 3 trong hệ thập phân), để xác định xem bit thứ 2 có được thiết đặt hay không, ta sử phép toán thao tác bit AND với một dãy bit có chứa số 1 duy nhất ở bit thứ 2, ví dụ:

  0011 (số thập phân 3)
AND 0010 (số thập phân 2)
 = 0010 (số thập phân 2)

Vì kết quả 0010 là khác 0, ta biết là bit thứ 2 trong dãy bit ban đầu đã được thiết đặt. Điều này được gọi là che đậy bit. (Bằng phép loại suy, công dụng của mặt nạ, các phần không nên bị thay thế hoặc các phần không được quan tâm. Trong trường hợp này, các giá trị 0 che đậy cho các bit không được quan tâm).

Nếu ta lưu trữ kết quả, nó có thể được sử dụng để lưu trữ để xóa các bit được lựa chọn trong một thanh ghi. Cho ví dụ 0110 (số 6 trong hệ thập phân), bit thứ 2 có thể được xóa đi bằng cách sử dụng phép toán thao tác bit AND với dãy có một số 0 duy nhất ở bit thứ 2:

  0110 (số thập phân 6)
AND 1101 (số thập phân 13)  
 = 0100 (số thập phân 4)

Vì đặc tính này, việc kiểm tra tính chẵn lẻ của số nhị phân trở nên dễ dàng bằng cách kiểm tra giá trị của bit có giá trị thấp nhất. Sử dụng ví dụ phía trên ta có:

  0110 (số thập phân 6)
AND 0001 (số thập phân 1)  
 = 0000 (số thập phân 0)

Trong C, C++, Java, C#, toán tử thao tác bit AND được biểu diễn bằng ký hiệu "&" (dấu và):

x = y & z;

Trong Pascal, toán tử này là "and". Ví dụ:

x:= y and z;

NOT

Toán tử thao tác bit NOT, hay còn gọi là còn được gọi là toán tử lấy phần bù (complement), là toán tử một ngôi thực hiện phủ định luận lý trên từng bit, tạo thành bù 1 (one’s complement) của giá trị nhị phân cho trước. Bit nào là 0 thì sẽ trở thành 1, và 1 sẽ trở thành 0. Ví dụ:

NOT 0111 (số thập phân 7)
 = 1000 (số thập phân 8)

Bảng chân trị cho NOT:

A	NOT A
0	1
1	0

Phép toán thao tác bit lấy phần bù sẽ tương đương với bù 2 (two’s complement) của giá trị được tính trừ đi 1. Nếu phép toán bù 2 được sử dụng, như vậy:

NOT x = -x – 1

Đối với các số nguyên không âm, phép toán thao tác bit lấy phần bù của một số là "hình ảnh phản chiếu" của số đó tính tới điểm giữa của giới hạn số nguyên không âm. Vi dụ: đối với số nguyên 8-bit, NOT x = 255 – x, có thể được biểu diễn trên đồ thị dưới dạng một đường thẳng đi xuống mà đường thẳng đó "lật" một dãy tăng dần từ 0 đến 255, đến một dãy giảm dần từ 255 xuống 0. Một ví dụ đơn giản nhưng dễ hình dung là việc đảo ngược một hình ảnh trắng đen mà mỗi pixel trong đó được coi là một số nguyên không âm.

Trong các ngôn ngữ lập trình C, C++, Java, C#, toán tử thao tác bit NOT được biểu diễn bằng ký hiệu "~" (dấu ngã). Trong Pascal, toán tử này là "not". Ví dụ:

x = ~y; // C

Hay

x:= not y; { Pascal }

Câu lệnh trên sẽ gán cho x giá trị "NOT y" - tức phần bù của y. Chú ý rằng, toán tử này không tương đương với toán tử luận lý "not" (biểu diễn bằng dấu chấm than "!" trong C/C++). Về vấn đề này, xin xem ở bài toán tử hoặc các bài về ngôn ngữ C/C++.

Toán tử NOT hữu dụng khi ta cần tìm bù 1 của một số nhị phân. Nó cũng có thể được sử dụng làm bước đầu tiên để tìm số bù 2.

OR

Phép toán trên thao tác bit OR lấy hai dãy bit có độ dài bằng nhau và thực hiện phép toán lý luận bao hàm OR trên mỗi cặp bit tương ứng. Kết quả ở mỗi vị trí sẽ là 0 nếu cả hai bit là 0, ngược lại thì kết quả là 1. Ví dụ:

 0101 (số thập phân 5)
OR 0011 (số thập phân 3)
= 0111 (số thập phân 7)

Bảng chân trị cho OR:

A	B	A OR B
0	0	0
0	1	1
1	0	1
1	1	1

Trong C, C++, Java, C#, toán tử thao tác bit OR được biểu diễn bằng ký hiệu "|" (vạch đứng). Trong Pascal, toán tử này là "or". Ví dụ:

x = y | z; // C

Hay:

x:= y or z; { Pascal }

Câu lệnh trên sẽ gán cho x kết quả của "y OR z". Chú ý rằng toán tử này không tương đương với toán tử luận lý "or" (biểu diễn bằng cặp vạch đứng "||" trong C/C++). Về vấn đề này, xin xem ở bài toán tử hoặc các bài về ngôn ngữ C/C++.

Phép toán thao tác bit OR có thể được sử dụng để thiết đặt bit được chọn thành 1. Ví dụ: Nó có thể được sử dụng để bật (set) một bit (hoặc cờ) trong thanh ghi, trong đó mỗi bit đại diện cho một trạng thái trong phép logic đúng sai (boolean). Vì thế, 0010 (số 2 thập phân) có thể được xem là một bộ 4 cờ, trong đó cờ thứ nhất, thứ ba và thứ tư là trống (0) và cờ thứ hai được bật (1). Cờ thứ tư có thể được bật bằng cách thực hiện phép toán thao tác bit OR giữa giá trị này và một dãy bit với duy nhất bộ bit thứ 4:

 0010 (số thập phân 2)
OR 1000 (số thập phân 8)
 1010 (số thập phân 10)

Kỹ thuật này là một cách hiệu quả để lưu trữ một số trong những giá trị phép toán logic đúng sai (boolean) sử dụng ít bộ nhớ nhất có thể.

Khi làm việc với các máy không có nhiều không gian bộ nhớ trống, các lập trình viên thường áp dụng kĩ thuật trên. Lúc đó, thay vì khai báo tám biến kiểu bool (C++) độc lập, người ta sử dụng từng bit riêng lẻ của một byte để biểu diễn giá trị cho tám biến đó.

XOR

Phép toán thao tác bit XOR lấy hai dãy bit có cùng độ dài và thực hiện phép toán logic bao hàm XOR trên mỗi cặp bit tương ứng. Kết quả ở mỗi vị trí là 1 chỉ khi bit đầu tiên là 1 hoặc nếu chỉ khi bit thứ hai là 1, nhưng sẽ là 0 nếu cả hai là 0 hoặc cả hai là 1. Ở đây ta thực hiện phép so sánh hai bit, kết quả là 1 nếu hai bit khác nhau và là 0 nếu hai bit giống nhau. Ví dụ:

  0101 (số thập phân 5)
XOR 0011 (số thập phân 3)
  0110 (số thập phân 6)

(cách nhớ dễ nhất là: 2 bit giống nhau trả về 0, 2 bit khác nhau trả về 1)

Bảng chân trị cho XOR:

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

Phép toán thao tác bit XOR có thể được sử dụng để đảo ngược các bit được lựa chọn trong thanh ghi (còn được gọi là bật (set) hoặc lật (flip)). Bất kỳ bit nào được bật bằng cách thực hiện phép toán thao tác bit XOR nó với 1. Ví dụ: cho dãy bit 0010 (số 2 thập phân), bit thứ hai và thứ tư có thể được kích hoạt bằng cách sử dụng phép toán thao tác bit XOR với một dãy bit có chứa 1 ở vị trí thứ hai và thứ tư:

  0010 (số thập phân 2)
XOR 1010 (số thập phân 10)  
 = 1000 (số thập phân 8)

Kỹ thuật này có thể được sử dụng để điều khiển dãy bit biểu hiện các bộ chứa phép toán logic đúng sai (boolean).

Trong C, C++, Java, C#, toán tử thao tác bit XOR được biểu diễn bằng ký hiệu "^" (dấu mũ). Trong Pascal, toán tử này là "xor". Ví dụ:

x = y ^ z; // C

Hay:

x:= y xor z; { Pascal }

Câu lệnh trên sẽ gáp trình viên hợp ngữ (Assembly) thường sử dụng toán tử XOR để gán giá trị của một thanh ghi (register) về 0. Khi thực hiện phép toán XOR cho một mẫu bit với chính bản thân nó, mẫu nhị phân nhận được sẽ toàn bit 0. Trên nhiều kiến trúc máy tính, sử dụng XOR để gán 0 cho một thanh ghi sẽ được CPU xử lý nhanh hơn so với chuỗi thao tác tương ứng để nạp và lưu giá trị 0 vào thanh ghi.

Dịch chuyển và quay bit

Các phép dịch chuyển bit đôi khi được xem là các phép toán thao tác bit, bởi vì chúng sẽ xem một giá trị dưới dạng một dãy bit hơn là dưới dạng số lượng số (numerial quantity). Trong các phép toán này, các chữ số sẽ được di chuyển, hoặc dịch chuyển, sang trái hoặc phải. Các thanh ghi trong vi xử lý máy tính có độ dài cố định, vì vậy một vài bit sẽ bị "dịch chuyển ra ngoài" thanh ghi ở một đầu, trong khi đó thì một lượng bit tương ứng sẽ được "dịch chuyển vào" ở đầu còn lại; sự khác biệt ở các phép toán dịch chuyển bit nằm ở chỗ cách chúng xác định giá trị của các bit được dịch chuyển vào.

Dịch chuyển số học

Trong dịch chuyển số học, các bit được dịch chuyển ra khỏi đầu hoặc đuôi sẽ bị loại bỏ. Trong phép dịch chuyển số học về bên trái, các số 0 được dịch chuyển vào bên phải; trong phép dịch chuyển số học bên phải, bit thể hiện dấu được thêm vào bên trái, do đó dấu của số được giữ nguyên.

Ví dụ dưới đây sử dụng thanh ghi 8-bit:

 00010111 (số thập phân +23) Dịch chuyển trái
= 00101110 (số thập phân +46)

 10010111 (số thập phân -105) Dịch chuyển phải
= 11001011 (số thập phân -53)

Trường hợp đầu tiên, những số tận cùng bên trái được dịch chuyển khỏi thanh ghi, một số 0 mới được thêm vào cuối bên phải của thanh ghi. Trường hợp thứ hai, thành phần cuối bên phải đã được dịch chuyển ra khỏi, và số 1 được thêm vào bên trái, bảo toàn được dấu của số. Nhiều lần dịch chuyển có thể được rút ngắn lại còn một lần. Ví dụ:

 00010111 (số thập phân +23) Dịch sang trái 2 lần.
= 01011100 (số thập phân +92)

Dịch chuyển số học bên trái n lần tương đương nhân với 2ⁿ (nếu giá trị đó không gây tràn bộ nhớ), trong khi đó thì phép dịch chuyển số học sang phải n lần của một giá trị bù 2 thì tương đương với việc chia cho 2ⁿ và làm tròn về phía âm vô cùng. Nếu số nhị phân được xem là bù 1, thì phép dịch chuyển sang phải tương tự sẽ cho kết quả bằng với việc chia số đó cho 2ⁿ và làm tròn về phía 0.

Dịch chuyển luận lý

Trong dịch chuyển luận lý, các số 0 sẽ được dịch chuyển vào để thay thế các bit bị loại bỏ. Do đó dịch chuyển luận lý và dịch chuyển số học bên trái là hoàn toàn giống nhau.

Tuy nhiên, dịch chuyển luận lý thêm giá trị 0 vào vị trí bit quan trọng nhất, thay vì sao chép bit mang dấu, điều này khá lý tưởng cho các số nhị phân không dấu, trong khi phép dịch chuyển số học sang phải thì lại lý tưởng cho các số nhị phân bù 2 có dấu.

Quay không nhớ

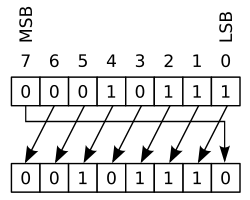Một dạng khác của dịch chuyển được gọi là dịch chuyển vòng hay quay bit. Với phép toán này, các bit được xoay giống như là hai đầu của thanh ghi được gộp lại với nhau. Những giá trị được dịch chuyển vào ở bên phải trong một lần dịch chuyển trái chính là bất kỳ giá trị nào đã được dịch chuyển ra ở bên trái, và ngược lại. Thao tác này hữu ích nếu xảy ra yêu cầu giữ lại toàn bộ bit hiện thời, và thường được sử dụng trong mật mã học kỹ thuật số.

Quay có nhớ

Quay có nhớ tương tự với phép quay không nhớ, nhưng hai đầu của thanh ghi được tách ra bởi cờ nhớ (carry flag). Bit được dịch chuyển vào (ở bất kỳ đầu nào) là giá trị cũ của cờ nhớ, và bit được dịch chuyển ra (ở đầu còn lại) trở thành giá trị mới của cờ nhớ.

Một phép quay có nhớ có thể mô phỏng một phép quay luận lý hoặc số học của một vị trí bằng cách thiết lập cờ nhớ trước tiên. Ví dụ, nếu cờ nhớ mang giá trị 0, thì x XOAY-PHẢI-CÓ-NHỚ-MỘT-LẦN là phép dịch chuyển luận lý sang phải, và nếu cờ nhớ giữ giá trị của bản sao chép của bit chứa dấu, thì x XOAY-PHẢI-CÓ-NHỚ-MỘT-LẦNlà phép dịch chuyển số học sang phải. Vì lý do này, một số vi điều khiển như các PIC tầm thấp chỉ có xoay và xoay có nhớ, mà không cần đến các cấu trúc dịch chuyển số học và luận lý.

Dịch chuyển trong C, C++, C# và Python

Trong các ngôn ngữ dựa trên C, các toán tử dịch chuyển trái và phải lần lượt là << và >>. Số lượng cần dịch chuyển được cung cấp ở đối số thứ hai của toán tử dịch chuyển. Ví dụ:

x = y << 2;

gán cho x kết quả của phép dịch chuyển y sang trái 2 bit, tương đương với phép nhân với 4.

Trong ngôn ngữ C, kết quả của việc dịch chuyển sang phải một giá trị âm là xác định, và giá trị của phép dịch chuyển sang trái của giá trị chứa dấu là không xác định nếu kết quả không được thể hiện dưới dạng của kết quả. Trong C#, phép dịch chuyển sang phải là một phép dịch chuyển số học khi mà toán hạng là biến kiểu int hoặc long. Nếu toán hạng đầu tiên thuộc kiểu uint hoặc ulong, phép dịch chuyển sang phải là phép dịch chuyển luận lý.

Dịch chuyển trong Java

Trong Java, tất cả các giá trị mang kiểu số nguyên đều có dấu, và các toán tử << và >> thực hiện các phép dịch chuyển số học. Java còn thêm vào toán tử >>> để thực hiện phép dịch chuyển luận lý sang phải, nhưng bởi vì phép dịch chuyển sang trái số học và luận lý là như nhau, nên không có toán tử <<< trong Java.

Một vài chi tiết về các toán tử dịch chuyển trong Java:

Thao tác << (dịch trái), >> (dịch phải có dấu), và >>> (dịch phải không dấu) được gọi là các toán tử dịch chuyển.
Kiểu giá trị mà phép dịch bit biểu thị là dạng cao cấp của toán hạng bên trái. Ví dụ, aByte >>> 2 thì tương đương với ((int) aByte) >>> 2.
Nếu như kiểu giá trị cao cấp của toán hạng bên trái là int, thì chỉ có năm bit thấp nhất theo thứ tự của toán hạng bên phải được sử dụng như là khoảng cách dịch chuyển. Điều này giống như là toán hạng bên phải được sử dụng cho một toán tử luận lý thao tác bit AND & với giá trị che đậy 0x1f (0b11111). Khoảng cách dịch chuyển thực ra luôn nằm trong khoảng từ 0 tới 31, một cách bao quát.
Nếu như kiểu giá trị cao cấp của toán hạng bên trái là long, thì chỉ có sáu bit thấp nhất theo tứ tự của toán hạng bên phải được sử dụng như là khoảng cách dịch chuyển. Điều đó giống như là toán hạng bên phải được sử dụng cho một toán tử luận lý thao tác bit AND & với giá trị che đậy 0x3f (0b111111). Khoảng cách dịch chuyển thực ra luôn nằm trong khoảng từ 0 tới 63, một cách bao quát.
Kết quả của n >>> s là n bị dịch chuyển sang phải s bit và đệm 0 vào bên trái tương ứng.
Trong toán tử nói chung và phép dịch bit nói riêng, kiểu dữ liệu byte được hàm ý chuyển thành int. Nếu giá trị byte đó là âm, và bit bậc cao nhất là một, thì các số một sẽ được điền vào để lấp đầy các bytes được thêm vào ở kiểu int. Do đó byte b1=-5; int i = b1 | 0x0200; sẽ cho kết quả i == -5.

Dịch chuyển trong Pascal

Trong Pascal, cũng như các trình biên dịch tương tự nó (như là Object Pascal và Standard Pascal), các thao tác dịch trái và dịch phải lần lượt là shl và shr. Khoảng cách dịch chuyển sẽ được thêm vào trong đối số thứ hai. Ví dụ, câu lệnh sau cho x là kết quả của phép dịch y sang trái hai bit:

x:= y shl 2;

Ứng dụng

Các phép toán trên thao tác bit là đặc biệt cần thiết trong các ngôn ngữ lập trình bậc thấp như các ngôn ngữ dùng để viết ra các trình cắm thiết bị (drivers), đồ họa bậc thấp, hình thành gói giao thức các truyền thông, và giải mã.

Mặc dù các hệ thống máy thường có sẵn các cấu trúc (instructions) hiệu quả cho việc thực hiện các phép toán học và phép luận lý (logic), tuy nhiên trong thực tế, các thao thác này có thể được thực hiện bằng cách kết hợp các toán tử thao tác bit và phép thử số 0 (zero-testing) bằng nhiều cách khác nhau. Ví dụ, dưới đây là mã giải (pseudocode) của phép nhân Ai Cập cổ đại chỉ ra cách để có thể nhân hai số nguyên tùy thích a và b (trong đó a lớn hơn b) mà chỉ cần sử dụng thao tác dịch chuyển bit và phép cộng:

c = 0

while b ≠ 0
  if (b and 1) ≠ 0
    c = c + a
  left shift a by 1
  right shift b by 1

return c

Một ví dụ nữa là mã giải của phép cộng, chỉ ra cách để tính tổng của hai số nguyên a và b sử dụng các toán tử thao tác bit và phép thử số 0:

while a ≠ 0
  c = b and a
  b = b xor a
  left shift c by 1
  a = c

return b

Lưu ý: các dấu = trong các ví dụ trên là phép gán chứ không phải là phép tương đương.

Xem thêm

Bìa Karnaugh