Siêu quần thể

Quần thể 1 được coi là nguồn, từ đó tách biệt thành 1a, 1b và 1c là các quần thể "con". Bốn quần thể này tồn tại cách biệt nhau trong các vùng biển khác nhau, nhưng giữa chúng luôn có di cư và nhập cư. Điều này làm cho nhà khoa học đánh giá rằng đây là "quần thể 4 trong 1", tức siêu quần thể.

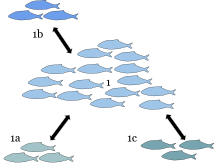
Trong sinh học, siêu quần thể là một nhóm các quần thể cùng loài, tồn tại riêng biệt về không gian nhưng có tương tác chặt chẽ với nhau qua di cư và nhập cư thường xuyên.^[1][2]

Thuật ngữ này được dịch từ nguyên gốc tiếng Anh "metapopulation" do Richard Levins đưa ra vào năm 1969 để mô tả mô hình động lực học của côn trùng gây hại trong nông nghiệp. Sau đó, thuật ngữ được áp dụng rộng rãi trong sinh học, nhất là trong các nghiên cứu sinh học quần thể về các loài trong môi trường sống bị phân mảnh một cách tự nhiên hoặc nhân tạo. Theo cách nói của R. Levins, thì một siêu quần thể là "một quần thể của các quần thể", mà không phải là quần thể siêu lớn (superpopulation) gồm các quần thể nhỏ hơn gọi là quần thể phụ (subpopulations) là các quần thể độc lập tách biệt (isolated populations).^[3][4]

Sau Levins, thì nhà sinh vật học người Phần Lan Ilkka Hanski ở trường Đại học Helsinki là người đóng góp quan trọng cho lý thuyết siêu quần thể.^[5]

Từ xa xưa, nhờ Leonhard Euler, Thomas Malthus và một số nhà khoa học khác, một trong những cách biểu diễn kích thước N của mỗi quần thể độc lập ở tự nhiên là phương trình đơn giản gọi là phương trình BIDE (/baɪd/):

N = B + I - D - E;

trong đó: N = số cá thể của quần thể, B = birth (sinh), I = immigrant (nhập cư), D = death (chết) và E = emigrant (di cư).

Cách biểu diễn này dùng để mô tả quần thể về mặt hình học (geometric populations), đã được giới thiệu ở chương trinh sinh học phổ thông.^[6] Sau đó, các nhà nghiên cứu nhận thấy rằng kích thước quần thể sinh vật trong thực tế phức tạp hơn mô hình trên rất nhiều, cần phải mô tả dựa trên động học quần thể (population dynamics) thì mới phù hợp hơn.

Mô hình Levins

Mô hình ban đầu của Levins được áp dụng cho một siêu quần thể phân bố trên nhiều vùng ở môi trường sống.

Gọi N là kích thước mỗi quần thể ở một vùng tại một thời điểm nhất định. Trong thời gian dt, mỗi vùng có thể trở nên không có cá thể nào do di cư hay tuyệt chủng với xác suất edt. Biểu thức (1 - N) tham chiếu số vùng không có cá thể. Giả sử tốc độ tạo dòng gen c luôn không đổi từ mỗi trong số N vùng, trong thời gian dt. Do đó, tốc độ thay đổi thời gian của các vùng dN / dt, là

${\displaystyle {\frac {dN}{dt}}=cN(1-N)-eN.\,}$

Phương trình này tương đương về mặt toán học với mô hình logistic, khi K là

${\displaystyle K=1-{\frac {e}{c}}\,}$

còn tốc độ tăng trưởng là r

${\displaystyle r=c-e.\,}$

Vậy, ở trạng thái cân bằng, một số phần trong môi trường sống của loài sẽ luôn không có cá thể nào chiếm giữ.

Nguồn trích dẫn

1. John N. Thompson. “Metapopulation (ECOLOGY)”.
2. Paulina M. “Metapopulation: Definition, Theory & Examples”.
3. Levins, R. (1969), “Some demographic and genetic consequences of environmental heterogeneity for biological control”, Bulletin of the Entomological Society of America, 15 (3): 237–240, doi:10.1093/besa/15.3.237
4. “Metapopulations”. Bản gốc lưu trữ ngày 9 tháng 7 năm 2019.
5. JEF AKST. “Population Ecologist Dies”.
6. "Sinh học 12" - Nhà xuất bản Giáo dục, 2019

Liên kết ngoài

• Helsinki-science: Metapopulation