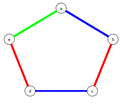
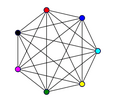
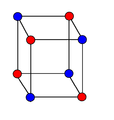
Tô màu đồ thị

Đồ thị Petersen có sắc số bằng 3.

Trong Lý thuyết đồ thị, tô màu đồ thị (tiếng Anh: graph coloring) là trường hợp đặc biệt của gán nhãn đồ thị, mà trong đó mỗi đỉnh hay mỗi cạnh hay mỗi miền của đồ thị có thể được gán bởi một màu hay một tập hợp các màu nào đó. Tô màu đồ thị có thể là:

• tô màu đỉnh (tiếng Anh: vertex coloring) là gán cho mỗi đỉnh của đồ thị một màu nào đó sao cho không có hai đỉnh nào liền kề lại trùng màu nhau;
• tô màu cạnh (tiếng Anh: edge coloring) là gán cho mỗi cạnh của đồ thị một màu nào đó sao cho sao cho không có 2 cạnh nào trùng màu;
• tô màu miền (tiếng Anh: face coloring) là gán cho mỗi miền của đồ thị phẳng một màu sao cho không có 2 miền có chung đường biên lại cùng màu.

Sắc số (tiếng Anh: chromatic number) của một đồ thị là số màu ít nhất để tô các đỉnh. Sắc số của đồ thị G được ký hiệu là χ(G).

Số màu cạnh (tiếng Anh: chromatic index) của một đồ thị là số màu ít nhất dùng để tô các cạnh. Số màu cạnh của đồ thị G được ký hiệu là χ'(G).

Số màu cạnh của đồ thị G bất kì bằng sắc số của đồ thị đường L((G)) của đồ thị đó:

χ'(G) = χ(L(G)),

do đó việc nghiên cứu tô màu cạnh của G tương đương với nghiên cứu tô màu đỉnh của L(G).

Các định lý và tính chất

Các giá trị giới hạn của sắc số

Rõ ràng sắc số của một đồ thị sẽ không vượt quá số đỉnh của nó (bậc của đồ thị):

${\displaystyle 1\leq \chi (G)\leq n.\,}$.

Nếu G có clique kích thước k thì cần ít nhất k màu để tô màu đỉnh cho clique này (xem thêm bài về đồ thị đầy đủ), như vậy sắc số của một đồ thị sẽ không nhỏ hơn chỉ số clique của đồ thị đó:

${\displaystyle \chi (G)\geq \omega (G).\,}$

Nếu đồ thị đơn G có bậc cực đại bằng Δ(G) thì sắc số của nó không vượt quá Δ(G)+1^[1].

Chứng minh

Gọi số đỉnh của G là n.

Ta dùng Δ(G)+1 màu để tô n đỉnh của G như sau: xuất phát từ đỉnh thứ nhất đến đỉnh thứ n, tô màu đỉnh đầu tiên bằng 1 màu tùy ý trong Δ(G)+1 màu. Tô màu đỉnh kế tiếp bằng một màu khác với các màu đã tô cho các láng giềng của đỉnh đó. Việc tô màu này luôn thực hiện được, đến lượt 1 đỉnh bất kì, ta luôn có màu để tô cho nó, vì số màu Δ(G)+1 lớn hơn bậc của đỉnh bất kì.

Tổng quát hơn là định lý Brook, định lý khẳng định rằng:

Tất cả mọi đồ thị đơn và liên thông G, ngoại trừ đồ thị đầy đủ ${\displaystyle K_{n}}$ và đồ thị chu trình bậc lẻ ${\displaystyle W_{n}}$, đều có sắc số nhỏ hơn hoặc bằng bậc cực đại:

${\displaystyle \chi (G)\leq }$ Δ(G).

Nếu đồ thị G có m cạnh thì sắc số của nó thỏa mãn:

${\displaystyle \chi (G)(\chi (G)-1)\leq 2m.\,}$

Chứng minh

Chứng minh quy nạp theo m (m là số tự nhiên) mệnh đề (*) sau:

nếu đồ thị G có không quá m cạnh thì sắc số của nó thỏa mãn:

${\displaystyle \chi (G)(\chi (G)-1)\leq 2m.\,}$

Với m=0,1, mệnh đề (*) đúng.

Giả sử mệnh đề (*) đúng đến m-1. Xét m.

Gọi ${\displaystyle \chi }$ là số tự nhiên lớn nhất thỏa mãn:

${\displaystyle \chi (\chi -1)\leq 2m.\,}$

Nếu bậc cực đại của G nhỏ hơn ${\displaystyle \chi }$ thì như ta đã biết, sắc số của G không vượt quá bậc cực đại của nó cộng với một, nên sẽ không vượt quá ${\displaystyle \chi }$, suy ra luôn điều phải chứng minh.

Nếu bậc cực đại của G lớn hơn hoặc bằng ${\displaystyle \chi }$, suy ra trong G tồn tại đỉnh a có deg(a) lớn hơn hoặc bằng ${\displaystyle \chi }$.

Xóa đỉnh a và các cạnh liên thuộc của nó khỏi G ta nhận được đồ thị mới là G', đồ thị này có số cạnh thỏa mãn:

${\displaystyle m'=m-deg(a)\leq m-\chi }$

Theo giả thiết quy nạp, mệnh đề (*) đúng cho m' nên:

${\displaystyle \chi (G')\leq 2m'\leq 2(m-\chi )}$,

Suy ra:

${\displaystyle \chi (G')\leq \chi -1}$.

Tức là sắc số của G' không thể vượt quá ${\displaystyle \chi -1}$, từ đó suy ra sắc số của G không vượt quá ${\displaystyle \chi }$. Như vậy mệnh đề cũng đúng với m.

Suy ra mệnh đề (*) đúng với mọi m là số tự nhiên.

Một số định lý liên quan của sắc số

Định lý 1

Bất cứ chu trình độ dài lẻ nào cũng đều có sắc số bằng 3

Chứng minh: Giả sử chu trình có độ dài là ${\displaystyle 2n+1}$ ta chứng minh theo số ${\displaystyle n}$

• ${\displaystyle n=1}$ chu trình gồm 3 đỉnh mà 2 đỉnh bất kì đều kề nhau ${\displaystyle \Rightarrow }$ dùng đúng 3 màu để tô
• ${\displaystyle (n)\Rightarrow (n+1)}$ Giả sử ${\displaystyle \alpha }$ là một chu trình có độ dài ${\displaystyle 2(n+1)+1=2n+3}$ với các dãy đỉnh là ${\displaystyle x_{1}}$, ${\displaystyle x_{2}}$,...,${\displaystyle x_{2n+1}}$,${\displaystyle x_{2n+2}}$,${\displaystyle x_{2n+3}}$.

Nối ${\displaystyle x_{1}}$ với ${\displaystyle x_{2n+1}}$ ta được một chu trình ${\displaystyle \alpha }$'có độ dài ${\displaystyle 2n+1}$.

Theo giả thuyết quy nạp chu trình ${\displaystyle \alpha }$' có sắc số bằng 3.

Lấy màu của ${\displaystyle x_{1}}$ tô cho ${\displaystyle x_{2n+2}}$ còn màu của ${\displaystyle x_{2n+1}}$ tô cho ${\displaystyle x_{2n+3}}$.

Chu trình ${\displaystyle \alpha }$ được tô màu mà không thêm màu mới vào.

Vậy chu trình ${\displaystyle \alpha }$ có sắc số bằng 3

Định lý 2

Đồ thị đầy đủ n đỉnh K_n có sắc số bằng n

Một số tiêu chuẩn đơn giản để kiểm tra xem 1 đồ thị có hai sắc số hay không:

• Ta có định lý: Giả sử đồ thị G có ít nhất một cạnh. Đồ thị G có hai sắc số khi và chỉ khi G không có chu trình đơn vô hướng độ dài lẻ.

Chứng minh:

• Giả sử G là đồ thị có hai sắc số. Theo Định lý 1 thì G không thể có chu trình đơn vô hướng độ dài lẻ.
• Ngược lại giả sử G không có chu trình đơn vô hướng độ dài lẻ. Không mất tính tổng quát có thể xem G liên thông.

Chọn 1 đỉnh a nào đó bất kì trong đồ thị

Đặt ${\displaystyle m(a)=0}$ (m: số màu)

Với ${\displaystyle x}$ ${\displaystyle \neq }$ ${\displaystyle a}$ Ta ký hiệu ${\displaystyle d(x)}$là độ dài đường đi vô hướng ngắn nhất nối ${\displaystyle a}$ với${\displaystyle x}$

Đặt ${\displaystyle m(x)=d(x)}$ mod 2

Ta sẽ chứng minh m là hàm màu của G

Giả sử ${\displaystyle x,y}$ kề nhau

Lấy ${\displaystyle d(x)}$ là đường đi vô hướng ngắn nhất nối a với x có độ dài ${\displaystyle d(x)}$

${\displaystyle d(y)}$ là đường đi vô hướng ngắn nhất nối ${\displaystyle a}$ với ${\displaystyle y}$ có độ dài ${\displaystyle d(y)}$

Chu trình đơn ${\displaystyle [d(x),(x,y),d(y)]}$ có độ dài ${\displaystyle d(x)+d(y)+1}$phải là một số chẵn

Vậy thì ${\displaystyle d(x)+d(y)}$ là một số lẻ ${\displaystyle \Rightarrow }$ ${\displaystyle d(x),d(y)}$ khác nhau tính chẵn lẻ

${\displaystyle \Rightarrow }$${\displaystyle m(x)}$ ${\displaystyle \neq }$ ${\displaystyle m(y)}$

Hàm tô màu m có hai giá trị, vậy sắc số ≤ 2. G có ít nhất một cạnh nên sắc số của nó bằng 2

Từ định lý trên ta có hệ quả sau: Tất cả các chu trình độ dài chẵn đều có sắc số bằng 2.

Định lý 3

Ví dụ định lý 3: Tìm sắc số đồ thị

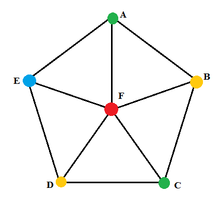
Phát biểu: Nếu G có chứa 1 đồ thị con đẳng cấu với K_n thì ${\displaystyle x(G)\geq n}$.

Chứng minh: Hiển nhiên

Các giá trị giới hạn của số màu cạnh

Định lý 1

Số màu cạnh của đồ thị đơn G bất kì không vượt quá số đỉnh của nó.

Chứng minh

Xét đồ thị ${\displaystyle K'_{n}}$ có hai đỉnh bất kì liền kề và ${\displaystyle K'_{n}}$ có các khuyên. n là số đỉnh của ${\displaystyle K'_{n}}$.

Đánh số các đỉnh của ${\displaystyle K'_{n}}$ là ${\displaystyle v_{1},v_{2},v_{3},\ldots ,v_{n}}$.

Chỉ cần chứng minh ${\displaystyle K'_{n}}$ có thể tô màu các cạnh bởi n màu thì suy ra đồ thị đơn G bất kì có số đỉnh không vượt quá n đều có thể tô các cạnh bởi n màu.

Ký hiệu các màu là ${\displaystyle M_{1},M_{2},\ldots ,M_{n}}$.

Khi đó ta có cách tô màu cho ${\displaystyle K'_{n}}$ như sau.

Ma trận dưới đây biểu thị cách tô màu, trong đó:

• giá trị ở hàng thứ i cột j chính là màu được gán cho cạnh ${\displaystyle (v_{i},v_{j})}$;

${\displaystyle {\begin{matrix}&v_{1}&v_{2}&v_{3}&v_{4}&\cdots &v_{n-2}&v_{n-1}&v_{n}\\v_{1}&M_{1}&M_{2}&M_{3}&M_{4}&\cdots &M_{n-2}&M_{n-1}&M_{n}\\v_{2}&M_{2}&M_{3}&M_{4}&M_{5}&\cdots &M_{n-1}&M_{n}&M_{1}\\v_{3}&M_{3}&M_{4}&M_{5}&M_{6}&\cdots &M_{n}&M_{1}&M_{2}\\v_{4}&M_{4}&M_{5}&M_{6}&M_{7}&\cdots &M_{1}&M_{2}&M_{3}\\\vdots &\vdots &\vdots &\vdots &\vdots &\ddots &\vdots &\vdots &\vdots &\\v_{n}&M_{n}&M_{1}&M_{2}&M_{3}&\cdots &M_{n-3}&M_{n-2}&M_{n-1}\end{matrix}}.}$

Định lý König khẳng định rằng đối với đồ thị hai phía G, số màu cạnh của nó bằng bậc cực đại của nó: ${\displaystyle \chi '(G)=\Delta (G)}$.

Định lý Vizing khẳng định rằng, nếu đồ thị đơn G có bậc cực đại bằng ${\displaystyle \Delta (G)}$ thì số màu cạnh của nó bằng ${\displaystyle \Delta (G)}$ hoặc ${\displaystyle \Delta (G)+1}$.

Đa thức màu

Xem bài đa thức màu.

Sắc số và số màu cạnh của một số đồ thị cơ bản

Khái niệm sắc số liên quan đến bài toán tô màu như sau: Hãy tô màu các đỉnh của đồ thị đã cho, sao cho 2 đỉnh kề phải được tô bằng hai màu khác nhau

Đồ thị hai phía

• 
  Các đỉnh của đồ thị ${\displaystyle K_{3,3}}$ được tô bằng hai màu xanh và đỏ.

Đồ thị hai phía đầy đủ ${\displaystyle K_{m,n}}$ có sắc số bằng 2: χ(${\displaystyle K_{3,3}}$)=2. Mở rộng: một đồ thị hai phía bất kì có sắc số không vượt quá 2.

Ví dụ minh họa là các đỉnh của đồ thị ${\displaystyle K_{3,3}}$ có thể được tô bởi hai màu xanh và đỏ.

Đồ thị chu trình

• 
  Các đỉnh của đồ thị ${\displaystyle C_{5}}$ tô được bởi ít nhất 3 màu.
• 
  Các đỉnh của đồ thị ${\displaystyle C_{6}}$ tô được bởi ít nhất 2 màu.
• 
  Các cạnh của đồ thị ${\displaystyle C_{5}}$ tô được bởi ít nhất 3 màu.
• 
  Các cạnh của đồ thị ${\displaystyle C_{6}}$ tô được bởi ít nhất 2 màu.

Đồ thị chu trình ${\displaystyle C_{n}}$ có sắc số bằng:

• χ(${\displaystyle C_{n}}$)= 3, nếu n lẻ.
• χ(${\displaystyle C_{n}}$)= 2, nếu n chẵn.

Số màu cạnh:

• χ'(${\displaystyle C_{n}}$)= 3, nếu n lẻ.
• χ'(${\displaystyle C_{n}}$)= 2, nếu n chẵn.

Đồ thị bánh xe

• 
  Các đỉnh của đồ thị ${\displaystyle W_{6}}$ tô được bởi ít nhất 4 màu.
• 
  Các đỉnh của đồ thị ${\displaystyle W_{7}}$ tô được bởi ít nhất 3 màu.
• 
  Các cạnh của đồ thị ${\displaystyle W_{7}}$ tô được bởi ít nhất 6 màu.

Đồ thị bánh xe ${\displaystyle W_{n}}$ (n≥4) có sắc số bằng:

• χ(${\displaystyle W_{n}}$)= 3, nếu n lẻ.
• χ(${\displaystyle W_{n}}$)= 4, nếu n chẵn.

Số màu cạnh (n≥3):

• χ'(${\displaystyle W_{n}}$)= n-1.

Đồ thị đầy đủ

• 
  Đồ thị đầy đủ 7 đỉnh có sắc số bằng 7.
• 
  ${\displaystyle K_{5}}$ có số màu cạnh bằng 5.
• 
  ${\displaystyle K_{4}}$ có số màu cạnh bằng 3.

Đồ thị đầy đủ ${\displaystyle K_{n}}$ có sắc số bằng:

• χ(${\displaystyle K_{n}}$) = n.

Số màu cạnh:

• χ'(${\displaystyle K_{n}}$) = n, nếu n lẻ.
• χ'(${\displaystyle K_{n}}$) = n-1, nếu n chẵn.

Chứng minh

Đánh số các đỉnh của ${\displaystyle K_{n}}$ là ${\displaystyle v_{1},v_{2},v_{3},\ldots ,v_{n}}$.

Do mỗi đỉnh của ${\displaystyle K_{n}}$ có bậc bằng n-1, nên số màu cạnh của nó không nhỏ hơn n-1, do đó χ'(${\displaystyle K_{n}}$) bằng n hoặc n-1.

Chứng minh χ'(${\displaystyle K_{n}}$)=n-1 với n chẵn:

Ta chỉ cần chỉ ra cách tô n-1 màu cho các cạnh của ${\displaystyle K_{n}}$ là được.

Ký hiệu các màu là ${\displaystyle M_{1},M_{2},\ldots ,M_{n-1}}$.

Ma trận dưới đây biểu thị cách tô màu, trong đó:

• giá trị ở hàng thứ i cột j chính là màu được gán cho cạnh ${\displaystyle (v_{i},v_{j})}$;
• X nghĩa là không được gán màu.

${\displaystyle {\begin{matrix}&v_{1}&v_{2}&v_{3}&v_{4}&\cdots &v_{n-2}&v_{n-1}&v_{n}\\v_{1}&X&M_{1}&M_{2}&M_{3}&\cdots &M_{n-3}&M_{n-2}&M_{n-1}\\v_{2}&M_{1}&X&M_{3}&M_{4}&\cdots &M_{n-2}&M_{n-1}&M_{2}\\v_{3}&M_{2}&M_{3}&X&M_{5}&\cdots &M_{n-1}&M_{1}&M_{4}\\v_{4}&M_{3}&M_{4}&M_{5}&X&\cdots &M_{1}&M_{2}&M_{6}\\\vdots &\vdots &\vdots &\vdots &\vdots &\ddots &\vdots &\vdots &\vdots &\\v_{n}&M_{n-1}&M_{2}&M_{4}&M_{6}&\cdots &\cdots &\cdots &X\end{matrix}}.}$

Ví dụ với n=6, ta có cách tô màu như sau:

${\displaystyle {\begin{matrix}&v_{1}&v_{2}&v_{3}&v_{4}&v_{5}&v_{6}\\v_{1}&X&M_{1}&M_{2}&M_{3}&M_{4}&M_{5}\\v_{2}&M_{1}&X&M_{3}&M_{4}&M_{5}&M_{2}\\v_{3}&M_{2}&M_{3}&X&M_{5}&M_{1}&M_{4}\\v_{4}&M_{3}&M_{4}&M_{5}&X&M_{2}&M_{1}\\v_{5}&M_{4}&M_{5}&M_{1}&M_{2}&X&M_{3}\\v_{6}&M_{5}&M_{2}&M_{4}&M_{1}&M_{3}&X\\\end{matrix}}}$

Chứng minh χ'(${\displaystyle K_{n}}$)=n với n lẻ:

Trái lại, giả sử tồn tại n lẻ sao cho χ'(${\displaystyle K_{n}}$) = n-1.

Xét màu M bất kì, các cạnh tô màu M ký hiệu là ${\displaystyle (v_{i_{1}},v_{j_{1}}),(v_{i_{2}},v_{j_{2}}),\ldots ,(v_{i_{k}},v_{j_{k}})}$, trong đó ${\displaystyle v_{i_{1}},v_{j_{1}},v_{i_{2}},v_{j_{2}},\ldots ,v_{i_{k}},v_{j_{k}}}$ là các đầu mút đôi một phân biệt. Như vậy có 2k đỉnh có cạnh liên thuộc tô bởi màu M, mà n lẻ nên tồn tại ít nhất một đỉnh ${\displaystyle v_{i}}$ nào đó không có cạnh liên thuộc tô bởi màu M. Như vậy các cạnh liên thuộc với đỉnh ${\displaystyle v_{i}}$ chỉ được tô bởi không quá n-2 màu, mà ${\displaystyle deg(a)=n-1}$ (vô lý).

Đồ thị siêu khối

• 
  Sắc số của ${\displaystyle Q_{2}}$ bằng 2.
• 
  Sắc số của ${\displaystyle Q_{3}}$ bằng 2.

Đồ thị siêu khối ${\displaystyle Q_{n}}$ có sắc số bằng 2, vì bản thân nó là đồ thị phân đôi.

Ứng dụng

Tô màu bản đồ

Trên các bản đồ, các miền khác nhau (miền ở đây được hiểu là các quốc gia trên bản đồ thế giới hay các tỉnh trong một bản đồ hành chính quốc gia) được tô màu sao cho 2 miền có chung biên giới không trùng màu nhau. Đối với bản đồ có nhiều miền, nếu ta dùng một số lượng lớn màu thì sẽ rất khó phân biệt các miền có màu gần giống nhau, vì thế người ta chỉ dùng một số lượng màu nhất định để tô màu bản đồ. Một bài toán được đặt ra là: có thể dùng ít nhất bao nhiêu màu để tô màu một bản đồ sao cho các miền kề nhau không cùng một màu^[2] (tr.593).

Bài toán này dẫn đến định lý bốn màu nổi tiếng và định lý năm màu^[3]. Các dạng bài toán tô màu bản đồ có thể áp dụng Thuật toán tô màu Greedy để tìm ra số màu ít nhất để tô cho các miền trên bản đồ.

Xem thêm

• Định lý bốn màu
• Đa thức màu
• Thuật toán tô màu Greedy

Chú thích

1. Vũ Đình Hòa, Đồ thị, Nhà xuất bản Giáo dục
2. Kenneth H.Rosen, Toán học rời rạc, Nhà xuất bản Khoa Học và Kỹ thuật Hà Nội, 2003
3. Trần Đan Thư - Dương Anh Đức (2008). Lý Thuyết Đồ Thị. Nhà xuất bản Đại học Quốc gia TP Hồ Chí Minh.

Tham khảo

• Barenboim, L.; Elkin, M. (2009), "Distributed (Δ + 1)-coloring in linear (in Δ) time", Proceedings of the 41st Symposium on Theory of Computing, tr. 111–120, doi:10.1145/1536414.1536432, ISBN 978-1-60558-506-2

• Panconesi, A.; Srinivasan, A. (1996), "On the complexity of distributed network decomposition", Journal of Algorithms, quyển 20

• Schneider, J. (2010), "A new technique for distributed symmetry breaking", Proceedings of the [[Symposium on Principles of Distributed Computing]] (PDF), Bản gốc (PDF) lưu trữ ngày 30 tháng 7 năm 2013, truy cập ngày 17 tháng 7 năm 2012 {{Chú thích}}: Tựa đề URL chứa liên kết wiki (trợ giúp)
• Schneider, J. (2008), "A log-star distributed maximal independent set algorithm for growth-bounded graphs", Proceedings of the [[Symposium on Principles of Distributed Computing]] (PDF), Bản gốc (PDF) lưu trữ ngày 30 tháng 7 năm 2013, truy cập ngày 17 tháng 7 năm 2012 {{Chú thích}}: Tựa đề URL chứa liên kết wiki (trợ giúp)

• Beigel, R.; Eppstein, D. (2005), "3-coloring in time O(1.3289ⁿ)", Journal of Algorithms, 54 (2)): 168–204, doi:10.1016/j.jalgor.2004.06.008
• Björklund, A.; Husfeldt, T.; Koivisto, M. (2009), "Set partitioning via inclusion–exclusion", SIAM Journal on Computing, 39 (2): 546–563, doi:10.1137/070683933
• Brèlaz, D. (1979), "New methods to color the vertices of a graph", Communications of the ACM, 22 (4): 251–256, doi:10.1145/359094.359101
• Brooks, R. L.; Tutte, W. T. (1941), "On colouring the nodes of a network", Proceedings of the Cambridge Philosophical Society, 37 (2): 194–197, doi:10.1017/S030500410002168X
• de Bruijn, N. G.; Erdős, P. (1951), "A colour problem for infinite graphs and a problem in the theory of relations" (PDF), Nederl. Akad. Wetensch. Proc. Ser. A, 54: 371–373 (= Indag. Math. 13)
• Byskov, J.M. (2004), "Enumerating maximal independent sets with applications to graph colouring", Operations Research Letters, 32 (6): 547–556, doi:10.1016/j.orl.2004.03.002

• Chaitin, G. J. (1982), "Register allocation & spilling via graph colouring", Proc. 1982 SIGPLAN Symposium on Compiler Construction, tr. 98–105, doi:10.1145/800230.806984, ISBN 0-89791-074-5
• Cole, R.; Vishkin, U. (1986), "Deterministic coin tossing with applications to optimal parallel list ranking", Information and Control, 70 (1): 32–53, doi:10.1016/S0019-9958(86)80023-7
• Cormen, T. H.; Leiserson, C. E.; Rivest, R. L. (1990), Introduction to Algorithms (ấn bản thứ 1), The MIT Press
• Dailey, D. P. (1980), "Uniqueness of colorability and colorability of planar 4-regular graphs are NP-complete", Discrete Mathematics, 30 (3): 289–293, doi:10.1016/0012-365X(80)90236-8
• Duffy, K.; O'Connell, N.; Sapozhnikov, A. (2008), "Complexity analysis of a decentralised graph colouring algorithm" (PDF), Information Processing Letters, 107 (2): 60–63, doi:10.1016/j.ipl.2008.01.002
• Fawcett, B. W. (1978), "On infinite full colourings of graphs", Can. J. Math., XXX: 455–457
• Garey, M. R.; Johnson, D. S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0-7167-1045-5
• Garey, M. R.; Johnson, D. S.; Stockmeyer, L. (1974), "Some simplified NP-complete problems", Proceedings of the Sixth Annual ACM Symposium on Theory of Computing, tr. 47–63, doi:10.1145/800119.803884
• Goldberg, L. A.; Jerrum, M. (tháng 7 năm 2008), "Inapproximability of the Tutte polynomial", Information and Computation, 206 (7): 908–929, doi:10.1016/j.ic.2008.04.003
• Goldberg, A. V.; Plotkin, S. A.; Shannon, G. E. (1988), "Parallel symmetry-breaking in sparse graphs", SIAM Journal on Discrete Mathematics, 1 (4): 434–446, doi:10.1137/0401044
• Guruswami, V.; Khanna, S. (2000), "On the hardness of 4-coloring a 3-colorable graph", Proceedings of the 15th Annual IEEE Conference on Computational Complexity, tr. 188–197, doi:10.1109/CCC.2000.856749, ISBN 0-7695-0674-7
• Halldórsson, M. M. (1993), "A still better performance guarantee for approximate graph coloring", Information Processing Letters, 45: 19–23, doi:10.1016/0020-0190(93)90246-6
• Holyer, I. (1981), "The NP-completeness of edge-coloring", SIAM Journal on Computing, 10 (4): 718–720, doi:10.1137/0210055
• Crescenzi, P.; Kann, V. (tháng 12 năm 1998), "How to find the best approximation results — a follow-up to Garey and Johnson", ACM SIGACT News, 29 (4): 90, doi:10.1145/306198.306210
• Jaeger, F.; Vertigan, D. L.; Welsh, D. J. A. (1990), "On the computational complexity of the Jones and Tutte polynomials", Mathematical Proceedings of the Cambridge Philosophical Society, 108: 35–53, doi:10.1017/S0305004100068936
• Jensen, T. R.; Toft, B. (1995), Graph Coloring Problems, Wiley-Interscience, New York, ISBN 0-471-02865-7
• Khot, S. (2001), "Improved inapproximability results for MaxClique, chromatic number and approximate graph coloring", Proc. 42nd Annual Symposium on Foundations of Computer Science, tr. 600–609, doi:10.1109/SFCS.2001.959936, ISBN 0-7695-1116-3
• Kubale, M. (2004), Graph Colorings, American Mathematical Society, ISBN 0-8218-3458-4
• Kuhn, F. (2009), "Weak graph colorings: distributed algorithms and applications", Proceedings of the 21st Symposium on Parallelism in Algorithms and Architectures, tr. 138–144, doi:10.1145/1583991.1584032, ISBN 978-1-60558-606-9
• Lawler, E.L. (1976), "A note on the complexity of the chromatic number problem", Information Processing Letters, 5 (3): 66–67, doi:10.1016/0020-0190(76)90065-X

• Leith, D.J.; Clifford, P. (2006), "A Self-Managed Distributed Channel Selection Algorithm for WLAN", Proc. RAWNET 2006, Boston, MA (PDF)
• Linial, N. (1992), "Locality in distributed graph algorithms", SIAM Journal on Computing, 21 (1): 193–201, doi:10.1137/0221015
• van Lint, J. H.; Wilson, R. M. (2001), A Course in Combinatorics (ấn bản thứ 2), Cambridge University Press, ISBN 0-521-80340-3. {{Chú thích}}: Kiểm tra giá trị |isbn=: ký tự không hợp lệ (trợ giúp)
• Marx, Dániel (2004), "Graph colouring problems and their applications in scheduling", Periodica Polytechnica, Electrical Engineering, quyển 48, tr. 11–16, CiteSeer^x: 10.1.1.95.4268
• Mycielski, J. (1955), "Sur le coloriage des graphes" (PDF), Colloq. Math., 3: 161–162.
• Panconesi, Alessandro; Rizzi, Romeo (2001), "Some simple distributed algorithms for sparse networks", Distributed Computing, 14 (2), Berlin, New York: Springer-Verlag: 97–100, doi:10.1007/PL00008932, ISSN 0178-2770
• Sekine, K.; Imai, H.; Tani, S. (1995), "Computing the Tutte polynomial of a graph of moderate size", Proc. 6th International Symposium on Algorithms and Computation (ISAAC 1995), Lecture Notes in Computer Science, quyển 1004, Springer, tr. 224–233, doi:10.1007/BFb0015427, ISBN 3-540-60573-8
• Welsh, D. J. A.; Powell, M. B. (1967), "An upper bound for the chromatic number of a graph and its application to timetabling problems", The Computer Journal, 10 (1): 85–86, doi:10.1093/comjnl/10.1.85
• West, D. B. (1996), Introduction to Graph Theory, Prentice-Hall, ISBN 0-13-227828-6
• Wilf, H. S. (1986), Algorithms and Complexity, Prentice–Hall
• Zuckerman, D. (2007), "Linear degree extractors and the inapproximability of Max Clique and Chromatic Number", Theory of Computing, 3: 103–128, doi:10.4086/toc.2007.v003a006
• Zykov, A. A. (1949), "О некоторых свойствах линейных комплексов (On some properties of linear complexes)", Math. Sbornik. (bằng tiếng Nga), 24(66) (2): 163–188
• Jensen, Tommy R.; Toft, Bjarne (1995), Graph Coloring Problems, John Wiley & Sons, ISBN 0-471-02865-7, 9780471028659 {{Chú thích}}: Kiểm tra giá trị |isbn=: ký tự không hợp lệ (trợ giúp)

Liên kết ngoài

• Graph Coloring Page Lưu trữ ngày 12 tháng 4 năm 2008 tại Wayback Machine by Joseph Culberson (graph coloring programs)
• CoLoRaTiOn by Jim Andrews and Mike Fellows is a graph coloring puzzle
• Links to Graph Coloring source codes Lưu trữ ngày 4 tháng 7 năm 2008 tại Wayback Machine
• Code for efficiently computing Tutte, Chromatic and Flow Polynomials Lưu trữ ngày 16 tháng 4 năm 2008 tại Wayback Machine by Gary Haggard, David J. Pearce and Gordon Royle
• Graph Coloring Web Application Lưu trữ ngày 22 tháng 6 năm 2012 tại Wayback Machine