Tọa độ tỉ cự

Trong hình học, hệ tọa độ Barycentric (Còn gọi là Hệ tọa độ tỉ cự) là một hệ tọa độ trong đó vị trí của một điểm trong một đa diện, được xác định là một trọng tâm hay tâm tỉ cự. Tọa độ cũng được mở rộng bên ngoài đa diện, nơi có một hoặc nhiều tọa độ có giá trị âm. Khái niệm này được giới thiệu bởi August Ferdinand Mobius (1827).

Định nghĩa

Cho ${\displaystyle x_{1},...,x_{n}}$ là một hệ điểm trên một đa diện của không gian afin A (affine space). Nếu một điểm p thuộc A,

${\displaystyle {\text{p}}\sum _{i=1}^{n}a_{i}=\sum _{i=1}^{n}a_{i}x_{i}}$ hay ${\displaystyle (a_{1}+a_{2}+\cdots +a_{n}){\text{p}}=a_{1}x_{1}+a_{2}x_{2}+\cdots +a_{n}x_{n}}$

và có ít nhất một trong ${\displaystyle a_{1},\dots ,a_{n}}$ không bị triệt tiêu nên ta nói rằng dãy các hệ số ${\displaystyle \left(a_{1},a_{2},\dots ,a_{n}\right)}$ là một tọa độ Barycentric của p có mối quan hệ với dãy ${\displaystyle x_{1},\ldots ,x_{n}.}$ Bản thân các đỉnh của chúng có tọa độ ${\displaystyle x_{1}=(1,0,0,...,0),x_{2}=(0,1,0,...,0),x_{n}=(0,0,...,1).}$ Các tọa barycentric không phải là duy nhất: với mọi b khác 0, ${\displaystyle ba_{1},...ba_{n}}$ cũng là tọa độ barycentric của p. Nếu tọa độ không âm, p nằm trong bao lồi của ${\displaystyle x_{1},...,x_{n}}$, vậy trong một đa diện, điểm của nó được xem như là một đỉnh.

Theo định nghĩa, tọa độ barycentric được biểu diễn dưới dạng tọa độ đồng nhất. Đôi khi giá trị của tọa độ bị hạn chế bởi một điều kiện

${\displaystyle \sum a_{i}=1}$

làm cho các tọa độ đó là duy nhất, cho nên chúng là tọa độ afin (affine coordinates).

Tọa độ barycentric trên một tam giác

Các tọa độ barycentric ${\displaystyle (\lambda _{1},\lambda _{2},\lambda _{3})}$ trong tam giác đều và tam giác vuông.

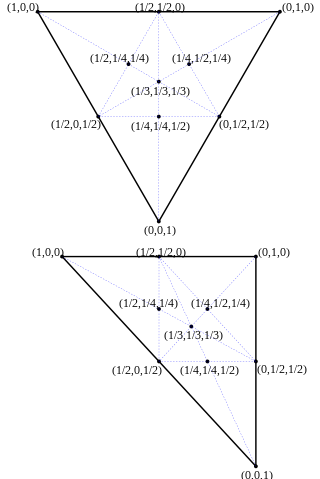
Trong tam giác, tọa độ barycentric có thể được nói với tên gọi khác là tọa độ của một bề mặt, vì tọa độ của P liên hệ đến các tam giác PBC, PCA và PAB trong tam giác lớn nhất ABC. Tọa độ barycentric là một công cụ rất quan trọng trong các ứng dụng kỹ thuật liên quan đến tam giác bao gồm miền con của tam giác. Nó cho thấy việc phân tích và tính toán một bài toán trở nên dễ dàng và các bảng tứ phương Gauss được trình bày trong đó có các tọa độ barycentric. Xét một tam giác ${\displaystyle T}$ cấu thành bởi 3 đỉnh r₁, r₂ và r₃. Với mỗi điểm đó ta có thể viết một tổ hợp lồi của 3 điểm. Nói cách khác, với mỗi điểm r ta có thứ tự duy nhất các số ${\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}\geq 0}$ vậy nên ${\displaystyle \lambda _{1}+\lambda _{2}+\lambda _{3}=1}$ và

${\displaystyle r=\lambda _{1}r_{1}+\lambda _{2}r_{2}+\lambda _{3}r_{3}.}$

3 số ${\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}}$ chỉ ra rằng tọa độ của điểm r liên hệ với tam giác. Nó có thể được ký hiệu dưới dạng ${\displaystyle \alpha ,\beta ,\gamma .}$ Chú ý rằng mặc dù nó có 3 tọa độ nhưng nó chỉ có 2 "mức độ tự do", vì ${\displaystyle \lambda _{1}+\lambda _{2}+\lambda _{3}=1.}$

Chuyển đổi giữa tọa độ barycentric và tọa độ Cartesian

Với mỗi điểm r trong một tam giác có thể tìm được tọa độ barycentric ${\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}}$ từ tọa độ Cartesian ${\displaystyle (x,y)}$ và ngược lại.

Ta có thể viết tọa độ Cartesian của điểm r bằng các thành phần Cartesian của một hệ điểm tam giác ${\displaystyle r_{1},r_{2},r_{3}}$ với ${\displaystyle r_{i}=(x_{i},y_{i})}$, về tọa độ r thì ta có

${\displaystyle x=\lambda _{1}x_{1}+\lambda _{2}x_{2}+\lambda _{3}x_{3}}$

${\displaystyle y=\lambda _{1}y_{1}+\lambda _{2}y_{2}+\lambda _{3}x_{3}.}$

Để đổi ngược lại, từ tọa độ Cartesian vào tọa độ barycentric, đầu tiên thế ${\displaystyle \lambda _{3}=1-\lambda _{1}-\lambda _{2}}$ vào hai biểu thức trên để ta có được

${\displaystyle x=\lambda _{1}x_{1}+\lambda _{2}x_{2}+(1-\lambda _{1}-\lambda _{2})x_{3}}$

${\displaystyle y=\lambda _{1}y_{1}+\lambda _{2}y_{2}+(1-\lambda _{1}-\lambda _{2})y_{3}}$

Chuyển vế đổi dấu ta được

${\displaystyle \lambda _{1}(x_{1}-x_{3})+\lambda _{2}(x_{2}-x_{3})+x_{3}-x=0}$

${\displaystyle \lambda _{1}(y_{1}-y_{3})+\lambda _{2}(y_{2}-y_{3})+y_{3}-y=0}$

Biến đổi tuyến tính có thể viết gọn là

${\displaystyle {\overrightarrow {T}}\cdot {\overrightarrow {\lambda }}={\vec {r}}-{\vec {r}}_{3}}$

với ${\displaystyle {\vec {\lambda }}}$ là vector có tọa độ barycentric, r là vector có tọa độ Cartesian và ${\displaystyle {\overrightarrow {T}}}$ là ma trận được cho bởi

${\displaystyle \left({\begin{matrix}x_{1}-x_{3}&x_{2}-x_{3}\\y_{1}-y_{3}&y_{2}-y_{3}\\\end{matrix}}\right)}$

${\displaystyle {\overrightarrow {T}}}$ khả nghịch khi ${\displaystyle {\vec {r}}_{1}-{\vec {r}}_{3}}$ và ${\displaystyle {\vec {r}}_{2}-{\vec {r}}_{3}}$ độc lập tuyến tính (nếu đây không phải là trường hợp, ${\displaystyle {\vec {r}}_{1},{\vec {r}}_{2},{\vec {r}}_{3}}$ có thể là song tuyến tính và không cấu thành tam giác). Thật vậy, ta có thể thế số trên vào phương trình để

${\displaystyle \left({\begin{matrix}\lambda _{1}\\\lambda _{2}\end{matrix}}\right)={\overrightarrow {T}}^{-1}({\overrightarrow {r}}-{\overrightarrow {r}}_{3})\,}$

Quá trình đi tìm tọa barycentric không khác gì đi tìm ma trận khả nghịch của ${\displaystyle {\overrightarrow {T}},}$ khá dễ dàng trong trường hợp ma trận 2×2. Rõ ràng ta thấy các công thức tính tọa độ barycentric của điểm r về tọa độ Cartesian của chúng (x,y) và về tọa độ Cartesian của hệ điểm trong tam giác sẽ có là

${\displaystyle \lambda _{1}={\frac {(y_{2}-y_{3})(x-x_{3})+(x_{3}-x_{2})(y-y_{3})}{\det(T)}}={\frac {(y_{2}-y_{3})(x-x_{3})+(x_{3}-x_{2})(y-y_{3})}{(y_{2}-y_{3})(x_{1}-x_{3})+(x_{3}-x_{2})(y_{1}-y_{3})}}\,,}$

với ${\displaystyle \mathbf {R} =\left({\begin{matrix}\mathbf {r} _{1}|\mathbf {r} _{2}|\mathbf {r} _{3}\end{matrix}}\right)}$

${\displaystyle \lambda _{2}={\frac {(y_{3}-y_{1})(x-x_{3})+(x_{1}-x_{3})(y-y_{3})}{\det(T)}}={\frac {(y_{3}-y_{1})(x-x_{3})+(x_{1}-x_{3})(y-y_{3})}{(y_{2}-y_{3})(x_{1}-x_{3})+(x_{3}-x_{2})(y_{1}-y_{3})}}\,,}$

${\displaystyle \lambda _{3}=1-\lambda _{1}-\lambda _{2}\,.}$

Một cách khác để chuyển đổi từ tọa độ Cartesian sang tọa độ barycentric để viết lại biểu thức dưới dạng ma trận

${\displaystyle {\vec {r}}={\vec {R}}{\vec {\lambda }}}$

với ${\displaystyle {\overrightarrow {R}}=\left({\begin{matrix}{\vec {r}}_{1}|{\vec {r}}_{2}|{\vec {r}}_{3}\end{matrix}}\right)}$ và

${\displaystyle {\vec {\lambda }}=\left(\lambda _{1},\lambda _{2},\lambda _{3}\right)^{\top }.}$

Và điều kiện ${\displaystyle \lambda _{1}+\lambda _{2}+\lambda _{3}=1}$ ghi chú ${\displaystyle \left(1,1,1\right){\vec {\lambda }}=1}$ và tọa độ barycentric có thể được giải quyết như các giải pháp của các hệ tuyến tính

${\displaystyle \left({\begin{matrix}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\1&1&1\end{matrix}}\right){\vec {\lambda }}=\left({\begin{matrix}x\\y\\1\end{matrix}}\right)}$

Chuyển đổi giữa tọa độ barycentric và tọa độ tam tuyến tính

Một điểm có tọa độ tam tuyến tính x:y:z có tọa độ barycentric ax:by:cz với a, b và c là các độ dài phụ của tam giác nào đó. Nhưng ngược lại, một điểm có tọa độ barycentric α:β:γ sẽ có tọa độ tam tuyến tính α/a:β/b:γ/c.

Ứng dụng: Xác định vị trí đối với một tam giác

Ứng dụng: Phép nội suy trên lưới phi cấu trúc tam giác

Ứng dụng: Tích phân trên một tam giác

Ví dụ

Đường tròn ngoại tiếp của một tam giác ABC có tọa độ barycentric

${\displaystyle a^{2}(-a^{2}+b^{2}+c^{2}):\;b^{2}(a^{2}-b^{2}+c^{2}):\;c^{2}(a^{2}+b^{2}-c^{2})\,}$

${\displaystyle =\sin 2A:\sin 2B:\sin 2C,}$

với a, b và c lần lượt là độ dài các cạnh BC, CA, AB của một tam giác. Trực tâm của tam giác cũng tương tự

${\displaystyle \tan A:\tan B:\tan C.}$

Incenter cũng có

${\displaystyle a:b:c=\sin A:\sin B:\sin C.}$

Tâm cửu-điểm cũng có

${\displaystyle a\cos(B-C):b\cos(C-A):c\cos(A-B)}$

${\displaystyle =a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}:b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}:c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}.}$

Tọa độ trên một tứ diện

Ở đây biểu thức lại được biểu diễn dưới dạng biến đổi tuyến tính (nhưng khác ở chỗ là chúng ta đang xét trên một tứ diện trong ${\displaystyle \mathbb {R} ^{3}}$ nên nó có 4 điểm - thì sẽ có 4 thành phần số trong tọa độ

${\displaystyle \left({\begin{matrix}\lambda _{1}\\\lambda _{2}\\\lambda _{3}\end{matrix}}\right)={\overrightarrow {T}}^{-1}({\overrightarrow {r}}-{\overrightarrow {r}}_{4})\,}$

trong đó ${\displaystyle {\overrightarrow {T}}}$ là một ma trận cấp 3×3:

${\displaystyle {\overrightarrow {T}}=\left({\begin{matrix}x_{1}-x_{4}&x_{2}-x_{4}&x_{3}-x_{4}\\y_{1}-y_{4}&y_{2}-y_{4}&y_{3}-y_{4}\\z_{1}-z_{4}&z_{2}-z_{4}&z_{3}-z_{4}\end{matrix}}\right).}$

Tham khảo

Sách tham khảo

• Bradley, Christopher J. (2007). The Algebra of Geometry: Cartesian, Areal and Projective Co-ordinates. Bath: Highperception. ISBN 978-1-906338-00-8.
• Coxeter, H.S.M. (1969). Introduction to geometry (ấn bản thứ 2). John Wiley and Sons. tr. 216–221. ISBN 978-0-471-50458-0. Zbl 0181.48101.
• Barycentric Calculus In Euclidean And Hyperbolic Geometry: A Comparative Introduction Lưu trữ 2012-05-19 tại Wayback Machine, Abraham Ungar, World Scientific, 2010
• Hyperbolic Barycentric Coordinates, Abraham A. Ungar, The Australian Journal of Mathematical Analysis and Applications, Vol.6, No.1, Article 18, pp. 1–35, 2009
• Weisstein, Eric W., "Areal Coordinates" từ MathWorld.
• Weisstein, Eric W., "Barycentric Coordinates" từ MathWorld.