Tốc độ âm thanh

Đo đạc âm thanh
Đặc tính	Ký hiệu
Áp suất âm thanh	p, SPL
Vận tốc hạt	v, SVL
Dịch chuyển hạt	δ
Cường độ âm thanh	I, SIL
Công suất âm thanh	P, SWL
Năng lượng âm thanh	W
Mật độ năng lượng âm thanh	w
Phơi nhiễm âm thanh	E, SEL
Trở kháng âm thanh	Z
Vận tốc âm thanh	c
Tần số âm thanh	AF
Tổn thất truyền đạt	TL
	x; t; s;

Vận tốc âm thanh hay tốc độ âm thanh là tốc độ của sự lan truyền sóng âm thanh trong một môi trường truyền âm (xét trong hệ quy chiếu mà môi trường truyền âm đứng yên). Vận tốc này thay đổi tuỳ thuộc vào môi trường truyền âm (ví dụ âm thanh truyền trong nước nhanh hơn trong không khí) và các điều kiện vật lý/hóa học của môi trường này, như nhiệt độ. Trong những môi trường truyền âm dị hướng, vận tốc âm thanh có độ lớn phụ thuộc vào hướng lan truyền. Trong những môi trường đẳng hướng, độ lớn của vận tốc âm thanh không thay đổi theo hướng lan truyền.

Trong nhiều lĩnh vực của đời sống, thuật ngữ này thường được dùng để chỉ tốc độ của âm thanh trong không khí (khí quyển Trái Đất); một môi trường truyền âm thông dụng, đẳng hướng. Ở mực nước biển, tại nhiệt độ 21 °C (70 °F) và với áp suất tiêu chuẩn, tốc độ âm thanh trong không khí là khoảng khoảng 343.2 m/s (768 mph hay 1236 km/h). Nhưng âm thanh không thể truyền trong chân không, vì do trong chân không không có các hạt cấu tạo để truyền trong âm thanh, còn sở dĩ âm thanh truyền trong các chất lỏng khí rắn vì do các hạt cấu tạo trong chúng chuyển động làm dao động âm thanh. Âm thanh có ý nghĩa lớn với con người và có nhiều ứng dụng trong cuộc sống. Do tác động của con người làm ô nhiễm tiếng ồn, gây nhiều ảnh hưởng xấu đến sức khỏe của con người, cho nên con người đã tìm cách chống ô nhiễm tiếng ồn cụ thể như: trồng cây ngay chỗ dân cư vì khi âm thanh đến gặp tán cây sẽ bị phân tán ra theo mỗi hướng, hoặc dùng tấm vải nhung để chống tiếng ồn.

Lịch sử

Isaac Newton đã tính vận tốc âm thanh là 979 foot trên giây (298 m/s), bị thấp khoảng 15%,^[1] ông đã bỏ qua hiệu ứng biến động nhiệt; cái mà sau này đã được sửa chữa bởi Laplace.^[2]

Trong thế kỷ XVII, đã có những cố gắng trong việc đo tốc độ âm thanh một cách chính xác, bao gồm tính toán Marin Mersenne năm 1630 (1.380 Parisian feet trên giây), Pierre Gassendi năm 1635 (1.473 Parisian feet trên giây) và Robert Boyle (1.125 Parisian trên giây).^[3]

Năm 1709, William Derham, đã xuất bản một tính toán chính xác hơn, 1.072 Parisian feet trên giây.^[3] Derham sử dụng kính viễn vọng từ tháp nhà thờ St Laurence, Upminster để quan sát tia sát từ súng ngắn được bắn ở xa, và sau đó đo thời gian ông ấy nghe thấy tiếng súng với quả lắc nửa giây. Các đo đạc về phát súng đã được thực hiện từ một số địa danh địa phương, bao gồm nhà thờ Bắc Ockendon. Khoảng cách được tính bởi phép đạc tam giác, và do đó tốc độ âm thanh di chuyển được tính.^[4]

Công thức

Tốc độ âm thanh trong ký hiệu toán học là chữ c, trong tiếng Latin celeritas nghĩa là "vận tốc".

Tốc độ âm thanh c được đưa ra bởi phương trình Newton–Laplace:

c={\sqrt {\frac {K_{s}}{\rho }}},

trong đó

K_s là hệ số của độ cứng, mô đun khối đẳng entropy (hoặc mô đun đàn hồi khối với chất khí);
ρ là khối lượng riêng.

Do đó Tốc độ âm thanh tăng lên cùng với độ cứng (sự kháng lại biến đổi dưới tác dụng lực của vật đàn hồi) của chất liệu, và giảm khi khối lượng riêng tăng lên. Với khí lý tưởng mô đun khối K đơn giản là áp suất khi nhân với chỉ số đoạn nhiệt, cái mà có giá trị khoảng 1,4 với khí trong điều kiện áp suất nhiệt độ thường.

Với phương trình trạng thái tổng quát, nếu cơ học cổ điển được sử dụng, tốc độ âm thanh c là

c={\sqrt {\left({\frac {\partial p}{\partial \rho }}\right)_{s}}},

trong đó

p là áp suất;
ρ là khối lượng riêng và đạo hàm đượng tính theo đẳng entropy, ở hằng số entropy s.

Nếu hiệu ứng tương đối hẹp là quan trọng, tốc độ âm thanh được tính theo phương trình tương đối Euler.

Công thức thực hành cho không khí khô

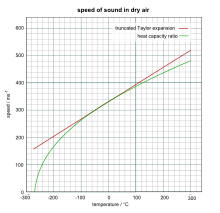
Tốc độ xấp xỉ của âm thanh trong không khí khô (độ ẩm 0%), đơn vị mét trên giây, ở nhiệt độ gần 0 °C, có thể được tính từ

c_{\mathrm {air} }=(331,3+0,606\cdot \vartheta )~~~\mathrm {m/s} ,

trong đó $\vartheta$ là nhiệt độ Celsius (°C).

Phương trình này được suy ra từ hai số hạng đầu tiên trong chuỗi Taylor từ phương trình chính xác hơn ban đầu:

c_{\mathrm {air} }=331,3~{\sqrt {1+{\frac {\vartheta }{273,15}}}}~~~~\mathrm {m/s} .

Chia phần đầu tiên và nhân phần thứ hai ở vế phải cho √273,15 được

c_{\mathrm {air} }=20,05~{\sqrt {\vartheta +273,15}}~~~~\mathrm {m/s} .

Giá trị 331,3 m/s, ở nhiệt độ 0 °C (hoặc 273,15 K), là dựa trên giá trị của tỉ lệ nhiệt dung γ theo lý thuyết (và một vài tính toán), cũng như trên thực tế ở 1 atm không khi thật được mô tả xấp xỉ bằng khí lý tưởng. Giá trị phổ biến của tốc độ âm thanh ở 0 °C có thể thay đổi từ 331,2 đến 331,6 do do các giả định khi nó được tính toán. Nếu cho khí lý tưởng γ là đúng 7/5 = 1,4, tốc độ 0 °C được tính là 331,3 m/s, với các hệ số sử dụng bên trên.

Phương trình này đúng với phạm vi nhiệt độ rộng hơn nhiều, nhưng vẫn dựa trên tỉ lệ nhiệt dung xấp xỉ phụ thuộc vào nhiệt độ, và vì lý do này nó không đúng với nhiệt độ cao hơn. Nó đưa ra dự đoán tốt về các điều kiện tương đối khô, mát, lạnh, áp suất thất, ví dụ như tầng bình lưu của Trái Đất. Phương trình không đúng với áp xuất quá thấp và bước sóng ngắn, do sự phụ thuộc vào giả định là bước sóng của âm thanh trong khí lớn hơn nhiều quãng đường tự do trung bình giữa các va chạm phân tử khí.

Đồ thị so sánh kết quả của hai phương trình ở phía bên phải, sử dụng giá trị hơi khác là 331,5 m/s cho tốc độ âm thanh ở 0 °C.

Số Mach

Số Mach, một đại lượng hữu ích trong khí động lực học, là tỉ lệ giữa tốc độ không khí và tốc độ âm thanh. Ở độ cao, do một số lý do được giải thích, số Mach là một hàm nhiệt độ.

Dụng cụ bay của máy bay, tuy nhiên, sử dụng đạo hàm áp suất để tính số Mach thay vì nhiệt độ. Sự giải định là có một áp suất nhất định ở một độ cao, do đó có nhiệt độ nhất định. Dụng cụ bay của máy bay cần vận hành theo cách này vì áp lực trì trệ được cảm nhận bởi ống Pitot phụ thuộc vào độ cao và tốc độ.

Thông tin

Bảng

Trong bầu không khí tiêu chuẩn:

T₀ là 273,15 K (= 0 °C = 32 °F), đưa ra giá trị trên lý thuyết là 331,3 m/s (= 1086,9 ft/s = 1193 km/h = 741,1 dặm/h = 644,0 kn). Tuy nhiên các giá trị trong khoảng 331,3 - 331,6 có thể tìm thấy trong các tài liệu tham khảo;
T₂₀ là 293,15 K (= 20 °C = 68 °F), đưa ra giá trị 343,2 m/s (= 1126,0 ft/s = 1236 km/h = 767,8 mph = 667,2 kn);
T₂₅ là 298,15 K (= 25 °C = 77 °F), đưa ra giá trị 346,1 m/s (= 1135,6 ft/s = 1246 km/h = 774,3 mph = 672,8 kn).

Trên thực tế, trong khí lý tưởng, tốc độ âm thanh c chỉ phục thuộc vào nhiệt độ, không phải áp suất hay khối lượng riêng. Không khí gần như là khí lý tưởng. Nhiệt độ không khí thay đổi với độ cao, tạo ra thay đổi trong tốc độ âm thanh.

Tác động của nhiệt độ lên các tính chất của không khí
Nhiệt độ T (Celsius\|°C)	Tốc độ âm thanh c (m/s)	Khối lượng riêng của không khí ρ (kg/m³)	Trở kháng âm thanh đặc trưng riêng z₀ (Pa·s/m)
35	351,88	1,1455	403,2
30	349,02	1,1644	406,5
25	346,13	1,1839	409,4
20	343,21	1,2041	413,3
15	340,27	1,2250	416,9
10	337,31	1,2466	420,5
5	334,32	1,2690	424,3
0	331,30	1,2922	428,0
−5	328,25	1,3163	432,1
−10	325,18	1,3413	436,1
−15	322,07	1,3673	440,3
−20	318,94	1,3943	444,6
−25	315,77	1,4224	449,1

Trong điều kiện khí quyển thường, nhiệt độ và do đó cả tốc độ âm thanh thay đổi với độ cao:

Độ cao	Nhiệt độ	m/s	km/h	dặm/h	kn
Mực nước biển	15 °C (59 °F)	340	1.225	761	661
11.000 m−20.000 m (Độ cao của động cơ thương mại, và chuyến bay siêu âm đầu tiên)	−57 °C (−70 °F)	295	1.062	660	573
29.000 m (chuyến bay của X-43A)	−48 °C (−53 °F)	301	1.083	673	585

Môi trường không có khí

Vận tốc âm thanh trong chất rắn

Chất rắn ba chiều

Trong một chất rắn, có một độ cứng khác không đối với cả biến dạng thể tích và biến dạng cắt. Do đó, có thể tạo là sóng âm với các vận tốc khác nhau phụ thuộc vào kiểu biến dạng. Sóng âm tạo ra biến dạng thể tích (sự nén) và biến dạng cắt (sự cắt) được gọi là sóng áp suất (sóng ngang) và sóng cắt (sóng dọc), lần lượt. Trong động đất, các sóng địa chất tương ứng được gọi là sóng P (sóng sơ cấp) và sóng S (sóng thứ cấp), lần lượt. Vận tốc âm thanh của hai loại sóng này truyền trong một vật rắn ba chiều đồng nhất lần lượt là^[6]

c_{chất rắn,p} $={\sqrt {\frac {K+{\frac {4}{3}}G}{\rho }}}={\sqrt {\frac {E(1-\nu )}{\rho (1+\nu )(1-2\nu )}}},$

c_{chất rắn,s} $={\sqrt {\frac {G}{\rho }}},$

với

K là mô đun khối của vật liệu đàn hồi;
G là mô đun cắt của vật liệu đàn hồi;
E là mô đun Young;
ρ là khối lượng riêng;
ν là tỷ lệ Poisson.

Đại lượng cuối cùng không phải một đại lượng độc lập, vì E = 3K(1 − 2ν). Chú ý rằng vận tốc của sóng áp suất phụ thuộc vào cả tính chất kháng áp suất và cắt của vật liệu, trong khi vận tốc sóng cắt chỉ phụ thuộc vào tính chất cắt.

Điển hình, sóng áp suất di chuyển nhanh hơn trong các vật liệu so với sóng cắt, và trong động đất đây là lý sự bắt đầu của một trận động đất thường được theo trước bởi một chấn động nhanh lên xuống, trước khi sóng mà tạo ra chuyển động từ bên này qua bên kia đi tới. Ví dụ, một hợp kim thép điển hình, K = 170 GPa, G = 80 GPa và ρ = 7,700 kg/m³, đưa ra vận tốc nén c_{chất rắn,p} là 6,000 m/s.^[6] Điều này tương đối thỏa mãn với c_{chất rắn,p} đo một cách thực nghiệm ở 5.930 m/s đối với một loại (có thể khác) thép.^[7] Vận tốc cắt c_{chất rắn,s} được ước lượng ở 3.200 m/s bằng cách sử dụng các số liệu tương tự.

Chất rắn một chiều

Vận tốc âm thanh đối với sóng áp suất trong chất liệu cứng như là kim loại đôi khi được tính với một "dây dài" vật liệu cho trước, trong đó vận tốc dễ đo hơn. Trong dây mà có đường kính ngắn hơn một bước sóng, vận tốc sóng áp suất tinh khiết có thể giản ước và tính bởi:

c_{chất rắn} $={\sqrt {\frac {E}{\rho }}},$

với E là mô đun Young. Nó tương tự với công thức của sóng cắt, nhớ rằng mô đun Young thay thế mô đun cắt. Vận tốc âm thanh này với sóng áp suất trong dây dày sẽ luôn ít hơn một chút so với vận tốc tương tự trong chất rắn ba chiều đồng nhất, và tỷ lệ vận tốc trong hai loại vật khác nhau phụ thuộc vào tỷ lệ Poisson của vật liệu.

Vận tốc âm thanh trong chất lỏng

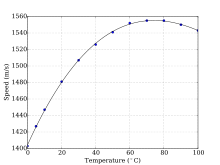
Trong chất lỏng độ cứng khác không duy nhất là biến dạng thể tích (chất lỏng không duy trì lực cắt).

Do đó vận tốc âm thanh trong chất lỏng là

c_{chất lỏng}

={\sqrt {\frac {K}{\rho }}},

với K là mô đun khối của chất lỏng.

Nước

Trong nước trong, âm thanh di chuyển khoảng 1481 m/s tại 20 °C (xem Liên kết ngoài).^[8] Ứng dụng của âm thanh dưới nước có thể được thấy ở sonar, liên lạc âm thanh và hải dương học âm thanh.

Nước biển

Trong nước mối không có bọt khí hoặc trầm tích lơ lửng, âm thanh di chuyển khoảng 1500 m/s (1500.235 m/s tại 1000 kilopascal, 10 °C và độ mặn 3% bởi một phương pháp).^[9] Vận tốc âm thanh trong nước biển phụ thuộc vào áp suất (do đó là độ sâu), nhiệt độ (thay đổi 1 °C ~ 4 m/s), và độ mặn (thay đổi 1‰ ~ 1 m/s), và phương trình thực nghiện được chứng minh để tính toán chính xác vận tốc âm thanh từ các biến này.^[10]^[11] Các hệ số khác tác động đến vận tốc của âm thanh không đáng kể. Vì nhiệt độ giảm với độ sâu trong khi áp suất và độ mặn tăng, đồ thị vận tốc với độ sâu thường cho thấy một đường cong đặc trưng mà giảm tới cực tiểu ở độ sâu vài tăm mét, sau đó tăng lại với độ sâu tăng lên (bên phải).^[12] Để biết thêm thông tin xem Dushaw et al.^[13]

Một phương trình thực nghiệm đơn giản cho vận tốc âm thanh trong nước biển với độ chính xác tương đối cho các đại dương trên thế giới do Mackenzie:^[14]

c(T,S,z)=a_{1}+a_{2}T+a_{3}T^{2}+a_{4}T^{3}+a_{5}(S-35)+a_{6}z+a_{7}z^{2}+a_{8}T(S-35)+a_{9}Tz^{3},

trong đó

T là nhiệt độ tính theo độ C;
S là độ mặn tính theo phần nghìn;
z là độ sâu tính theo mét.

Hằng số a₁, a₂, …, a₉ là

{\begin{aligned}a_{1}&=1448,96,&a_{2}&=4,591,&a_{3}&=-5,304\times 10^{-2},\\a_{4}&=2,374\times 10^{-4},&a_{5}&=1,340,&a_{6}&=1,630\times 10^{-2},\\a_{7}&=1,675\times 10^{-7},&a_{8}&=-1,025\times 10^{-2},&a_{9}&=-7,139\times 10^{-13},\end{aligned}}

với giá trị kiểm tra 1550,744 m/s đối với T = 25 °C, S = 35 phần nghìn, z = 1.000 m. Phương trình này có sai số tiêu chuẩn 0,070 m/s đối với độ mặn giữa 25 và 40 phần nghìn. Xem Technical Guides. Speed of Sound in Sea-Water Lưu trữ 2008-12-01 tại Wayback Machine đối với tính toán trực tuyến.

Các phương trình khác cho vận tốc âm thanh trong nước biển chính xác trong một loạt các điều kiện khác nhau, nhưng phức tạp hợp nhiều, ví dụ phương trình bởi V. A. Del Grosso^[15] và phương trình Chen-Millero-Li.^[13]^[16]

Vận tốc âm thanh trong plasma

Vận tốc âm thanh trong plasma đối với trường hợp phổ biến mà electron nóng hơn ion (nhưng không nóng hơn quá nhiều) được tính bởi công thức (xem ở đây)

c_{s}=(\gamma ZkT_{\mathrm {e} }/m_{\mathrm {i} })^{1/2}=9.79\times 10^{3}(\gamma ZT_{e}/\mu )^{1/2}~\mathrm {m/s} ,

với

m_i là khối lượng ion;
μ là tỷ lệ khối lượng ion trên khối lượng proton μ = m_i/m_p;
T_e là nhiệt độ electron;
Z là trạng thái điện tích;
k là hằng số Boltzmann;
γ là chỉ số đoạn nhiệt.

Ngược lại với khí, áp suất và khối lượng riêng được cung cấp bởi các thành phần riêng biệt, áp suất bởi electron và khối lượng riêng bởi ion. Hai tính chất được kết hợp qua điện trường thay đổi.

Tham khảo

^ “The Speed of Sound”. mathpages.com. Truy cập ngày 3 tháng 5 năm 2015.
^ Bannon, Mike; Kaputa, Frank. “The Newton–Laplace Equation and Speed of Sound”. Thermal Jackets. Truy cập ngày 3 tháng 5 năm 2015.
^ ^a ^b Murdin, Paul (25 tháng 12 năm 2008). Full Meridian of Glory: Perilous Adventures in the Competition to Measure the Earth. Springer Science & Business Media. tr. 35–36. ISBN 9780387755342.
^ Fox, Tony (2003). Essex Journal. Essex Arch & Hist Soc. tr. 12–16.
^ Nemiroff, R.; Bonnell, J. biên tập (19 tháng 8 năm 2007). “A Sonic Boom”. Astronomy Picture of the Day. NASA. Truy cập ngày 24 tháng 10 năm 2010.
^ ^a ^b L. E. Kinsler et al. (2000), Fundamentals of acoustics, 4th Ed., John Wiley and sons Inc., New York, USA.
^ J. Krautkrämer and H. Krautkrämer (1990), Ultrasonic testing of materials, 4th fully revised edition, Springer-Verlag, Berlin, Germany, p. 497
^ “Speed of Sound in Water at Temperatures between 32–212 oF (0–100 oC) — imperial and SI units”. The Engineering Toolbox.
^ Wong, George S. K.; Zhu, Shi-ming (1995). “Speed of sound in seawater as a function of salinity, temperature, and pressure”. The Journal of the Acoustical Society of America. 97 (3): 1732. doi:10.1121/1.413048.
^ APL-UW TR 9407 High-Frequency Ocean Environmental Acoustic Models Handbook Lưu trữ 2003-04-02 tại Library of Congress Web Archives, pp. I1-I2.
^ Robinson, Stephen (22 tháng 9 năm 2005). “Technical Guides - Speed of Sound in Sea-Water”. National Physical Laboratory. Bản gốc lưu trữ ngày 29 tháng 4 năm 2017. Truy cập ngày 7 tháng 12 năm 2016.
^ “How Fast Does Sound Travel?”. Discovery of Sound in the Sea. University of Rhode Island. Bản gốc lưu trữ ngày 20 tháng 5 năm 2017. Truy cập ngày 30 tháng 11 năm 2010.
^ ^a ^b Dushaw, Brian D.; Worcester, P. F.; Cornuelle, B. D.; Howe, B. M. (1993). “On Equations for the Speed of Sound in Seawater”. Journal of the Acoustical Society of America. 93 (1): 255–275. Bibcode:1993ASAJ...93..255D. doi:10.1121/1.405660.
^ Kenneth V., Mackenzie (1981). “Discussion of sea-water sound-speed determinations”. Journal of the Acoustical Society of America. 70 (3): 801–806. Bibcode:1981ASAJ...70..801M. doi:10.1121/1.386919.
^ Del Grosso, V. A. (1974). “New equation for speed of sound in natural waters (with comparisons to other equations)”. Journal of the Acoustical Society of America. 56 (4): 1084–1091. Bibcode:1974ASAJ...56.1084D. doi:10.1121/1.1903388.
^ Meinen, Christopher S.; Watts, D. Randolph (1997). “Further Evidence that the Sound-Speed Algorithm of Del Grosso Is More Accurate Than that of Chen and Millero”. Journal of the Acoustical Society of America. 102 (4): 2058–2062. Bibcode:1997ASAJ..102.2058M. doi:10.1121/1.419655.