Định lý Ceva

Định lý Ceva^[1] là một định lý phổ biến trong hình học cơ bản. Cho một tam giác ABC, các điểm D, E, và F lần lượt nằm trên các đường thẳng BC, CA, và AB. Định lý phát biểu rằng các đường thẳng AD, BE và CF là những đường thẳng đồng quy khi và chỉ khi:

${\displaystyle {\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=1}$

Ngoài ra, định lý Ceva còn được phát biểu một cách tương đương trong lượng giác rằng: AD,BE,CF đồng quy khi và chỉ khi

${\displaystyle {\frac {\sin \angle BAD}{\sin \angle CAD}}\times {\frac {\sin \angle ACF}{\sin \angle BCF}}\times {\frac {\sin \angle CBE}{\sin \angle ABE}}=1}$.

Định lý Ceva

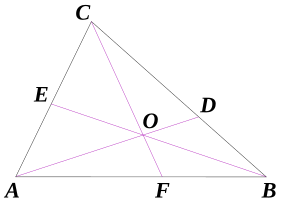
Một đường thẳng đi qua đỉnh của tam giác gọi là đường thẳng Cevian ứng với đỉnh đó.Một trong hình vẽ tam giác ${\displaystyle DEF}$ là một tam giác Cevian của tam giác ABC.

Chứng minh

Giả sử ta có: ${\displaystyle AD}$, ${\displaystyle BE}$ và ${\displaystyle CF}$ đồng quy tại một điểm ${\displaystyle O}$ nào đó (trong hay ngoài tam giác). Do ${\displaystyle \triangle BOD}$ và ${\displaystyle \triangle COD}$ có chung chiều cao (độ dài của đường cao), ta có: ${\displaystyle {\frac {|\triangle BOD|}{|\triangle COD|}}={\frac {BD}{DC}}.}$ Tương tự, ${\displaystyle {\frac {|\triangle BAD|}{|\triangle CAD|}}={\frac {BD}{DC}}.}$

Ta suy ra ${\displaystyle {\frac {BD}{DC}}={\frac {|\triangle BAD|-|\triangle BOD|}{|\triangle CAD|-|\triangle COD|}}={\frac {|\triangle ABO|}{|\triangle CAO|}}(1).}$

Tương tự,${\displaystyle {\frac {CE}{EA}}={\frac {|\triangle BCO|}{|\triangle ABO|}}(2),}$ ${\displaystyle {\frac {AF}{FB}}={\frac {|\triangle CAO|}{|\triangle BCO|}}(3).}$

Nhân ${\displaystyle (1)}$,${\displaystyle (2)}$,${\displaystyle (3)}$ vế theo vế,ta được:${\displaystyle {\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=1}$. Ta có điều phải chứng minh.

Ngược lại, giả sử rằng ta đã có những điểm ${\displaystyle D}$, ${\displaystyle E}$ và ${\displaystyle F}$ thỏa mãn đẳng thức. Gọi giao điểm của ${\displaystyle AD}$ và ${\displaystyle BE}$ là ${\displaystyle O}$, và gọi giao điểm của ${\displaystyle CO}$ và ${\displaystyle AB}$ là ${\displaystyle F'}$. Theo chứng minh trên, ${\displaystyle {\frac {AF'}{F'B}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=1.}$

Kết hợp với đẳng thức trên, ta nhận được: ${\displaystyle {\frac {AF'}{F'B}}={\frac {AF}{FB}}.}$

${\displaystyle \Rightarrow {\frac {AF'+F'B}{F'B}}={\frac {AF+FB}{FB}}\Leftrightarrow {\frac {AB}{F'B}}={\frac {AB}{FB}}.}$

Do đó ${\displaystyle F'B=FB}$, nên ${\displaystyle F}$ và ${\displaystyle F'}$ trùng nhau. Vì vậy ${\displaystyle AD}$, ${\displaystyle BE}$ và ${\displaystyle CF}$ đồng quy tại ${\displaystyle O}$, và định lý đã được chứng minh (là đúng theo cả hai chiều).

Tham khảo thêm

• Định lý Menelaus
• Định lý Carnot
• Định lý Routh
• Định lý Thales

Tham khảo

1. Định lý mang tên nhà toán học người Italia là Giovanni Ceva (1647 - 1734), người tìm ra định lý này vào năm 1698

• Russell, John Wellesley (1905). "Ch. 1 §7 Ceva's Theorem". Pure Geometry. Clarendon Press.
• Grünbaum, Branko; Shephard, G. C. (1995). "Ceva, Menelaus and the Area Principle". Mathematics Magazine. Quyển 68 số 4. tr. 254–268. doi:10.2307/2690569. JSTOR 2690569Bản mẫu:Inconsistent citations.
• Hogendijk, J. B. (1995). "Al-Mutaman ibn Hűd, 11the century king of Saragossa and brilliant mathematician". Historia Mathematica. Quyển 22. tr. 1–18. doi:10.1006/hmat.1995.1001.
• Landy, Steven (tháng 12 năm 1988). "A Generalization of Ceva's Theorem to Higher Dimensions". The American Mathematical Monthly. Quyển 95 số 10. tr. 936–939. doi:10.2307/2322390.
• Masal'tsev, L. A. (1994). "Incidence theorems in spaces of constant curvature". Journal of Mathematical Sciences. Quyển 72 số 4. tr. 3201–3206. doi:10.1007/BF01249519.
• Wernicke, Paul (tháng 11 năm 1927). "The Theorems of Ceva and Menelaus and Their Extension". The American Mathematical Monthly. Quyển 34 số 9. tr. 468–472. doi:10.2307/2300222.