Bài toán Napoléon
Bài toán Napoléon (tiếng Pháp: Problème de Napoléon, tiếng Anh: Napoleon's problem) là một bài toán về dựng hình bằng compa,[1][2] yêu cầu tìm tâm của một đường tròn cho trước. Một phiên bản đơn giản hơn của bài toán là chia đường tròn thành bốn cung bằng nhau chỉ bằng compa.
Napoléon Bonaparte, người được cho là có liên quan đến bài toán này, nổi tiếng với niềm đam mê toán học. Tuy nhiên, không có bằng chứng chắc chắn rằng ông là tác giả hoặc đã giải được bài toán này. Ý tưởng giới hạn việc sử dụng chỉ compa trong các bài toán dựng hình đã được nhà toán học người Ý Lorenzo Mascheroni đề xuất. Tuy nhiên, ý tưởng này cũng xuất hiện trong cuốn sách Euclides Danicus của Georg Mohr, viết từ năm 1672 nhưng chỉ được chú ý rộng rãi từ năm 1928.
Bài viết này trình bày cách giải và chứng minh cho cả hai phiên bản bài toán.
Chia đường tròn thành bốn cung bằng nhau (cho trước tâm)
[sửa | sửa mã nguồn]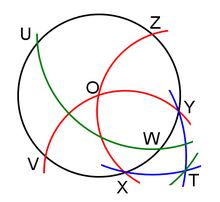
Đề bài
Cho đường tròn tâm O. Chỉ sử dụng compa để chia đường tròn này thành bốn cung bằng nhau.
Cách giải: Ta kí hiệu đường tròn ban đầu là đường tròn C
- Ký hiệu đường tròn ban đầu là C.
- Chọn một điểm X bất kỳ trên C, vẽ đường tròn tâm X, bán kính OX. Đường tròn này cắt C tại V và Y.
- Tương tự, vẽ đường tròn tâm Y, bán kính OX. Đường tròn này cắt C tại X và Z.
- Ta nhận thấy các đoạn thẳng OX, OV, OY, OZ đều bằng bán kính của C.
- Vẽ đường tròn tâm V, bán kính VY và đường tròn tâm Z, bán kính XZ. Hai đường tròn này giao nhau tại T.
- Vẽ đường tròn tâm Z, bán kính OT, cắt C tại U và W. Bốn cung UV, VW, WZ, và ZU chính là bốn cung bằng nhau cần tìm.
Chứng minh
- Các đoạn thẳng OV, OX, OY, OZ bằng bán kính của C.
- Tứ giác OVXY và OZYX là hình thoi, suy ra OX và VY vuông góc.
- Sử dụng định lý Pythagoras trong tam giác vuông VHX, tính được VY=3⋅OX.
- Tương tự, chứng minh OT=2⋅OX.
- Tứ giác UZWV là hình bình hành và cũng là hình thoi, do các cạnh bằng nhau.
- Các cung UV, VW, WZ, ZU bằng nhau vì tứ giác UZWV là hình thoi.
Tìm tâm đường tròn cho trước
[sửa | sửa mã nguồn]Đề bài
Cho một đường tròn bất kỳ. Chỉ sử dụng compa để xác định tâm của nó.[3]
Cách giải

- Gọi (C) là đường tròn cần tìm tâm. Lấy một điểm A bất kỳ trên (C).
- Vẽ một đường tròn (C1) bất kỳ cắt (C) tại B và B′.
- Vẽ hai đường tròn (C2) có tâm lần lượt là B và B′, bán kính AB. Chúng cắt nhau tại C.
- Vẽ đường tròn tâm C, bán kính AC, cắt (C1) tại D và D′.
- Vẽ hai đường tròn tâm lần lượt là D và D′, bán kính AD. Chúng giao nhau tại O, là tâm cần tìm.
Chứng minh:

Ý tưởng của phần chứng minh này là sẽ dựng hình chỉ sử dụng compa để dựng đoạn thẳng độ dài với a; b cho trước và thỏa mãn:
Ta tiếp tục sử dụng hình vẽ của phần dựng hình để chứng minh như sau:
- Vẽ đường tròn (O; OA = a). Để chứng minh O là tâm của (C), ta cần chứng minh nếu (C) có bán kính r thì AO = r.
- Kẻ đường kính AA', lấy dây cung BB' cắt AA' tại H sao cho AB = AB' = b. Vẽ (B; AB = b), đường tròn này cắt OA tại C.
- Ta thấy góc ABA' là góc nội tiếp nửa đường tròn, từ đó suy ra góc này là góc vuông. Ta cũng thấy BH vuông góc với AA', từ đó ta thu được công thức dựa trên hệ thức lượng:
- Từ đó, ta có: , cũng suy ra
- Ta thấy A; B và B' đều nằm trên (C) bán kính r, hơn nữa AB; AB'; BC và B'C đều bằng b, từ đó suy ra , từ đó có được a = r.
- Theo đó, O là tâm của đường tròn (C).
Xem thêm
[sửa | sửa mã nguồn]Tham khảo
[sửa | sửa mã nguồn]- ^ Martinache, Igor (2013). “La fabrique des footballeurs ”. Idées économiques et sociales. N° 171 (1): 78. doi:10.3917/idee.171.0078. ISSN 2257-5111.
- ^ Weisstein, Eric W. “Napoleon's Problem”. mathworld.wolfram.com (bằng tiếng Anh). Truy cập ngày 11 tháng 11 năm 2022.
- ^ Adler, August (1906). Theorie der geometrischen konstruktionen. University of Michigan. Leipzig, G.J. Göschen.
 GIẢM
37%
GIẢM
37%
 GIẢM
40%
GIẢM
40%
 GIẢM
18%
GIẢM
18%
 GIẢM
38%
GIẢM
38%
 GIẢM
19%
GIẢM
19%










