Nhóm Heisenberg

Trong toán học, nhóm Heisenberg ${\displaystyle H}$, được đặt tên theo nhà toán học Werner Heisenberg, là nhóm các ma trận tam giác trên 3 × 3 dưới dạng

${\displaystyle {\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}}$

dưới phép toán phép nhân ma trận. Các phần tử a, b và c có thể được lấy từ bất kỳ vành giao hoán nào có phần tử đơn vị, thường là vành số thực (tạo ra "nhóm Heisenberg liên tục") hoặc vành các số nguyên (tạo ra "nhóm Heisenberg rời rạc").

Nhóm Heisenberg liên tục phát sinh trong việc mô tả các hệ thống cơ lượng tử một chiều, đặc biệt là trong bối cảnh của định lý Stone – von Neumann.

Trường hợp ba chiều

Tích của hai ma trận Heisenberg 3 x 3 được cho bởi:

${\displaystyle {\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}{\begin{pmatrix}1&a'&c'\\0&1&b'\\0&0&1\\\end{pmatrix}}={\begin{pmatrix}1&a+a'&c+ab'+c'\\0&1&b+b'\\0&0&1\\\end{pmatrix}}\,.}$

Dễ thấy rằng bằng việc nhìn vào phần tử ab', nhóm này không phải là nhóm abel.

Phần tử đơn vị của nhóm Heisenberg là ma trận đơn vị còn phần tử nghịch đảo thì được đưa ra bằng

${\displaystyle {\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}^{-1}={\begin{pmatrix}1&-a&ab-c\\0&1&-b\\0&0&1\\\end{pmatrix}}\,.}$

Nhóm Heisenberg là nhóm con của nhóm affine 2 chiều Aff(2): ${\displaystyle {\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}}$ tác động trên ${\displaystyle ({\vec {x}},1)}$ tương ứng với biến đổi affin sau:${\displaystyle {\begin{pmatrix}1&a\\0&1\end{pmatrix}}{\vec {x}}+{\begin{pmatrix}c\\b\end{pmatrix}}}$.

Sau đây là một số ví dụ nổi bật trong trường hợp 3 chiều.

Nhóm Heisenberg liên tục

Nếu a, b, c, là các số thực (trong vành R) thì ta gọi nhóm đó là nhóm Heisenberg liên tục H₃(R).

Nó là nhóm Lie thực lũy linh với chiều bằng 3.

Nhóm Heisenberg rời rạc

Một phần của đồ thị Cayley của nhóm Heisenberg rời rạc, với các phần tử sinh x, y, z như trong văn bản. (Màu chỉ để hỗ trợ thị giác.)

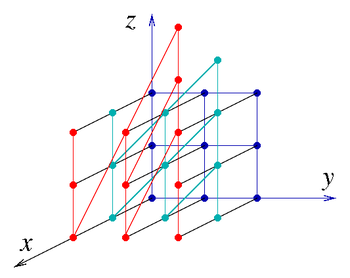
Nếu a, b, c, là các số nguyên (trong vành Z) thì ta gọi nhóm đó là nhóm Heisenberg rời rạc H₃(Z). Nó là nhóm lũy linh không giao hoán. Nó có hai phần tử sinh sau,

${\displaystyle x={\begin{pmatrix}1&1&0\\0&1&0\\0&0&1\\\end{pmatrix}},\ \ y={\begin{pmatrix}1&0&0\\0&1&1\\0&0&1\\\end{pmatrix}}}$

và quan hệ

${\displaystyle z_{}^{}=xyx^{-1}y^{-1},\ xz=zx,\ yz=zy}$,

Với

${\displaystyle z={\begin{pmatrix}1&0&1\\0&1&0\\0&0&1\\\end{pmatrix}}}$

là phần tử sinh tâm của H₃. (Lưu ý rằng các nghịch đảo của x, y và z thay thế 1 ở trên đường chéo chính bằng −1.)

Theo định lý Bass, nó có độ tăng trưởng cấp 4.

Ta có thể viết bất kỳ phần tử nào bằng cách

${\displaystyle {\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}=y^{b}z^{c}x^{a}\,.}$

Nhóm Heisenberg modulo một số nguyên tố lẻ p

Nếu ta lấy a, b, c trong Z/pZ với p là số nguyên tố lẻ, thì ta gọi nhóm đó là nhóm Heisenberg modulo p. Nó là nhóm có cấp p³ với các phần tử sinh x, y và thỏa mãn quan hệ sau:

${\displaystyle z_{}^{}=xyx^{-1}y^{-1},\ x^{p}=y^{p}=z^{p}=1,\ xz=zx,\ yz=zy.}$

Nhóm Heisenberg modulo 2

Nhóm Heisenberg modulo 2 có cấp 8 đẳng cấu với nhóm nhị diện D₄ (các đối xứng của một hình vuông). Quan sát rằng nếu

${\displaystyle x={\begin{pmatrix}1&1&0\\0&1&0\\0&0&1\\\end{pmatrix}},\ \ y={\begin{pmatrix}1&0&0\\0&1&1\\0&0&1\\\end{pmatrix}}}$.

Thì

${\displaystyle xy={\begin{pmatrix}1&1&1\\0&1&1\\0&0&1\\\end{pmatrix}},}$

và

${\displaystyle yx={\begin{pmatrix}1&1&0\\0&1&1\\0&0&1\\\end{pmatrix}}.}$

Các phần tử x và y tương ứng với phản xạ (với 45° giữa chúng), trong khi xy và yx tương ứng với các phép quay 90 °. Các phản xạ khác là xyx và yxy, và quay 180° là xyxy(=yxyx).

Đại số Heisenberg

Đại số Lie ${\displaystyle {\mathfrak {h}}}$ của nhóm Heisenberg ${\displaystyle H}$ (trên các số thực) được gọi là đại số Heisenberg.^[1] Nó được biểu diễn bằng không gian của ma trận vuông kích thước 3×3 dưới dạng^[2]

${\displaystyle {\begin{pmatrix}0&a&c\\0&0&b\\0&0&0\\\end{pmatrix}},}$

với ${\displaystyle a,b,c\in \mathbb {R} }$.

Ba phần tử sau lập thành cơ sở cho ${\displaystyle {\mathfrak {h}}}$,

${\displaystyle X={\begin{pmatrix}0&1&0\\0&0&0\\0&0&0\\\end{pmatrix}};\quad Y={\begin{pmatrix}0&0&0\\0&0&1\\0&0&0\\\end{pmatrix}};\quad Z={\begin{pmatrix}0&0&1\\0&0&0\\0&0&0\\\end{pmatrix}}.}$

Ba phần tử cơ sở này thỏa mãn quan hệ giao hoán,

${\displaystyle [X,Y]=Z;\quad [X,Z]=0;\quad [Y,Z]=0}$.

Tên "nhóm Heisenberg" được lấy cảm hứng từ các quan hệ đó có cùng dạng với các quan hệ giao hoán chính tắc trong cơ học lượng tử.

${\displaystyle \left[{\hat {x}},{\hat {p}}\right]=i\hbar I;\quad \left[{\hat {x}},i\hbar I\right]=0;\quad \left[{\hat {p}},i\hbar I\right]=0,}$

trong đó ${\displaystyle {\hat {x}}}$ là toán tử vị trí, ${\displaystyle {\hat {p}}}$ là toán tử quán tính, và ${\displaystyle \hbar }$ là hằng số Planck.

Nhóm Heisenberg H có tính chất đặc biệt khác là ánh xạ mũ là song ánh từ đại số Lie ${\displaystyle {\mathfrak {h}}}$ sang nhóm H,^[3]

${\displaystyle \exp {\begin{pmatrix}0&a&c\\0&0&b\\0&0&0\\\end{pmatrix}}={\begin{pmatrix}1&a&c+{\frac {ab}{2}}\\0&1&b\\0&0&1\\\end{pmatrix}}.}$

Trong lý thuyết trường bảo giác

Trong lý thuyết trường bảo giác, thuật ngữ đại số Heisenberg được dùng để chỉnh dạng tổng quát vô hạn chiều của đại số. Nó được span bởi các phần tử ${\displaystyle a_{n},n\in \mathbb {Z} }$, cùng các quan hệ giao hoán

${\displaystyle [a_{n},a_{m}]=n\delta _{n+m,0}.}$

Khi bị thay đổi tỷ lệ, thì nó trờ thành số bản sao vô hạn và đếm được của đại số trên.

Số chiều cao hơn

Các nhóm Heisenberg tổng quát ${\displaystyle H_{2n+1}}$ có thể định nghĩa cho số chiều cao hơn trong không gian Euclide, và tổng quát hơn trong không gian vectơ symplectic. Thường hợp tổng quát đơn giản nhất là nhóm Heisenberg thực có số chiều ${\displaystyle 2n+1}$, với bất kỳ ${\displaystyle n\geq 1}$. Bởi là nhóm của các ma trận, ${\displaystyle H_{2n+1}}$ (hoặc ${\displaystyle H_{2n+1}(\mathbb {R} )}$ được dùng để chỉ đây là nhóm các ma trận trên trường ${\displaystyle \mathbb {R} }$ của các số thực ) và được định nghĩa là nhóm các ma trận kích thước ${\displaystyle (n+2)\times (n+2)}$ có các phần tử thuộc ${\displaystyle \mathbb {R} }$ và ma trận nằm dưới dạng sau:

${\displaystyle {\begin{bmatrix}1&\mathbf {a} &c\\\mathbf {0} &I_{n}&\mathbf {b} \\0&\mathbf {0} &1\end{bmatrix}}}$

Trong đó

a là vectơ hàng có độ dài n,

b là vectơ cột có độ dài n,

I_n là ma trận đơn vị bậc n.

Cấu trúc nhóm

Quả thực đây vẫn là một nhóm, bởi phép toán nhân của nó:

${\displaystyle {\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&\mathbf {a} '&c'\\0&I_{n}&\mathbf {b} '\\0&0&1\end{bmatrix}}={\begin{bmatrix}1&\mathbf {a} +\mathbf {a} '&c+c'+\mathbf {a} \cdot \mathbf {b} '\\0&I_{n}&\mathbf {b} +\mathbf {b} '\\0&0&1\end{bmatrix}}}$

và trong nghịch đảo:

${\displaystyle {\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&-\mathbf {a} &-c+\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&-\mathbf {b} \\0&0&1\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&I_{n}&0\\0&0&1\end{bmatrix}}.}$

Đại số Lie

Nhóm Heisenberg là nhóm Lie đơn liên có đại số Lie chứa các ma trận sau

${\displaystyle {\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}},}$

rong đó

a là vectơ hàng có độ dài n,

b là vectơ cột có độ dài n,

0_n là ma trận không bậc n.

Bằng cách đặt e₁, ..., e_n là cơ sở chính tắc của Rⁿ, và đặt

${\displaystyle {\begin{aligned}p_{i}&={\begin{bmatrix}0&\operatorname {e} _{i}^{\mathrm {T} }&0\\0&0_{n}&0\\0&0&0\end{bmatrix}},\\q_{j}&={\begin{bmatrix}0&0&0\\0&0_{n}&\operatorname {e} _{j}\\0&0&0\end{bmatrix}},\\z&={\begin{bmatrix}0&0&1\\0&0_{n}&0\\0&0&0\end{bmatrix}},\end{aligned}}}$

Đại số Lie đi cùng có thể được đặc trưng hóa bằng các quan hệ giao hoán chính tắc,

${\displaystyle {\begin{bmatrix}p_{i},q_{j}\end{bmatrix}}=\delta _{ij}z,\qquad {\begin{bmatrix}p_{i},z\end{bmatrix}}=0,\qquad {\begin{bmatrix}q_{j},z\end{bmatrix}}=0~,}$

(1)

trong đó p₁, ..., p_n, q₁, ..., q_n, z là các phần tử sinh đại số.

Cụ thể hơn, z là phần tử tâm của đại số Lie Heisenberg. Lưu ý rằng đại số Lie của nhóm Heisenberg có tính lũy linh.

Ánh xạ mũ

Đặt

${\displaystyle u={\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}},}$

khi đó ${\displaystyle u^{3}=0_{n+2}}$. Giá trị của ánh xạ mũ qua ${\displaystyle u}$ là

${\displaystyle \exp(u)=\sum _{k=0}^{\infty }{\frac {1}{k!}}u^{k}=I_{n+2}+u+{\tfrac {1}{2}}u^{2}={\begin{bmatrix}1&\mathbf {a} &c+{1 \over 2}\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}.}$

Ánh xạ mũ của bất kỳ đại số Lie lũy linh là vi đồng phôi giữa đại số Lie và nhóm Lie đơn liên liên đới duy nhất đơn liên.

Các ý trên (bên cạnh các mệnh đề về số chiều và nhóm Lie) vẫn áp dụng được khi ta thay R bằng bất kỳ vành giao hoán A. Nhóm tương ứng được ký hiệu là H_n(A ).

Dưới giả định thêm số nguyên tố 2 khả nghịch trong vành A, ánh xạ mũ cũng định được được bởi nó rút gọn thành tổng hữu hạn và có dạng như trên (ví dụ chẳng hạn. A có thể là vành Z/p Z với p là số nguyên tố lẻ hoặc bất kỳ trường đặc số không).

Lý thuyết biểu diễn

Bài chi tiết: Lý thuyết Stone–von Neumann

Lý thuyết biểu diễn của nhóm Heisenberg lúc đầu vẫn còn đơn giản sau – sau được tổng quát hóa bởi lý thuyết Mackey và được giới thiệu trong vật lý lượng tử.

Cho bất kỳ số thực khác không ${\displaystyle \hbar }$, ta có thể định nghĩa biểu diễn unita bất khả quy ${\displaystyle \Pi _{\hbar }}$ của ${\displaystyle H_{2n+1}}$ tác động trên không gian Hilbert${\displaystyle L^{2}(\mathbb {R} ^{n})}$ bằng công thức:^[4]

${\displaystyle \left[\Pi _{\hbar }{\begin{pmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{pmatrix}}\psi \right](x)=e^{i\hbar c}e^{ib\cdot x}\psi (x+\hbar a)}$

Phép biểu diễn này còn được gọi là biểu diễn Schrödinger. Động cơ thúc đẩy của phép biểu diễn này là tác động của các toán tử vị trí và toán tử quán tính được mũ lên trong cơ học lượng tử. Tham số ${\displaystyle a}$ mô tả các phép tịnh tiến trong không gian vị trí, tham số ${\displaystyle b}$ mô tả các phép tịnh tiến trong không gian quán tính, còn tham số ${\displaystyle c}$ thì cho hệ số pha. Hệ số pha được dùng để thu về nhóm các toán tử, bởi phép tịnh tiếp trong không gian vị trí và không gian quán tính không giao hoán với nhau.

Kết quả quan trọng thu về được là định lý Stone–von Neumann, định lý phát biểu rằng mọi biểu diễn unita bất khả quy (liên tục mạnh) của nhóm Heisenberg có tâm tác động không tầm thường thì tương đương với ${\displaystyle \Pi _{\hbar }}$ cho một số ${\displaystyle \hbar }$.^[5] Hoặc là, chúng đều tương đương với đại số Weyl (hoặc đại số CCR) trên không gian symplectic số chiều 2n.

Chú thích

1. Woit, Peter. Topics in Representation Theory: The Heisenberg Algebra (PDF).
2. Hall 2015 Proposition 3.26
3. Hall 2015 Chapter 2, Exercise 9
4. Hall 2013 Proposition 14.7
5. Hall 2013 Theorem 14.8

Tham khảo

• Binz, Ernst; Pods, Sonja (2008). Geometry of Heisenberg Groups. American Mathematical Society. ISBN 978-0-8218-4495-3.
• Hall, Brian C. (2013), Quantum Theory for Mathematicians, Graduate Texts in Mathematics, 267, Springer, ISBN 978-1461471158
• Hall, Brian C. (2015). Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Graduate Texts in Mathematics. 222 . Springer. ISBN 978-3319134666.
• Howe, Roger (1980). “On the role of the Heisenberg group in harmonic analysis”. Bulletin of the American Mathematical Society. 3 (2): 821–843. doi:10.1090/s0273-0979-1980-14825-9. MR 0578375.
• Kirillov, Alexandre A. (2004). “Ch. 2: "Representations and Orbits of the Heisenberg Group”. Lectures on the Orbit Method. American Mathematical Society. ISBN 0-8218-3530-0.
• Mackey, George (1976). The theory of Unitary Group Representations. Chicago Lectures in Mathematics. University of Chicago Press. ISBN 978-0226500522.

Liên kết ngoài

• Groupprops, The Group Properties Wiki Unitriangular matrix group UT(3,p)