Thế Lennard-Jones

Hình 1. Đồ thị hàm thế Lennard-Jones: Thế năng tương tác liên phân tử V_LJ là hàm theo khoảng cách giữa các cặp hạt. Mức thế cực tiểu tại${\displaystyle r=r_{\rm {min}}=2^{1/6}\sigma .}$

Trong hóa học tính toán, vật lý phân tử và hóa lý, thế Lennard-Jones (còn gọi là thế LJ hoặc thế 12-6; được đặt tên theo John Lennard-Jones) là một cặp thế tương tác giữa các phân tử. Trong số tất cả các thế liên phân tử, thế Lennard-Jones có lẽ là thế năng được nghiên cứu rộng rãi nhất.^[1][2] Đây được coi là một mô hình nguyên mẫu cho các tương tác giữa các phân tử đơn giản nhưng có tính thực tế.

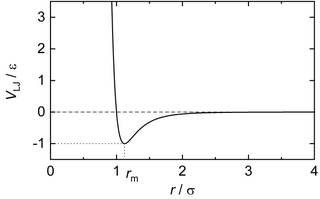
Mô hình thế Lennard-Jones mô tương tác đẩy nhẹ và lực hút yếu (lực hút Van der Waals). Do đó, thế Lennard-Jones mô tả các nguyên tử hoặc phân tử trung hòa điện tử.^[3][4][5] Phương trình thường được sử dụng cho thế Lennard-Jones là$${\displaystyle V_{\text{LJ}}(r)=4\varepsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right],}$$Trong đó r là khoảng cách giữa hai hạt tương tác, ε là độ sâu của hố thế năng (thường được gọi là 'năng lượng phân tán') và σ là khoảng cách (hay độ dài) mà tại đó khi r = σ thì thế năng V của hạt-hạt bằng 0 (thường được gọi là 'kích thước của hạt'). Thế Lennard-Jones đạt giá trị cực tiểu tại khoảng cách ${\displaystyle r=r_{\rm {min}}=2^{1/6}\sigma ,}$ khi đó giá trị ${\displaystyle V=-\varepsilon .}$

Thế Lennard-Jones là một mô hình đơn giản, nhưng mô tả các đặc điểm cơ bản của tương tác giữa các nguyên tử và phân tử đơn giản: Hai hạt tương tác đẩy nhau ở khoảng cách rất gần, hút nhau ở khoảng cách vừa phải và không tương tác ở khoảng cách vô hạn (như đã chỉ ra ở Hình 1)

Cơ học thống kê^[6] và mô phỏng động lực học phân tử (molecular dynamics, MD)^[7][8] nghiên cứu thế Lennard-Jones và thu được các đặc tính nhiệt vật lý của 'chất Lennard-Jones'. Chất Lennard-Jones thường được gọi là 'Lennard-Jonesium',^[2] được coi như là một nguyên tố hóa học (mặc dù đây là hư cấu).^[9] Hơn nữa, các thông số về năng lượng và độ dài có thể được điều chỉnh để phù hợp với nhiều chất "thực" khác nhau. Cả thế năng Lennard-Jones và chất Lennard-Jones đều là những mô hình đơn giản nhưng mang tính thực tế, vì các khái niệm này nắm bắt chính xác các nguyên tắc vật lý thiết yếu như sự hiện diện của điểm tới hạn và điểm ba; sự ngưng tụ và sự đông đặc. Một phần do tính đơn giản về mặt toán học, thế năng Lennard-Jones đã được sử dụng rộng rãi trong các nghiên cứu về vật chất từ thời kỳ bình minh của ngành mô phỏng máy tính.^{[10][11][12][13]} Thế Lennard-Jones có lẽ là mô hình được nghiên cứu nhiều nhất.^[14][9]

Thế Lennard-Jones thường là lựa chọn tiêu chuẩn để phát triển các lý thuyết về vật chất (đặc biệt là vật chất "mềm") cũng như để phát triển và thử nghiệm các phương pháp và thuật toán tính toán. Khi điều chỉnh các tham số mô hình ε và σ thành các đặc tính của chất "thực", thế Lennard-Jones có thể được sử dụng để mô tả các chất đơn giản (ví dụ như khí hiếm) với độ chính xác cao. Hơn nữa, thế Lennard-Jones thường được sử dụng làm "khối xây dựng" trong các mô hình phân tử (còn gọi là trường lực - force field) cho các chất phức tạp hơn.^{[15][16][17][18][19]}

Tham khảo

1. Fischer, Johann; Wendland, Martin (tháng 10 năm 2023). “On the history of key empirical intermolecular potentials”. Fluid Phase Equilibria. 573: 113876. doi:10.1016/j.fluid.2023.113876. ISSN 0378-3812.
2. ^ Lenhard, Johannes; Stephan, Simon; Hasse, Hans (tháng 2 năm 2024). “A child of prediction. On the History, Ontology, and Computation of the Lennard-Jonesium”. Studies in History and Philosophy of Science (bằng tiếng Anh). 103: 105–113. doi:10.1016/j.shpsa.2023.11.007.
3. Jones, J. E. (1924). “On the determination of molecular fields.—I. From the variation of the viscosity of a gas with temperature”. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character (bằng tiếng Anh). 106 (738): 441–462. Bibcode:1924RSPSA.106..441J. doi:10.1098/rspa.1924.0081. ISSN 0950-1207.
4. Jones, J. E. (1924). “On the determination of molecular fields. —II. From the equation of state of a gas”. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character (bằng tiếng Anh). 106 (738): 463–477. Bibcode:1924RSPSA.106..463J. doi:10.1098/rspa.1924.0082. ISSN 0950-1207.
5. Lennard-Jones, J E (1 tháng 9 năm 1931). “Cohesion”. Proceedings of the Physical Society. 43 (5): 461–482. Bibcode:1931PPS....43..461L. doi:10.1088/0959-5309/43/5/301. ISSN 0959-5309.
6. Hill, Terrell L. (1956). Statistical mechanics: principles and selected applications. New York: Dover Publications. ISBN 0-486-65390-0. OCLC 15163657.
7. D. C. Rapaport (1 tháng 4 năm 2004). The Art of Molecular Dynamics Simulation. Cambridge University Press. ISBN 978-0-521-82568-9.
8. Frenkel, D.; Smit, B. (2002), Understanding Molecular Simulation , San Diego: Academic Press, ISBN 0-12-267351-4
9. ^ Stephan, Simon; Thol, Monika; Vrabec, Jadran; Hasse, Hans (28 tháng 10 năm 2019). “Thermophysical Properties of the Lennard-Jones Fluid: Database and Data Assessment”. Journal of Chemical Information and Modeling (bằng tiếng Anh). 59 (10): 4248–4265. doi:10.1021/acs.jcim.9b00620. ISSN 1549-9596. PMID 31609113.
10. Wood, W. W.; Parker, F. R. (1957). “Monte Carlo Equation of State of Molecules Interacting with the Lennard‐Jones Potential. I. A Supercritical Isotherm at about Twice the Critical Temperature”. The Journal of Chemical Physics (bằng tiếng Anh). 27 (3): 720–733. Bibcode:1957JChPh..27..720W. doi:10.1063/1.1743822. ISSN 0021-9606.
11. Rosenbluth, Marshall N.; Rosenbluth, Arianna W. (1954). “Further Results on Monte Carlo Equations of State”. The Journal of Chemical Physics (bằng tiếng Anh). 22 (5): 881–884. Bibcode:1954JChPh..22..881R. doi:10.1063/1.1740207. ISSN 0021-9606.
12. Alder, B. J.; Wainwright, T. E. (1959). “Studies in Molecular Dynamics. I. General Method”. The Journal of Chemical Physics (bằng tiếng Anh). 31 (2): 459–466. Bibcode:1959JChPh..31..459A. doi:10.1063/1.1730376. ISSN 0021-9606.
13. Rahman, A. (19 tháng 10 năm 1964). “Correlations in the Motion of Atoms in Liquid Argon”. Physical Review (bằng tiếng Anh). 136 (2A): A405–A411. Bibcode:1964PhRv..136..405R. doi:10.1103/PhysRev.136.A405. ISSN 0031-899X.
14. Stephan, Simon; Staubach, Jens; Hasse, Hans (2020). “Review and comparison of equations of state for the Lennard-Jones fluid”. Fluid Phase Equilibria (bằng tiếng Anh). 523: 112772. doi:10.1016/j.fluid.2020.112772.
15. Jorgensen, William L.; Maxwell, David S.; Tirado-Rives, Julian (tháng 1 năm 1996). “Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids”. Journal of the American Chemical Society (bằng tiếng Anh). 118 (45): 11225–11236. doi:10.1021/ja9621760. ISSN 0002-7863.
16. Wang, Junmei; Wolf, Romain M.; Caldwell, James W.; Kollman, Peter A.; Case, David A. (15 tháng 7 năm 2004). “Development and testing of a general amber force field”. Journal of Computational Chemistry (bằng tiếng Anh). 25 (9): 1157–1174. doi:10.1002/jcc.20035. ISSN 0192-8651. PMID 15116359.
17. Stephan, Simon; Horsch, Martin T.; Vrabec, Jadran; Hasse, Hans (3 tháng 7 năm 2019). “MolMod – an open access database of force fields for molecular simulations of fluids”. Molecular Simulation (bằng tiếng Anh). 45 (10): 806–814. arXiv:1904.05206. doi:10.1080/08927022.2019.1601191. ISSN 0892-7022.
18. Eggimann, Becky L.; Sunnarborg, Amara J.; Stern, Hudson D.; Bliss, Andrew P.; Siepmann, J. Ilja (2 tháng 1 năm 2014). “An online parameter and property database for the TraPPE force field”. Molecular Simulation (bằng tiếng Anh). 40 (1–3): 101–105. doi:10.1080/08927022.2013.842994. ISSN 0892-7022.
19. Zhen, Shu; Davies, G. J. (16 tháng 8 năm 1983). “Calculation of the Lennard-Jones n–m potential energy parameters for metals”. Physica Status Solidi A. 78 (2): 595–605. Bibcode:1983PSSAR..78..595Z. doi:10.1002/pssa.2210780226.