Điện động lực học lượng tử

Lý thuyết trường lượng tử
Sơ đồ Feynman
Lịch sử
Nền tảng Lý thuyết trường Điện từ học Tương tác yếu Tương tác mạnh Cơ học lượng tử Thuyết tương đối hẹp Thuyết tương đối rộng Lý thuyết trường chuẩn
Đối xứng Đối xứng trong cơ học lượng tử C-symmetry P-symmetry T-symmetry Space translation symmetry Time translation symmetry Rotation symmetry Lorentz symmetry Poincaré symmetry Gauge symmetry Explicit symmetry breaking Spontaneous symmetry breaking Yang–Mills theory Noether charge Topological charge
Công cụ Anomaly Crossing Effective field theory Expectation value Ghost fields Faddeev–Popov ghosts Sơ đồ Feynman Lattice gauge theory LSZ reduction formula Partition function Propagator Lượng tử hóa Regularization Renormalization Trạng thái chân không Wick's theorem Wightman axioms Feynman parametrization
Phương trình Phương trình Dirac Phương trình Klein–Gordon Phương trình Proca equations Phương trình Wheeler–DeWitt Phương trình Bargmann–Wigner Phương trình Joos–Weinberg Phương trình Weyl
Mô hình chuẩn Điện động lực học lượng tử Tương tác điện yếu Thuyết sắc động lực học lượng tử Cơ chế Higgs
Lý thuyết chưa hoàn chỉnh Topological quantum field theory Lý thuyết dây Superstring theory Thuyết M Siêu đối xứng Siêu hấp dẫn Technicolor Thuyết vạn vật Hấp dẫn lượng tử
Nhà khoa học Adler Anderson Bethe Bogoliubov Coleman Callan DeWitt Dirac Dyson Fermi Feynman Fierz Fock Fröhlich Gell-Mann Goldstone Gross Heisenberg 't Hooft Jackiw Jordan Landau Lee Lehmann Mandelstam Majorana Nambu Parisi Polyakov Salam Schwinger Skyrme Stueckelberg Symanzik Tomonaga Veltman Weinberg Weisskopf Weyl Wilczek Wilson Witten Yang Yukawa Zimmermann Zinn-Justin
x t s

Trong vật lý hạt, điện động lực học lượng tử (QED) là lý thuyết trường lượng tử tương đối tính của điện động lực học. Về cơ bản, nó miêu tả cách ánh sáng và vật chất tương tác với nhau và là lý thuyết đầu tiên kết hợp được các tính chất của cơ học lượng tử và thuyết tương đối hẹp. QED miêu tả bằng toán học mọi hiện tượng có sự tham gia của các hạt mang điện tương tác với nhau thông qua trao đổi các photon ảo và biểu diễn các tính chất lượng tử của điện từ học cổ điển mang lại một lý thuyết đầy đủ về tương tác vật chất và ánh sáng.

Theo thuật ngữ kĩ thuật, QED là lý thuyết nhiễu loạn của chân không lượng tử điện từ. Richard Feynman, gọi nó là "viên ngọc của vật lý học" do khả năng tiên đoán chính xác các đại lượng như mômen từ dị thường của electron, dịch chuyển Lamb đối với mức năng lượng của hiđrô.^[1]:Ch1

Lịch sử

Bài chi tiết: Lịch sử cơ học lượng tử

Paul Dirac

Lý thuyết lượng tử đầu tiên miêu tả tương tác giữa bức xạ và vật chất do nhà khoa học người Anh Paul Dirac đưa ra, mà (trong thập niên 1920) ông là người đầu tiên tính được hệ số phát xạ tự phát cho một nguyên tử.^[2]

Dirac miêu tả sự lượng tử hóa của trường điện từ giống như các dao động tử điều hòa và giới thiệu khái niệm toán tử sinh và hủy của hạt. Trong những năm sau, với các đóng góp của Wolfgang Pauli, Eugene Wigner, Pascual Jordan, Werner Heisenberg và hình thức điện động lực học lượng tử sáng rõ nêu bởi Enrico Fermi,^[3] các nhà vật lý tin rằng, về nguyên lý, có thể tính toán bất kỳ một quá trình vật lý nào có sự tham gia của các photon và các hạt điện tích. Tuy nhiên, những nghiên cứu chi tiết hơn của Felix Bloch và Arnold Nordsieck,^[4] và Victor Weisskopf,^[5] trong năm 1937 và 1939, cho thấy những tính toán này chỉ tin cậy đối với xấp xỉ bậc nhất của lý thuyết nhiễu loạn, mà Robert Oppenheimer đã chỉ ra trước đó.^[6] Những chuỗi vô hạn xuất hiện khi tính đến số hạng bậc cao hơn, khiến cho các tính toán trở lên vô nghĩa và dấy lên những nghi ngờ về tính nhất quán nội tại của lý thuyết. Trong thời gian này chưa có một giải pháp nào được nêu ra, và dường như nó không thể tương thích hoàn toàn đối với cả thuyết tương đối hẹp và cơ học lượng tử.

Hans Bethe

Những khó khăn trong lý thuyết tăng lên vào cuối thập niên 1940. Với kỹ thuật mới dựa trên sóng vi ba cho phép thực hiện các thí nghiệm đo chính xác hơn mức dịch chuyển năng lượng đối với nguyên tử hiđrô,^[7] mà ngày nay gọi là dịch chuyển Lamb và mômen từ dị thường của electron.^[8] Những thí nghiệm này cho thấy những giá trị kỳ lạ xuất hiện mà lý thuyết lúc đó không thể giải thích được.

Hans Bethe là người đầu tiên nêu ra giải pháp khắc phục những trở ngại này. Năm 1947, trên chuyến xe lửa từ New York đến Schenectady,^[9] sau khi tham gia hội nghị tổ chức tại Đảo Shelter về chủ đề này, Bethe đã hoàn thành tính toán phi tương đối tính đầu tiên về sự dịch chuyển của các vạch quang phổ của nguyên tử hiđrô mà trước đó Lamb và Retherford đo được.^[10] Mặc dù có những hạn chế trong cách tính của ông, kết quả thu được khớp tuyệt vời so với thực nghiệm. Ý tưởng đơn giản nhằm triệt tiêu các giá trị vô hạn để hiệu chỉnh khối lượng và điện tích thu về giá trị hữu hạn như đo bằng các thí nghiệm. Theo cách này, những giá trị vô hạn sinh bởi chuỗi số bị hấp thụ bởi các hằng số và cho kết quả hữu hạn khớp với giá trị đo được từ thí nghiệm. Thủ tục này sau đó gọi là tái chuẩn hóa.

Feynman (giữa) và Oppenheimer (phải) tại Los Alamos.

Dựa trên trực giác của Bethe và những bài báo cơ sở về lĩnh vực này của Sin-Itiro Tomonaga,^[11] Julian Schwinger,^[12][13] Richard Feynman^[14][15][16] và Freeman Dyson,^[17][18] các nhà vật lý cuối cùng đã có thể tìm ra được những công thức hiệp biến cho giá trị hữu hạn tại bậc xấp xỉ bất kỳ trong chuỗi số miêu tả bằng lý thuyết nhiễu loạn của điện động lực học lượng tử. Sin-Itiro Tomonaga, Julian Schwinger và Richard Feynman cùng nhận giải Nobel Vật lý năm 1965 cho những công trình cơ bản trong ngành này.^[19] Những đóng góp của họ, cùng với của Freeman Dyson, về khuôn khổ lý thuyết hiệp biến và bất biến chuẩn (gauge invariant) của điện động lực học lượng tử cho phép những tính toán về các đại lượng quan sát được tại những bậc xấp xỉ bất kỳ trong lý thuyết nhiễu loạn. Kỹ thuật toán học của Feynman, dựa trên các biểu đồ của ông, ban đầu dường như rất khác lạ so với cách tiếp cận theo lý thuyết trường, và toán tử của Schwinger và Tomonaga, nhưng sau đó Freeman Dyson chứng tỏ rằng hai cách tiếp cận này tương đương với nhau.^[17] Tái chuẩn hóa, kỹ thuật đòi hỏi gắn các đại lượng vật lý tại những phép phân kỳ nhất định xuất hiện trong lý thuyết thông qua các tích phân, sau đó trở thành một trong những công cụ cơ bản của lý thuyết trường lượng tử và trở thành một tiêu chuẩn cho một lý thuyết lượng tử được chấp thuận hay không. Ngay cả khi kỹ thuật tái chuẩn hóa hoạt động khá hiệu quả trong thực hành, Feynman không bao giờ cảm thấy dễ chịu hoàn toàn về tính đúng đắn toán học của nó, và ông coi tái chuẩn hóa giống như "trò xóc đĩa" (shell game) và "hocus pocus" (ma thuật).^[1]:128

QED đã trở thành hình mẫu và khuôn khổ cho những lý thuyết trường lượng tử về sau. Một trong những lý thuyết đó là Sắc động lực học lượng tử QCD, hình thành từ đầu thập niên 1960 và có mô hình như ngày nay kể từ những công trình năm 1975 thực hiện bởi H. David Politzer, Sidney Coleman, David Gross và Frank Wilczek. Dựa trên các công trình tiên phong của Schwinger, Gerald Guralnik, Dick Hagen, và Tom Kibble,^[20][21] Peter Higgs, Jeffrey Goldstone, và những nhà vật lý khác, Sheldon Glashow, Steven Weinberg và Abdus Salam độc lập với nhau chứng minh được lực hạt nhân yếu và điện động lực học lượng tử có thể thống nhất với nhau thành một lý thuyết chung là lý thuyết lực điện - yếu.

Cách nhìn của Feynman về điện động lực học lượng tử

Giới thiệu

Gần cuối cuộc đời mình, Richard P. Feynman đã thực hiện một số bài giảng về QED với mục đích dành cho công chúng. Những bài giảng này được biên soạn và xuất bản thành sách Feynman (1985), QED: The strange theory of light and matter,^[1] với nội dung trình bày theo phong cách cổ điển mà không dùng các phương trình để giải thích QED như được thể hiện dưới đây.

Những điểm chính trong diễn đạt của Feynman về QED bao gồm ba tác dụng cơ bản.^[1]:85

• Một photon đi từ một nơi trong một thời điểm đến nơi khác trong thời điểm khác.
• Một electron đi từ một nơi trong một thời điểm đến nơi khác trong thời điểm khác.
• Một electron phát ra hoặc hấp thụ một photon ở một nơi và thời điểm nhất định.

Các phần tử của sơ đồ Feynman.

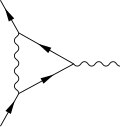
Những tác dụng này được biểu diễn bằng hình ảnh đơn giản cho ba phần tử cơ bản của sơ đồ Feynman: đường dạng sóng thể hiện cho photon, đường thẳng thể hiện cho electron và giao điểm của hai đường thẳng và một đường sóng ở một định biểu diễn electron phát ra hoặc hấp thụ một photon. Xem minh họa các phần tử trong hình bên cạnh.

Một điều quan trọng là không đi sâu vào giải thích chi tiết ở từng sơ đồ này. Nó không hàm ý hay giải thích bằng cách nào một hạt đi từ điểm này đến điểm kia. Sơ đồ cũng không hàm ý rằng các hạt chuyển động theo đường thẳng hay theo đường lượn sóng. Chúng không hàm ý các hạt chuyển động với tốc độ cố định. Để cho thuận tiện, photon thường được biểu diễn bằng đường lượn sóng và không phải bằng đường thẳng cũng không hàm ý rằng nó thể hiện tính chất sóng nhiều hơn so với electron. Các hình ảnh chỉ là những ký hiệu để minh họa các tác dụng ở trên: các photon và electron thực hiện, bằng một cách nào đó, di chuyển từ điểm này đến điểm kia và các electron, bằng một cách nào đó, phát ra và hấp thụ các photon. Lý thuyết không cho chúng ta biết làm cách nào mà những tác dụng này xảy ra, nhưng lý thuyết cho chúng ta biết cách tính xác suất cho nhiều tình huống khác nhau.

Ngoài cách biểu diễn ngắn gọn bằng hình ảnh cho các tác dụng, Feynman cũng giới thiệu một khái niệm ngắn gọn khác cho các đại lượng bằng số gọi là biên độ xác suất. Xác suất bằng bình phương của trị tuyệt đối của tổng biên độ xác suất, ${\displaystyle Prob.=|f(Amplitude)|^{2}}$. Nếu một photon đi từ một nơi này đến nơi khác và tại một thời điểm tương ứng, ví dụ từ A— đến một nơi khác và ở thời điểm tương ứng khác—ví dụ, B—đại lượng miêu tả cho quá trình này được Feynman viết gọn là ${\displaystyle P(AtoB)}$. Đại lượng tương tự cho sự kiện một electron di chuyển từ C đến D được viết bằng E(C to D). Đại lượng cho chúng ta biết biên độ xác suất của sự kiện phát ra hoặc hấp thụ một photon thì ông ký hiệu là 'j'. Đại lượng này có liên hệ với, nhưng không giống nhau, điện tích electron đo được 'e'.^[1]:91

QED dựa trên giả sử rằng các tương tác phức tạp giữa nhiều electron và photon có thể được biểu diễn bằng cách sắp xếp cho phù hợp ba tác dụng cơ bản ở trên, rồi sử dụng các biên độ xác suất để tính xác suất xảy ra bất kỳ một tương tác phức tạp nào. Hóa ra các ý tưởng cơ bản của QED có thể được truyền đạt bằng cách giả sử rằng bình phương của tổng các biên độ xác suất như đã đề cập ở trên (P(A đến B), E(A đến B) và 'j') hoạt động giống như khái niệm xác suất trong toán học. (Một cách đơn giản hóa như thường gặp trong các sách của Feynman.) Sau đó, theo Feynman, giá trị xác suất sẽ được hiệu chỉnh để bao gồm những công thức toán học đặc biệt trong cơ học lượng tử.

Những quy tắc cơ bản của biên độ xác suất mà sẽ được sử dụng là a) nếu một sự kiện có thể xảy ra theo nhiều cách khác nhau thì biên độ xác suất của nó bằng tổng của các biên độ xác suất của các cách khả dĩ và b) nếu một quá trình bao gồm một số các quá trình con độc lập thì biên độ xác suất của nó bằng tích của các biên độ xác suất của các quá trình con.^[1]:93

Những bước cơ bản

Giả sử chúng ta bắt đầu bằng một electron ở một vị trí và thời điểm nhất định (vị trí và thời điểm này được gán bất kỳ bằng ký hiệu A) và một photon ở vị trí và thời điểm khác (ký hiệu là B). Một câu hỏi xuất hiện một cách tự nhiên từ quan điểm vật lý đó là: 'Xác suất để tìm thấy một electron tại C (ở vị trí và thời điểm khác) và một photon tại D (cũng một vị trí và thời điểm khác) bằng bao nhiêu?'. Quá trình đơn giản nhất để có được kết quả cuối cùng này là electron di chuyển từ A đến C (một tác dụng cơ bản) và photon di chuyển từ B đến D (một tác dụng cơ bản khác). Một khi biết được biên độ xác suất của mỗi một quá trình con – E(A đến C) và P(B đến D) – thì chúng ta có thể tính được biên độ xác suất của sự kiện hai quá trình xảy ra cùng nhau bằng cách nhân chúng với nhau, như sử dụng quy tắc b) ở trên. Quá trình này cho ước lượng đơn giản về biên độ xác suất tổng của nó, mà khi lấy bình phương chúng ta thu được xác suất để xảy ra quá trình này.

Tán xạ Compton.

Nhưng cũng có những con đường khác mà kết quả cuối cùng cũng giống như với quán trình ở trên. Electron có thể di chuyển đến một vị trí và thời điểm E mà tại đây nó hấp thụ một photon; sau đó nó tiếp tục di chuyển trước khi phát ra một photon khác tại F; và rồi nó đi tới C ở vị trí bị phát hiện, trong khi photon mới phát ra thì di chuyển tới D. Xác suất của quá trình phức tạp hơn này có thể thu được bằng cách tìm biên độ xác suất của từng tiến trình con: bao gồm ba tác dụng của electron, hai tác dụng của photon và hai đỉnh – một phát ra và một hấp thụ. Chúng ta có thể tìm được tổng biên độ xác suất bằng cách nhân biên độ xác suất của từng tác dụng này, với một vị trí bất kỳ E và F được chọn. Sau đó, chúng ta sử dụng quy tắc a) ở trên, thực hiện cộng tất cả những biên độ xác suất khả dĩ cho mọi vị trí có thể có của E và F. (Phép cộng này trong thực hành không mấy khi gặp, mà thay vào đó được thực hiện bằng tích phân.) Nhưng cũng có một khả năng khác, đó là electron đầu tiên di chuyển đến G nơi nó phát ra một photon mà photon này đi tới D, trong khi electron tiếp tục di chuyển đến H, nơi nó hấp thụ photon đầu tiên, trước khi di chuyển đến C. Một lần nữa, chúng ta có thể tính toán biên độ xác suất của những tiến trình khả dĩ (cho mọi điểm G và H). Chúng ta có thể thu được ước lượng tốt hơn cho tổng biên độ xác suất bằng cách cộng những biên độ xác suất của hai khả năng này (gồm vị trí E và F, G và H) vào ước lượng đơn giản đầu tiên. Một cách trùng hợp, tên gọi cho quá trình một photon tương tác với một electron theo cách này được gọi là tán xạ Compton.

Có vô hạn những quá trình trung gian trong đó thêm nhiều photon bị hấp thụ và/hoặc phát ra. Với mỗi quá trình như vậy có một sơ đồ Feynman tương ứng để miêu tả nó. Điều này hàm ý rằng tính toán trở lên phức tạp cho giá trị biên độ xác suất, nhưng cũng cho thấy đối với trường hợp biểu đồ càng phức tạp thì giá trị đóng góp vào kết quả ban đầu càng ít đi, ở đây chỉ có vấn đề về thời gian và nỗ lực tính toán để tìm ra giá trị càng chính xác hơn so với giá trị ban đầu. Đây là cách tiếp cận tính toán cơ bản của QED. Để tính toán xác suất của bất kỳ quá trình tương tác nào giữa các electron và photon đó là đầu tiên phải chú ý đến, với những sơ đồ Feynman nào mà, mọi cách khả dĩ để quá trình này có thể được xây dựng từ ba phần tử cơ bản miêu tả ở trên. Mỗi sơ đồ bao gồm một số tính toán chứa những quy tắc xác định để tìm ra biên độ xác suất kèm theo.

Cách xây dựng cơ bản trên vẫn còn áp dụng khi chúng ta chuyển sang cách miêu tả theo cơ học lượng tử nhưng cần thay đổi một số khái niệm. Một trong số đó là chúng ta thường nghĩ rằng trong cuộc sống hàng ngày sẽ có một số giới hạn lên những điểm mà hạt có thể di chuyển, nhưng điều này trở lên không còn đúng trong điện động lực học lượng tử. Có khả năng cho một electron tại A, hoặc một photon tại B, di chuyển theo tác dụng cơ bản đến một nơi bất kỳ khác trong một thời điểm bất kỳ trong vũ trụ. Điều này bao gồm cả những vị trí mà chỉ có thể đi tới khi vận tốc đòi hỏi phải lớn hơn tốc độ ánh sáng và thậm chí ở thời điểm sớm hơn. (Một electron đi ngược lại thời gian có thể coi như là một positron di chuyển theo chiều thời gian.)^{[1]:89, 98–99}

Biên độ xác suất

Feynman thay thế các số phức bằng những mũi tên quay định hướng, mà bắt đầu từ lúc photon phát ra và đi đến máy dò hạt. Tổng của mọi mũi tên kết quả biểu diễn tổng xác suất của sự kiện. Trong minh hoạ này, ánh sáng phát ra từ nguồn S phản xạ bởi vài mảnh gương (màu lục) trước khi đi tới máy dò tại P. Tổng (${\displaystyle \Sigma }$) của mọi con đường phải được tính vào. Đồ thị bên dưới miêu tả tổng thời gian di chuyển cho mỗi con đường ở trên.

Cơ học lượng tử giới thiệu một sự thay đổi quan trọng trong cách xác suất được tính toán. Xác suất vẫn được biểu diễn bằng những số thực thông thường mà chúng ta sử dụng trong tính xác suất hàng ngày, nhưng xác suất lượng tử ở đây được tính bằng bình phương biên độ xác suất. Biên độ xác suất là những số phức.

Feynman tránh trình bày với độc giả những số phức toán học bằng cách sử dụng đơn giản nhưng chính xác hình ảnh của chúng như là những mũi tên trên trang sách hay bảng viết. (Không nên nhầm lẫn với các mũi tên của sơ đồ Feynman mà chúng thực sự là những biểu diễn đơn giản của mối liên hệ giữa hai điểm trong không gian ba chiều và một chiều thời gian.) Biên độ của các mũi tên là công cụ miêu tả cơ bản của lý thuyết lượng tử cho thế giới vi mô. Không có lý giải thỏa đáng nào cho câu hỏi tại sao chúng lại cần thiết như vậy. Nhưng thực tế chúng ta phải chấp nhận rằng chúng là một phần cơ bản trong miêu tả của chúng ta về mọi hiện tượng lượng tử. Chúng được liên hệ với ý tưởng xác suất trong toán học bởi quy tắc đơn giản đó là xác suất của một sự kiện bằng bình phương độ lớn của độ dài của mũi tên biên độ tương ứng. Do đó, đối với một quá trình cho trước, nếu có hai biên độ xác suất, v và w, xác suất của quá trình được cho bởi hoặc là

${\displaystyle P=|\mathbf {v} +\mathbf {w} |^{2}}$

hoặc

${\displaystyle P=|\mathbf {v} \,\mathbf {w} |^{2}.}$

Quy tắc giống như phép tính cộng và phép tính nhân, tuy nhiên là giống như miêu tả ở trên. Nhưng thông thường trong đời sống hàng ngày nơi chúng ta thực hiện cộng hoặc nhân các giá trị xác suất, thay vào đó trong điện động lực học lượng tử chúng ta thực hiện cộng hoặc nhân các biên độ xác suất là những số phức.

Phép cộng các biên độ xác suất như đối với số phức.

Phép nhân các biên độ xác suất như quy tắc đối với số phức.

Phép cộng và nhân tương tự trong lý thuyết số phức và được minh họa bằng hình ảnh bên cạnh. Kết quả tổng được tính như sau. Đặt điểm đầu của mũi tên thứ hai vào điểm cuối của mũi tên thứ nhất. Tổng có được chính là mũi tên thứ ba nối trực tiếp từ điểm đầu của mũi tên thứ nhất với điểm cuối của mũi tên thứ hai. Tích của hai mũi tên là một mũi tên mới với độ dài là tích của hai độ dài của hai mũi tên. Hướng của mũi tên kết quả được tìm bằng cách cộng các góc của mỗi mũi tên được xoay theo một hướng quy chiếu: nó cho kết quả góc của phép nhân được xoay tương đối với một hướng quy chiếu.

Sự thay đổi trên, từ các xác suất thành các biên độ xác suất, làm phức tạp thêm các tính toán toán học nhưng không làm thay đổi cách tiếp cận cơ bản đã nêu. Nhưng sự thay đổi này vẫn chưa đủ bởi vì nó chưa tính đến cả photon và electron có đặc điểm là có thể phân cực, hay có nghĩa rằng hướng của chúng trong không gian và thời gian phải được tính đến. Do vậy, P(A đến B) thực sự chứa 16 số phức, hay các mũi tên biên độ xác suất.^{[1]:120–121} Cũng có một số thay đổi nhỏ liên quan tới đại lượng "j", mà phải quay hoặc nhân với 90° cho một số trường hợp phân cực, khi muốn thực hiện các phép tính yêu cầu chính xác cao hơn.

Đi kèm với thực tế rằng electron có thể phân cực còn có thêm những chi tiết nhỏ cần thiết khác liên quan tới tính chất một electron là hạt fermion và tuân theo thống kê Fermi–Dirac. Quy tắc cơ bản là nếu chúng ta có biên độ xác suất cho một quá trình phức tạp với sự tham gia của nhiều hơn một electron, thì khi chúng ta bao gồm vào (mà chúng ta luôn phải tính đến) biểu đồ Feynman bổ sung mà ở đó chúng ta chỉ trao đổi hai electron cho nhau, biên độ kết quả có giá trị ngược dấu – dấu âm – của biên độ đầu tiên. Ví dụ, trường hợp đơn giản nhất đó là hai electron bắt đầu tại A và B và kết thúc tại C và D. Lúc này biên độ xác suất cho toàn bộ sự kiện sẽ được tính toán như là "hiệu", E(A đến D) × E(B đến C) − E(A đến C) × E(B đến D), mà khác với kiến thức chúng ta được học từ lý thuyết xác suất, đó là phép tính "cộng".^{[1]:112–113}

Hàm truyền

Cuối cùng, ta phải tính P (A đến B) và E (C đến D) tương ứng cho biên độ xác suất của photon và electron. Về cơ bản chúng là các nghiệm của phương trình Klein–Gordon mà miêu tả hành xử của biên độ xác suất của photon và phương trình Dirac miêu tả hành xử của biên độ xác suất của electron. P (A đến B) và E (C đến D) được gọi là các hàm truyền Feynman (Feynman propagators). Các khái niệm này được viết chuẩn hóa trong các ấn phẩm chuyên môn như sau:

${\displaystyle P({\mbox{A to B}})\rightarrow D_{F}(x_{B}-x_{A}),\quad E({\mbox{C to D}})\rightarrow S_{F}(x_{D}-x_{C})}$

với ký hiệu ngắn gọn như ${\displaystyle x_{A}}$ là bộ bốn số thực biểu diễn cho tọa độ thời gian và tọa độ không gian ba chiều của sự kiện tại điểm A.

Tái chuẩn hóa khối lượng

Vòng xấp xỉ năng lượng tự tại electron (Electron self-energy loop).

Trong lịch sử xuất hiện một vấn đề mà tồn tại trong khoảng 20 năm của lịch sử điện động lực học lượng tử: mặc dù chúng ta bắt đầu với giả sử gồm ba tác dụng cơ bản "đơn giản", các quy tắc của trò chơi nêu rằng nếu chúng ta muốn tính biên độ xác suất cho một electron từ A đến B chúng ta phải tính mọi con đường khả dĩ: đó là liệt kê ra mọi giản đồ Feynman cho hai điểm đầu cuối này. Do vậy sẽ có một con đường mà electron đi tới C, nó phát ra một photon tại đây và bị hấp thụ tại D trước khi electron đi tới B. Hoặc quá trình này có thể xuất hiện hai lần, thậm chí nhiều hơn. Tựu chung lại chúng ta có một tình huống tựa như ở vấn đề fractal trong đó nếu chúng ta nhìn gần hơn về một đường thì sẽ thấy nó phân nhỏ ra thành tập hợp các đường "đơn giản", mà trong mỗi đường này, nếu tiếp tục nhìn thu nhỏ hơn, thì nó lại được phân thành các đường "đơn giản" khác, và cứ tiếp tục vô hạn như thế. Đây là một tình huống rất khó để giải quyết. Nếu mỗi lần thêm vào chi tiết nó chỉ làm thay đổi nhỏ ở kết quả thì vấn đề không quá tệ, nhưng các nhà vật lý đã gặp thảm họa khi họ tìm thấy sự hiệu chỉnh đơn giản đề cập ở trên dẫn tới biên độ xác suất có giá trị vô hạn. Sau này, vấn đề đã được "khắc phục" bằng kỹ thuật gọi là tái chuẩn hóa. Tuy vậy, chính Feynman vẫn không cảm thấy thoải mái về kỹ thuật này, khi ông gọi nó là "quá trình gàn dở".^[1]:128

Kết luận

Với khuôn khổ nêu ở trên các nhà vật lý đã có thể tính với độ chính xác cao một số tính chất của electron, ví dụ như mômen lưỡng cực từ dị thường. Tuy nhiên, như Feynman chỉ ra, lý thuyết hoàn toàn không giải thích được, ví dụ, tại sao các hạt như electron lại có giá trị khối lượng đo được thực tế như vậy. "Chưa có một lý thuyết thỏa đáng giải thích cho những con số như vậy. Chúng ta sử dụng các con số này trong mọi lý thuyết của chúng ta, nhưng chúng ta chưa hiểu chúng – chúng là gì hay chúng đến từ đâu. Tôi tin rằng từ quan điểm cơ bản, đây là một vấn đề nghiêm trọng và rất thú vị."^[1]:152

Toán học

Về mặt toán học, QED là một lý thuyết chuẩn Abel (abelian gauge theory) với nhóm đối xứng U(1). Trường chuẩn (gauge field), làm trung gian tương tác giữa các trường spin-1/2, là trường điện từ. Lagrangian của QED cho trường spin-1/2 tương tác với trường điện từ được viết theo các đơn vị tự nhiên trong phần thực của^[22]:78

${\displaystyle {\mathcal {L}}={\bar {\psi }}(i\gamma ^{\mu }D_{\mu }-m)\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }}$

với

${\displaystyle \gamma ^{\mu }}$ là các ma trận Dirac;

${\displaystyle \psi }$ là trường bispinor của các hạt spin-1/2 (như trường electron–positron);

${\displaystyle {\bar {\psi }}\equiv \psi ^{\dagger }\gamma ^{0}}$, gọi là "psi-bar", đôi lúc được coi là liên hợp Dirac;

${\displaystyle D_{\mu }\equiv \partial _{\mu }+ieA_{\mu }+ieB_{\mu }\,\!}$ là đạo hàm hiệp biến chuẩn (gauge covariant derivative);

e là hằng số cặp, bằng với điện tích của trường bispinor;

m là khối lượng của electron hoặc positron;

${\displaystyle A_{\mu }}$ là thế-4 hiệp biến của trường điện từ tạo bởi chính electron;

${\displaystyle B_{\mu }}$ là trường ngoài sinh bởi nguồn bên ngoài;

${\displaystyle F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\,\!}$ là tensor điện từ.

Phương trình chuyển động

Thay định nghĩa của D vào Lagrangian thu được

${\displaystyle {\mathcal {L}}=i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -e{\bar {\psi }}\gamma _{\mu }(A^{\mu }+B^{\mu })\psi -m{\bar {\psi }}\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }.\,}$

Từ Lagrangian này, có thể tìm ra phương trình chuyển động cho các trường ψ và A.

Sử dụng phương trình Euler–Lagrange trong lý thuyết trường cho ψ,

${\displaystyle \partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)-{\frac {\partial {\mathcal {L}}}{\partial \psi }}=0\,.}$

(2)

và đạo hàm của Lagrangian theo ψ là

${\displaystyle \partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)=\partial _{\mu }\left(i{\bar {\psi }}\gamma ^{\mu }\right),\,}$

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial \psi }}=-e{\bar {\psi }}\gamma _{\mu }(A^{\mu }+B^{\mu })-m{\bar {\psi }}.\,}$

thay kết quả trên vào phương trình (2) có được

${\displaystyle i\partial _{\mu }{\bar {\psi }}\gamma ^{\mu }+e{\bar {\psi }}\gamma _{\mu }(A^{\mu }+B^{\mu })+m{\bar {\psi }}=0\,}$

với liên hợp Hermit

${\displaystyle i\gamma ^{\mu }\partial _{\mu }\psi -e\gamma _{\mu }(A^{\mu }+B^{\mu })\psi -m\psi =0.\,}$

Chuyển số hạng ở giữa sang vế phải thu được

${\displaystyle i\gamma ^{\mu }\partial _{\mu }\psi -m\psi =e\gamma _{\mu }(A^{\mu }+B^{\mu })\psi \,}$

Vế trái nhìn giống như phương trình Dirac ban đầu, và vế phải là tương tác với trường điện từ.

Sử dụng phương trình Euler–Lagrange cho trường A,

${\displaystyle \partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)-{\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=0\,.}$

(3)

đạo hàm lần này là

${\displaystyle \partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)=\partial _{\nu }\left(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }\right),\,}$

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=-e{\bar {\psi }}\gamma ^{\mu }\psi \,}$

thay trở lại phương trình (3) đi đến

${\displaystyle \partial _{\nu }F^{\nu \mu }=e{\bar {\psi }}\gamma ^{\mu }\psi \,}$

Bây giờ nếu chúng ta áp dụng điều kiện chuẩn Lorenz (Lorenz gauge condition)

${\displaystyle \partial _{\mu }A^{\mu }=0}$

phương trình thu về

${\displaystyle \Box A^{\mu }=e{\bar {\psi }}\gamma ^{\mu }\psi \,,}$

mà chính là phương trình sóng của thế-4, phiên bản QED của phương trình Maxwell cổ điển trong chuẩn Lorenz. (Ký hiệu ô vuông biểu diễn cho toán tử D'Alembert, ${\displaystyle \Box =\partial _{\alpha }\partial ^{\alpha }}$.)

Bức tranh tương tác

Lý thuyết này có thể lượng tử hóa một cách trực tiếp bằng cách coi các phần bosonic và fermionic độc lập với nhau. Điều này cho phép chúng ta xây dựng một tập hợp các trạng thái tiệm cận mà có thể dùng để tính biên độ xác suất cho các quá trình khác nhau. Để có thể thực hiện như vậy, chúng ta phải tính một toán tử tiến hóa, đối với một trạng thái ban đầu ${\displaystyle |i\rangle }$, sẽ cho trạng thái cuối cùng ${\displaystyle \langle f|}$ theo cách có được^[22]:5

${\displaystyle M_{fi}=\langle f|U|i\rangle .}$

Kỹ thuật này cũng được gọi là ma trận S (S-matrix). Toán tử tiến hóa nhận được từ bức tranh tương tác (interaction picture) mà tiến hóa thời gian được cho bởi tương tác Hamiltonian, đó là tích phân trên không gian của số hạng thứ hai của mật độ Lagrangian cho ở trên:^[22]:123

${\displaystyle V=e\int d^{3}x{\bar {\psi }}\gamma ^{\mu }\psi A_{\mu }}$

và cũng vậy, ta có^[22]:86

${\displaystyle U=T\exp \left[-{\frac {i}{\hbar }}\int _{t_{0}}^{t}dt'V(t')\right]}$

với T là toán tử thứ tự thời gian (time ordering operator). Toán tử tiến hóa này chỉ có ý nghĩa như là chuỗi, và cái chúng ta nhận được ở đây đó là chuỗi nhiễu loạn với hằng số cấu trúc tế vi như là tham số phát triển. Chuỗi này được gọi là chuỗi Dyson.

Giản đồ Feynman

Mặc dù sự sáng sủa về mặt ý tưởng trong cách tiếp cận Feynman đối với QED, hầu như không một cuốn sách ban đầu nào về điện động lực học lượng tử có nội dung đi theo cách của ông. Khi thực hiện các tính toán nó sẽ dễ dàng hơn khi làm việc với các biến đổi Fourier của các hàm truyền (propagators). Các thí nghiệm của điện động lực học lượng tử thường chủ yếu là các thí nghiệm tán xạ. Trong lý thuyết tán xạ, các nhà vật lý quan tâm tới động lượng của hạt hơn là vị trí của nó, và sẽ thuận tiện khi nghĩ các hạt đang được sinh ra hoặc bị hủy khi chúng tương tác. Giản đồ Feynman cũng có cái nhìn tương tự như thế, nhưng các đường có những cách giải thích khác hẳn. Đường electron biểu diễn cho một electron với năng lượng và động lượng xác định, và cách giải thích tương tự như thế cho đường photon. Một đỉnh trong giản đồ biểu diễn cho sự hủy của một electron và sinh một hạt khác với sự hấp thụ hoặc phát ra một photon, mỗi hạt có một mức năng lượng và động lượng xác định.

Sử dụng định lý Wick đối với các số hạng của chuỗi Dyson, mọi số hạng của ma trận S (S-matrix, scattering matrix) cho QED có thể tính thông qua kỹ thuật của sơ đồ Feynman. Trong trường hợp này các quy tắc cho sơ đồ được liệt kê dưới đây^{[22]:801–802}

Cùng với các quy tắc này chúng ta phải cộng thêm vào một số hạng nữa cho một vòng xấp xỉ kín hàm ý tích phân trên động lượng ${\displaystyle \int d^{4}p/(2\pi )^{4}}$, vì những hạt nội tại này ("hạt ảo") không bị giới hạn bởi bất kỳ năng lượng–động lượng xác định nào—thậm chí như đòi hỏi ở thuyết tương đối hẹp.

Từ các quy tắc này, chúng ta đi thẳng đến được tính toán biên độ xác suất. Một ví dụ là tán xạ Compton, với một electron và một photon trải qua tán xạ đàn hồi. Giản đồ Feynman được sử dụng trong trường hợp này là^{[22]:158–159}

và do đó chúng ta có thể nhận được biên độ tương ứng ở xấp xỉ bậc nhất của chuỗi nhiễu loạn cho ma trận S:

${\displaystyle M_{fi}=(ie)^{2}{\overline {u}}({\vec {p}}\,',s')\epsilon \!\!\!/\,'({\vec {k}}\,',\lambda ')^{*}{p\!\!\!/+k\!\!\!/+m_{e} \over (p+k)^{2}-m_{e}^{2}}\epsilon \!\!\!/({\vec {k}},\lambda )u({\vec {p}},s)+(ie)^{2}{\overline {u}}({\vec {p}}\,',s')\epsilon \!\!\!/({\vec {k}},\lambda ){p\!\!\!/-k\!\!\!/'+m_{e} \over (p-k')^{2}-m_{e}^{2}}\epsilon \!\!\!/\,'({\vec {k}}\,',\lambda ')^{*}u({\vec {p}},s)}$

mà từ đây tính ra tiết diện tán xạ cho quá trình này.

Tính tái chuẩn hóa

Các số hạng bậc cao hơn có thể được tính trực tiếp từ toán tử tiến hóa (evolution operator) và sơ đồ thể hiện cho những số hạng này chứa những phần tử đơn giản sau^{[22]:ch 10}

• 
  Đóng góp của một vòng xấp xỉ (one-loop) vào hàm phân cực chân không (vancuum polarization) ${\displaystyle \Pi \,}$
• 
  Đóng góp của một vòng xấp xỉ vào hàm năng lượng tự tại electron (electron self-energy function) ${\displaystyle \Sigma \,}$
• 
  Đóng góp của một vòng xấp xỉ vào hàm đỉnh (vertex function) ${\displaystyle \Gamma \,}$

mà, là những vòng kín, hàm ý sự có mặt của các tích phân phân kỳ không mang ý nghĩa toán học. Để vượt qua khó khăn này, các nhà vật lý đã đưa ra kỹ thuật tái chuẩn hóa (renormalization), cho các kết quả có giá trị hữu hạn và rất gần với các phép đo thực nghiệm. Một điều quan trọng cần chú ý rằng tiêu chuẩn cho lý thuyết trở lên có ý nghĩa sau khi tái chuẩn hóa đó là số lượng các giản đồ phân kỳ là hữu hạn. Trong trường hợp này lý thuyết được nói là "tái chuẩn hóa được." Lý do cho điều này là để nhận được giá trị tái chuẩn hóa quan sát được (ví dụ điện tích electron tái chuẩn hóa) chúng ta cần một số hữu hạn các hằng số để duy trì tính ổn định của các giá trị tiên đoán từ lý thuyết. Trong trường hợp của Điện động lực học lượng tử số lượng các giản đồ phân kỳ là chỉ có 3 sơ đồ phân kỳ. Thủ tục này cho các giá trị tiên đoán nằm rất gần với giá trị đo thực nghiệm, chẳng hạn tỷ số từ hồi chuyển electron (electron gyromagnetic ratio).

Tính tái chuẩn hóa đã trở thành một tiêu chuẩn cơ bản để đánh giá tính đúng đắn của một lý thuyết trường lượng tử. Mọi lý thuyết miêu tả các tương tác cơ bản, ngoại trừ tương tác hấp dẫn mà là những lý thuyết lượng tử được nghiên cứu sôi động hiện nay, đều là các lý thuyết tái chuẩn hóa được (renormalizable theories).

Các chuỗi phân kỳ

Freeman Dyson đã chứng minh rằng bán kính hội tụ của các chuỗi nhiễu loạn trong QED bằng 0.^[23] Nội dung cơ bản của lập luận là như sau: nếu hằng số cặp có giá trị âm, điều này sẽ tương đương với hằng số Coulomb có giá trị âm. Hệ quả là tương tác điện từ sẽ bị "đổi ngược lại" khi các điện tích cùng dấu sẽ hút nhau và các điện tích trái dấu sẽ đẩy nhau. Điều này dẫn tới chân không mất ổn định khi nó phân rã thành một đám các electron tập trung về một phía trong vũ trụ và một đám positron tập trung về phía khác trong vũ trụ. Bởi vì lý thuyết là 'yếu' đối với bất kỳ giá trị âm của hằng số cặp, các chuỗi không hội tụ, nhưng là chuỗi tiệm cận (asymptotic series).

Từ quan điểm hiện đại, chúng ta nói rằng QED là lý thuyết trường lượng tử không xác định tốt cho những mức năng lượng cao bất kỳ.^[24] Hằng số cặp tiến tới giá trị vô hạn ở mức năng lượng hữu hạn, dấu hiệu của một cực Landau (Landau pole). Về cơ bản vấn đề này nằm ở chỗ QED dường như chịu ảnh hưởng bởi các vấn đề tính chất lượng tử tầm thường (quantum triviality, khi giá trị quan sát của điện tích "tái chuẩn hóa" của một hạt chỉ tính được bằng 0). Đây là một trong những động cơ thúc đẩy việc nhúng QED vào một lý thuyết thống nhất lớn.

Tham khảo

1. ^ Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 978-0-691-12575-6.
2. P.A.M. Dirac (1927). “The Quantum Theory of the Emission and Absorption of Radiation”. Proceedings of the Royal Society of London A. 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.
3. E. Fermi (1932). “Quantum Theory of Radiation”. Reviews of Modern Physics. 4: 87–132. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.
4. F. Bloch; A. Nordsieck (1937). “Note on the Radiation Field of the Electron”. Physical Review. 52 (2): 54–59. Bibcode:1937PhRv...52...54B. doi:10.1103/PhysRev.52.54.
5. V. F. Weisskopf (1939). “On the Self-Energy and the Electromagnetic Field of the Electron”. Physical Review. 56: 72–85. Bibcode:1939PhRv...56...72W. doi:10.1103/PhysRev.56.72.
6. R. Oppenheimer (1930). “Note on the Theory of the Interaction of Field and Matter”. Physical Review. 35 (5): 461–477. Bibcode:1930PhRv...35..461O. doi:10.1103/PhysRev.35.461.
7. W. E. Lamb; R. C. Retherford (1947). “Fine Structure of the Hydrogen Atom by a Microwave Method,”. Physical Review. 72 (3): 241–243. Bibcode:1947PhRv...72..241L. doi:10.1103/PhysRev.72.241.
8. P. Kusch; H. M. Foley (1948). “On the Intrinsic Moment of the Electron”. Physical Review. 73 (3): 412. Bibcode:1948PhRv...73..412F. doi:10.1103/PhysRev.73.412.
9. Schweber, Silvan (1994). “Chapter 5”. QED and the Men Who Did it: Dyson, Feynman, Schwinger, and Tomonaga. Princeton University Press. tr. 230. ISBN 978-0-691-03327-3.
10. H. Bethe (1947). “The Electromagnetic Shift of Energy Levels”. Physical Review. 72 (4): 339–341. Bibcode:1947PhRv...72..339B. doi:10.1103/PhysRev.72.339.
11. S. Tomonaga (1946). “On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields”. Progress of Theoretical Physics. 1 (2): 27–42. doi:10.1143/PTP.1.27.
12. J. Schwinger (1948). “On Quantum-Electrodynamics and the Magnetic Moment of the Electron”. Physical Review. 73 (4): 416–417. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416.
13. J. Schwinger (1948). “Quantum Electrodynamics. I. A Covariant Formulation”. Physical Review. 74 (10): 1439–1461. Bibcode:1948PhRv...74.1439S. doi:10.1103/PhysRev.74.1439.
14. R. P. Feynman (1949). “Space–Time Approach to Quantum Electrodynamics”. Physical Review. 76 (6): 769–789. Bibcode:1949PhRv...76..769F. doi:10.1103/PhysRev.76.769.
15. R. P. Feynman (1949). “The Theory of Positrons”. Physical Review. 76 (6): 749–759. Bibcode:1949PhRv...76..749F. doi:10.1103/PhysRev.76.749.
16. R. P. Feynman (1950). “Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction”. Physical Review. 80 (3): 440–457. Bibcode:1950PhRv...80..440F. doi:10.1103/PhysRev.80.440.
17. ^ F. Dyson (1949). “The Radiation Theories of Tomonaga, Schwinger, and Feynman”. Physical Review. 75 (3): 486–502. Bibcode:1949PhRv...75..486D. doi:10.1103/PhysRev.75.486.
18. F. Dyson (1949). “The S Matrix in Quantum Electrodynamics”. Physical Review. 75 (11): 1736–1755. Bibcode:1949PhRv...75.1736D. doi:10.1103/PhysRev.75.1736.
19. “The Nobel Prize in Physics 1965”. Nobel Foundation. Truy cập ngày 9 tháng 10 năm 2008.
20. G.S. Guralnik, C.R. Hagen, T.W.B. Kibble (1964). “Global Conservation Laws and Massless Particles”. Physical Review Letters. 13 (20): 585–587. Bibcode:1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585.
21. G.S. Guralnik (2009). “The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles”. International Journal of Modern Physics A. 24 (14): 2601–2627. arXiv:0907.3466. Bibcode:2009IJMPA..24.2601G. doi:10.1142/S0217751X09045431.
22. ^ Peskin, Michael; Schroeder, Daniel (1995). An introduction to quantum field theory . Westview Press. ISBN 978-0201503975.
23. Kinoshita, Toichiro (ngày 5 tháng 6 năm 1997). “Quantum Electrodynamics has Zero Radius of Convergence Summarized from Toichiro Kinoshita”. Truy cập ngày 6 tháng 5 năm 2017.
24. Espriu and Tarrach (30 tháng 4 năm 1996). “Ambiguities in QED: Renormalons versus Triviality”. Physics Letters B. 383: 482–486. arXiv:hep-ph/9604431. Bibcode:1996PhLB..383..482E. doi:10.1016/0370-2693(96)00779-4.

Đọc thêm

Sách phổ thông

• Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 978-0-691-12575-6.

Sách đại học

• De Broglie, Louis (1925). Recherches sur la theorie des quanta [Research on quantum theory]. France: Wiley-Interscience.
• Feynman, Richard Phillips (1998). Quantum Electrodynamics. Westview Press; New Ed edition. ISBN 978-0-201-36075-2.
• Jauch, J.M. (1980). The Theory of Photons and Electrons. Rohrlich, F. Springer-Verlag. ISBN 978-0-387-07295-1.
• Greiner, Walter (2000). Gauge Theory of Weak Interactions. Bromley, D.A.,Müller, Berndt. Springer. ISBN 978-3-540-67672-0.
• Kane, Gordon, L. (1993). Modern Elementary Particle Physics. Westview Press. ISBN 978-0-201-62460-1.
• Miller, Arthur I. (1995). Early Quantum Electrodynamics: A Sourcebook. Cambridge University Press. ISBN 978-0-521-56891-3.
• Milonni, Peter W., (1994) The quantum vacuum - an introduction to quantum electrodynamics. Academic Press. ISBN 0-12-498080-5
• Schweber, Silvian, S. (1994). QED and the Men Who Made It. Princeton University Press. ISBN 978-0-691-03327-3.
• Schwinger, Julian (1958). Selected Papers on Quantum Electrodynamics. Dover Publications. ISBN 978-0-486-60444-2.
• Tannoudji-Cohen, Claude (1997). Photons and Atoms: Introduction to Quantum Electrodynamics. Dupont-Roc, Jacques, and Grynberg, Gilbert. Wiley-Interscience. ISBN 978-0-471-18433-1.

Tạp chí

• Dudley, J.M.; Kwan, A.M. (1996). “Richard Feynman's popular lectures on quantum electrodynamics: The 1979 Robb Lectures at Auckland University”. American Journal of Physics. 64 (6): 694–698. Bibcode:1996AmJPh..64..694D. doi:10.1119/1.18234.

Liên kết ngoài

• Điện động lực học lượng tử tại Từ điển bách khoa Việt Nam
• Quantum electrodynamics tại Encyclopædia Britannica (tiếng Anh)
• Feynman's Nobel Prize lecture describing the evolution of QED and his role in it
• Feynman's New Zealand lectures on QED for non-physicists
• qed.wikina.org - Animations demonstrating QED