Hệ tọa độ xích đạo

Hệ tọa độ xích đạo là hệ tọa độ thiên văn được sử dụng nhiều cho các quan sát bầu trời từ Trái Đất. Nó là hệ tọa độ gắn bó chặt chẽ với hệ tọa độ địa lý, vì ở đây người ta sử dụng chung một mặt phẳng quy chiếu và chung các cực.^[1]^[2] Hình chiếu của xích đạo Trái Đất lên thiên cầu được gọi là xích đạo trời. Tương tự, chiếu các cực địa lý lên thiên cầu ta sẽ có thiên cực Bắc và thiên cực Nam.

Có hai biến thể:

1. Hệ góc giờ cố định so với Trái Đất giống như hệ tọa độ địa lý. Hai tọa độ trong hệ này là:

xích vĩ (δ)
góc giờ (H)

2. Hệ xích kinh cố định so với các sao ở xa (thực ra không hẳn như vậy nếu tính đến các hiện tượng tiến động và chương động). Hai tọa độ trong hệ này là:

xích vĩ (δ)
xích kinh (α)

**Hệ tọa độ xích đạo** sử dụng tọa độ cầu. Mặt phẳng tham chiếu được tạo bởi hình chiếu của xích đạo Trái Đất lên thiên cầu, gọi là xích đạo thiên cầu. Hướng cơ bản được thiết lập bằng cách chiếu quỹ đạo Trái Đất lên thiên cầu, gọi là hoàng đạo, và thiết lập điểm nút lên của hoàng đạo lên xích đạo thiên cầu, gọi là điểm xuân phân. Xích kinh được đo theo chiều đông trên xích đạo thiên cầu, và xích vĩ được đo với chiều dương về phía bắc xích đạo thiên cầu. (Hai cặp tọa độ được thể hiện trên hình.) Hình chiếu của các cực địa lý bắc và nam Trái Đất tạo thành các thiên cực bắc và nam tương ứng.^[3]

Trong một đêm hoặc vài đêm, khi quan sát từ mặt đất, hệ xích kinh có vẻ xoay trên trời cùng với các sao. Điều này là do hệ xích kinh gần như cố định với nền sao, còn Trái Đất quay dưới bầu trời cố định.

Do hiện tượng tiến động và chương động, phương xuân phân (điểm xuân phân, vernal equinox) dùng để làm mốc tính xích kinh và xích vĩ thay đổi chậm trên nền sao. Khi xác định phương xuân phân và tính tọa độ các thiên thể theo mốc này cần dùng phương xuân phân của một kỷ nguyên gần với ngày quan sát. Hiện nay các quan sát thiên văn dùng phương xuân phân của thời đại J2000.0; các dữ liệu cũ hơn dùng B1950.0.

Hướng cơ bản

Hướng cơ bản của một hệ quy chiếu thiên thể là một điểm mốc nằm trên mặt phẳng tham chiếu, cùng với một quy ước chiều dương để tính tọa độ kinh độ; ở hệ tọa độ xích đạo và hệ tọa độ hoàng đạo nó là điểm xuân phân. Trên thực tế điểm hướng mốc không hoàn toàn cố định. Một sự chuyển động chậm của trục Trái đất, gọi là tiến động trục quay hay tuế sai, gây ra sự quay chậm, liên tục của hệ tọa độ về phía tây về các cực hoàng đạo, hoàn thành một vòng quay theo chu kỳ khoảng 26.000 năm. Sự tiến động trục quay còn được tổng hợp với một sự tiến động nhỏ hơn của hoàng đạo, và một sự dao động nhỏ của trục quay Trái Đất gọi là chương động.^[4]

Nhằm cố định vị trí chính xác của điểm mốc hướng cơ bản, các chuyển động này yêu cầu phải chỉ rõ điểm phân của một thời điểm ngày tháng, được gọi là một kỷ nguyên thiên văn, khi đưa ra một vị trí trong hệ tọa độ xích đạo. Ba loại điểm phân thường được sử dụng là:

Điểm phân trung bình của một kỷ nguyên (thường là kỷ nguyên J2000.0, nhưng có thể là B1950.0, B1900.0,...): là một hướng điểm mốc cố định tiêu chuẩn, cho phép các vị trí ở những ngày tháng khác nhau có thể được so sánh trực tiếp.
Điểm phân trung bình của ngày: là giao điểm của hoàng đạo của "ngày" (tức là hoàng đạo ở một vị trí trong một ngày tháng cụ thể) với xích đạo trung bình (tức là, xích đạo được quay tới vị trí hiện tại trong "ngày" đó do tiến động, nhưng không có sự dao động nhỏ theo chu kỳ của chương động). Nó thường được sử dụng trong tính toán quỹ đạo hành tinh.
Điểm phân thực của ngày: là giao điểm của hoàng đạo của "ngày" với xích đạo thực (tức là, xích đạo trung bình cộng với chương động). Đây là giao điểm thật sự của hai mặt phẳng ở mọi thời điểm bất kỳ, với mọi chuyển động đều được tính đến.

Một vị trí trong hệ tọa độ hoàng đạo do đó thường được chỉ rõ, chẳng hạn theo điểm phân thực và hoàng đạo của ngày, điểm phân trung bình và hoàng đạo của J2000.0, hay tương tự. Lưu ý rằng không có "hoàng đạo trung bình", bởi hoàng đạo không có sự dao động nhỏ theo chu kỳ.^[5]

Tọa độ cầu

Tọa độ cầu của một ngôi sao thường được biểu diễn bằng một cặp tọa độ cầu, gọi là xích kinh và xích vĩ, nhưng thường bỏ qua khoảng cách. Hướng của các thiên thể đủ xa được coi là tương tự nhau đối với mọi người quan sát Trái Đất, nên thuận tiện khi chỉ cần xác định hướng này với cùng một tọa độ chung. Ngược lại, trong hệ tọa độ chân trời, vị trí của cùng một ngôi sao là khác nhau đối với những người quan sát ở các vị trí khác nhau của họ trên bề mặt Trái Đất và liên tục thay đổi theo chuyển động quay của Trái Đất.

Kính thiên văn được trang bị giá đỡ xích đạo và các đĩa tròn điều chỉnh sử dụng hệ tọa độ xích đạo để tìm kiếm các thiên thể. Việc thiết lập các đĩa tròn kết hợp với bản đồ sao hoặc lịch thiên văn cho phép kính thiên văn dễ dàng quay và hướng vào các thiên thể đã biết trên thiên cầu.

Xem thêm các bài Xích vĩ và Xích kinh

Xích vĩ

Góc kiểu vĩ độ của hệ tọa độ xích đạo được gọi là xích vĩ (ký hiệu "delta" $δ$ , viết tắt theo tiếng Anh là Dec). Nó là khoảng cách góc giữa vectơ nối tâm Trái Đất với thiên thể (ở phía Bắc hay phía Nam xích đạo thiên cầu) và mặt phẳng xích đạo. Nó có giá trị dương với thiên thể ở phía Bắc xích đạo thiên cầu, và âm với các thiên thể ở phía Nam. Ví dụ, thiên cực Bắc có giá trị xích vĩ +90°. Gốc của xích vĩ là xích đạo thiên cầu, tức là hình chiếu của xích đạo Trái Đất lên thiên cầu. Xích vĩ là khái niệm tương tự với vĩ độ địa lý.^[6]^[7]^[8]

Xích kinh

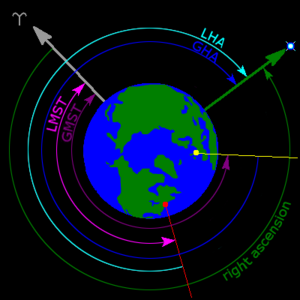
Góc kiểu kinh độ được gọi là xích kinh (ký hiệu "alpha" $α$ , viết tắt theo tiếng Anh là RA). Nó là khoảng cách góc dọc theo xích đạo thiên cầu, giữa vòng giờ đi qua thiên thể và mặt phẳng đi qua thiên cực và điểm xuân phân, tức là một trong hai giao điểm của hoàng đạo với xích đạo thiên cầu. Góc được quy ước có giá trị dương nếu thiên thể nằm ở phương Đông và âm nếu thiên thể nằm ở phương Tây. Khác với xích vĩ và khác với kinh độ, xích kinh thường được đo bằng giờ (phút, giây) thay vì bằng độ, bởi vì sự quay biểu kiến của hệ tọa độ xích đạo gắn chặt với thời gian sao và góc giờ. Một cách đo xích kinh là đo thời gian quá cảnh kinh tuyến của các thiên thể. Vì bầu trời quay trọn một vòng sau 24 giờ, nên một giờ xích kinh bằng 15 độ (360°/24^h = 15°).^[6]^[9]^[10]

Góc giờ

Một tọa độ thay cho xích kinh là góc giờ hay góc giờ địa phương (viết tắt theo tiếng Anh là HA hay LHA, local hour angle), một tọa độ quy ước tay trái, là khoảng cách góc của một thiên thể theo chiều tây dọc theo xích đạo thiên cầu, từ kinh tuyến địa phương của người quan sát tới vòng giờ đi qua thiên thể. Không giống xích kinh, góc giờ luôn tăng với sự quay của Trái Đất. Góc giờ có thể được xem là một cách đo thời gian từ lúc đỉnh điểm trên, thời điểm mà một thiên thể tiếp xúc với kinh tuyến trực tiếp phía trên bầu trời tại nơi người quan sát.

Một ngôi sao tại cực điểm nằm trên kinh tuyến của một người quan sát được gọi là có góc giờ bằng 0 (0h). Một giờ sao (khoảng 0,9973 giờ theo thời gian mặt trời) sau đó, sự tự quay của Trái đất sẽ đưa ngôi sao về phía tây của kinh tuyến, và góc giờ của nó sẽ là 1 giờ. Khi tính toán các hiện tượng trong hệ quy chiếu trên mặt đất, xích kinh có thể được chuyển đổi thành góc giờ như một bước trung gian.^[11]^[12]^[13]

Tọa độ xích đạo mở rộng

Mở rộng thành hệ tọa độ cầu-cực

Với xích kinh và xích vĩ, hệ tọa độ xích đạo chỉ có thể xác định phương tới các thiên thể chứ không thể xác định khoảng cách tới các thiên thể. Để xác định cả khoảng cách tới các thiên thể trong không gian 3 chiều, người ta thêm tọa độ thứ ba, đó là khoảng cách ( $r$ ) từ tâm Trái Đất tới thiên thể. Khi đó hệ tọa độ xích đạo này là hệ tọa độ cầu-cực.

Hệ tọa độ trục vuông góc

Tọa độ xích đạo địa tâm

Có một vài biến thể hệ trục vuông góc của tọa độ xích đạo, và chúng đều có:

Gốc tọa độ đặt tại tâm Trái Đất.
Mặt phẳng cơ bản là mặt phẳng xích đạo Trái Đất.
Hướng cơ bản (hướng của trục $x$ ) là hướng tới điểm xuân phân, tức là, vị trí nơi Mặt Trời cắt qua xích đạo thiên cầu về hướng bắc trong chuyển động biểu kiến chu kỳ hàng năm quanh hoàng đạo.
Quy tắc bàn tay phải, xác định trục $y$ nằm theo hướng về phía đông 90° so với trục $x$ trên mặt phẳng cơ bản và trục $z$ dọc theo trục cực bắc.

Các hệ quy chiếu đều không quay cùng với Trái Đất (trái ngược với các hệ quy chiếu tâm Trái Đất và cố định Trái Đất), luôn hướng tới điểm phân và thay đổi chậm theo thời gian với các chuyển động tiến động và chương động.

Trong thiên văn học:^[14]
- Vị trí của Mặt Trời thường được xác định trong các tọa độ trục vuông góc địa tâm $X$ , $Y$ , $Z$ và một tọa độ thứ tư là khoảng cách $R$ $(= \sqrt X 2 + Y 2 + Z 2)$ , .
- Vị trí của các hành tinh và các thiên thể khác trong hệ Mặt Trời thường được xác định trong các tọa độ vuông góc địa tâm $ξ$ , $η$ , $ζ$ và một tọa độ thứ tư là khoảng cách, $Δ$ (bằng $\sqrt ξ 2 + η 2 + ζ 2$ ), tính bằng đơn vị thiên văn. Các tọa độ vuông góc trên được liên hệ với tọa độ cầu tương ứng theo các công thức
  ${\begin{aligned}{\frac {X}{R}}={\frac {\xi }{\mathit {\Delta }}}&=\cos \delta \cos \alpha \\{\frac {Y}{R}}={\frac {\eta }{\mathit {\Delta }}}&=\cos \delta \sin \alpha \\{\frac {Z}{R}}={\frac {\zeta }{\mathit {\Delta }}}&=\sin \delta \end{aligned}}$
Trong động lực học thiên thể:^[15]
- Vị trí của các vệ tinh Trái Đất nhân tạo được xác định theo tọa độ xích đạo địa tâm, còn gọi là hệ xích đạo địa tâm quán tính (GEI), hệ quán tính địa tâm (ECI), và hệ quán tính quy ước (CIS), tất cả đều tương đương theo định nghĩa với hệ xích đạo vuông góc địa tâm thiên văn ở trên. Trong hệ xích đạo địa tâm, các trục $x$ , $y$ và $z$ còn được viết là $I$ , $J$ và $K$ , tương ứng, hay các cơ sở của hệ được xác định bởi các vectơ đơn vị $Î$ , $Ĵ$ và $K̂$ .
- Hệ quy chiếu Địa tâm Thiên thể (GCRF) là hệ địa tâm tương ứng của Hệ quy chiếu Thiên thể Quốc tế (ICRF). Hướng cơ bản của hệ này là điểm phân của J2000.0, và không di chuyển theo tiến động và chương động, nhưng về mặt khác cũng tương đương với các hệ trên.

Tóm tắt các ký hiệu tọa độ xích đạo thiên văn^[16]
	Tọa độ cầu-cực			Tọa độ trục vuông góc
	Xích kinh	Xích vĩ	Khoảng cách	Tổng quát	Mục đích đặc biệt
Địa tâm	$α$	$δ$	$Δ$	$ξ$ , $η$ , $ζ$	$X$ , $Y$ , $Z$ (của Mặt Trời)
Nhật tâm				$x$ , $y$ , $z$

Tọa độ xích đạo nhật tâm

Trong thiên văn học, một biến thể trục vuông góc nhật tâm của hệ tọa độ xích đạo còn được sử dụng, ký hiệu là $x$ , $y$ , $z$ , và có:

Gốc tọa độ đặt tại tâm Mặt Trời.
Mặt phẳng cơ bản trùng với mặt phẳng xích đạo Trái Đất.
Hướng cơ bản (trục $x$ ) là hướng tới điểm xuân phân.
Quy tắc bàn tay phải xác định trục $y$ nằm theo hướng về phía đông 90° so với trục $x$ trên mặt phẳng cơ bản và trục $z$ dọc theo trục cực bắc của Trái Đất.

Hệ quy chiếu này tương đương với hệ $ξ$ , $η$ , $ζ$ ở trên về mọi mặt, ngoại trừ gốc tọa độ được đặt tại tâm Mặt Trời. Nó thường được sử dụng trong tính toán quỹ đạo hành tinh. Các tọa độ trục vuông góc thiên văn nói trên có liên hệ sau:^[17]

{\begin{aligned}\xi &=x+X\\\eta &=y+Y\\\zeta &=z+Z\end{aligned}}

Mở rộng cho các hành tinh

Hệ tọa độ xích đạo có thể được mở rộng để áp dụng cho các quan sát thiên văn từ hành tinh khác trong hệ Mặt Trời. Chúng cũng sử dụng xích đạo của hành tinh làm mặt phẳng tham chiếu, và điểm xuân phân của hành tinh làm điểm mốc tính kinh độ và vĩ độ. Chúng có thể được gọi với tên chung là hệ tọa độ tâm hành tinh.

Tham khảo

^ Nautical Almanac Office, U.S. Naval Observatory; H.M. Nautical Almanac Office; Royal Greenwich Observatory (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London (reprint 1974). tr. 24, 26.
^ Vallado, David A. (2001). Fundamentals of Astrodynamics and Applications. Microcosm Press, El Segundo, CA. tr. 157. ISBN 1-881883-12-4.
^ U.S. Naval Observatory Nautical Almanac Office; U.K. Hydrographic Office; H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. tr. M2, "apparent place". ISBN 978-0-7077-4082-9.
^ Explanatory Supplement (1961), pp. 20, 28
^ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. tr. 137. ISBN 0-943396-35-2.
^ ^a ^b Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. Cambridge University Press. tr. 28–29. ISBN 0-521-35699-7.
^ Meir H. Degani (1976). Astronomy Made Simple. Doubleday & Company, Inc. tr. 216. ISBN 0-385-08854-X.
^ Astronomical Almanac 2010, p. M4
^ Moulton, Forest Ray (1918). An Introduction to Astronomy. tr. 127.
^ Astronomical Almanac 2010, p. M14
^ Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. Cambridge University Press. tr. 34–36. ISBN 0-521-35699-7.
^ Astronomical Almanac 2010, p. M8
^ Vallado (2001), p. 154
^ Explanatory Supplement (1961), pp. 24–26
^ Vallado (2001), pp. 157, 158
^ Explanatory Supplement (1961), sec. 1G
^ Explanatory Supplement (1961), pp. 20, 27