Một Hệ tọa độ Descartes (tiếng Anh : Cartesian coordinate system ) xác định vị trí của một điểm (point ) trên một mặt phẳng (plane ) cho trước bằng một cặp số tọa độ (x , y ). Trong đó, x và y là 2 giá trị được xác định bởi 2 đường thẳng có hướng vuông góc với nhau (cùng đơn vị đo ). 2 đường thẳng đó gọi là trục tọa độ (coordinate axis ) (hoặc đơn giản là trục ); trục nằm ngang gọi là trục hoành , trục đứng gọi là trục tung ; điểm giao nhau của 2 đường gọi là gốc tọa độ (origin) và nó có giá trị là (0, 0).
Hệ tọa độ này là ý tưởng của nhà toán học và triết học người Pháp René Descartes thể hiện vào năm 1637 trong hai bài viết của ông. Trong phần hai của bài Phương pháp luận (Descartes) (tiếng Pháp : Discours de la méthode , tựa Pour bien conduire sa raison, et chercher la vérité dans les sciences ), ông đã giới thiệu ý tưởng mới về việc xác định vị trí của một điểm hay vật thể trên một bề mặt bằng cách dùng hai trục giao nhau để đo. Còn trong bài La Géométrie , ông phát triển sâu hơn khái niệm trên.
Descartes là người đã có công hợp nhất đại số và hình học Euclide . Công trình này của ông có ảnh hưởng đến sự phát triển của ngành hình học giải tích , tích phân , và khoa học bản đồ .
Ngoài ra, ý tưởng về hệ tọa độ có thể được mở rộng ra không gian ba chiều (three-dimensional space ) bằng cách sử dụng 3 tọa độ Descartes (nói cách khác là thêm một trục tọa độ vào một hệ tọa độ Descartes). Một cách tổng quát, một hệ tọa độ n-chiều có thể được xây dựng bằng cách sử dụng n tọa độ Descartes (tương đương với n-trục).
Là 2 trục vuông góc x'Ox và y'Oy mà trên đó đã chọn 2 vectơ đơn vị
i
→
{\displaystyle {\vec {i}}}
j
→
{\displaystyle {\vec {j}}}
Trục x'Ox (hay trục Ox) gọi là trục hoành.
Trục y'Oy (hay trục Oy) gọi là trục tung.
Điểm O được gọi là gốc tọa độ
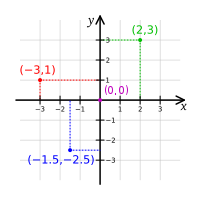
Hình 1 - Hệ tọa độ Đề-Các với bốn điểm lần lượt có tọa độ: (2,3) (màu xanh lá cây) , (-3,1) (màu xanh đỏ) , (-1.5,-2.5) (màu xanh da trời) và (0,0), gốc tọa độ, (màu tím) . Hình 2 - Hệ tọa độ Đề-Các với một đường tròn có tâm trùng với gốc tọa độ và bán kính bằng 2. Đường tròn này có phương trình: x2 + y2 = 4. Hình 3 - Hệ tọa độ Đề-Các với bốn góc phần tư. Các mũi tên ở hai đầu của mỗi trục nhằm minh họa rằng các trục này trải dài vô tận theo hướng của mũi tên.
Nếu
a
→
=
x
i
→
+
y
j
→
{\displaystyle {\vec {a}}=x{\vec {i}}+y{\vec {j}}}
a
→
{\displaystyle {\vec {a}}}
a
→
{\displaystyle {\vec {a}}}
Ký hiệu
a
→
=
(
x
;
y
)
{\displaystyle {\vec {a}}=(x;y)}
Mỗi điểm M được xác định bởi một cặp số M(x,y), được gọi là tọa độ điểm M, x được gọi là hoành độ và y được gọi là tung độ của điểm M
Tính chất:
∀
x
≠
0
,
M
(
x
;
0
)
∈
O
x
{\displaystyle \forall x\neq 0,M(x;0)\in Ox}
∀
y
≠
0
,
M
(
0
;
y
)
∈
O
y
{\displaystyle \forall y\neq 0,M(0;y)\in Oy}
Tọa độ của một điểm chính là tọa độ của vectơ có điểm cuối là điểm đó và điểm đầu là O. Ta có
M
(
x
,
y
)
⇔
O
M
→
=
(
x
;
y
)
{\displaystyle M\left(x,y\right)\Leftrightarrow {\overrightarrow {OM}}=(x;y)}
Cho 2 điểm
A
(
x
A
;
y
A
)
{\displaystyle A(x_{A};y_{A})}
B
(
x
B
;
y
B
)
{\displaystyle B(x_{B};y_{B})}
A
B
→
=
(
x
B
−
x
A
;
y
B
−
y
A
)
{\displaystyle {\overrightarrow {AB}}=\left(x_{B}-x_{A};y_{B}-y_{A}\right)}
Cho
a
→
=
(
a
1
;
a
2
)
{\displaystyle {\vec {a}}=(a_{1};a_{2})}
|
a
→
|
=
a
1
2
+
a
2
2
{\displaystyle \left\vert {\vec {a}}\right\vert ={\sqrt {a_{1}^{2}+a_{2}^{2}}}}
a
→
{\displaystyle {\vec {a}}}
Cho 2 điểm
A
(
x
A
;
y
A
)
{\displaystyle A(x_{A};y_{A})}
B
(
x
B
;
y
B
)
{\displaystyle B(x_{B};y_{B})}
đoạn thẳng AB hay khoảng cách giữa A và B là
A
B
=
(
x
B
−
x
A
)
2
+
(
y
B
−
y
A
)
2
{\displaystyle AB={\sqrt {\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}}}}
Cho
a
→
=
(
a
1
;
a
2
)
{\displaystyle {\vec {a}}=(a_{1};a_{2})}
b
→
=
(
b
1
;
b
2
)
{\displaystyle {\vec {b}}=(b_{1};b_{2})}
α
{\displaystyle \alpha }
a
→
{\displaystyle {\vec {a}}}
b
→
{\displaystyle {\vec {b}}}
cos
α
=
a
1
b
1
+
a
2
b
2
(
a
1
2
+
a
2
2
)
(
b
1
2
+
b
2
2
)
{\displaystyle \cos \alpha ={a_{1}b_{1}+a_{2}b_{2} \over {\sqrt {\left(a_{1}^{2}+a_{2}^{2}\right)\left(b_{1}^{2}+b_{2}^{2}\right)}}}}
Cho
a
→
=
(
a
1
;
a
2
)
{\displaystyle {\vec {a}}=(a_{1};a_{2})}
k
a
→
=
(
k
a
1
;
k
a
2
)
{\displaystyle k{\vec {a}}=(ka_{1};ka_{2})}
Cho
a
→
=
(
a
1
;
a
2
)
{\displaystyle {\vec {a}}=(a_{1};a_{2})}
b
→
=
(
b
1
;
b
2
)
{\displaystyle {\vec {b}}=(b_{1};b_{2})}
a
→
+
b
→
=
(
a
1
+
b
1
;
a
2
+
b
2
)
{\displaystyle {\vec {a}}+{\vec {b}}=(a_{1}+b_{1};a_{2}+b_{2})}
a
→
−
b
→
=
(
a
1
−
b
1
;
a
2
−
b
2
)
{\displaystyle {\vec {a}}-{\vec {b}}=(a_{1}-b_{1};a_{2}-b_{2})}
a
→
.
b
→
=
a
1
b
1
+
a
2
b
2
{\displaystyle {\vec {a}}.{\vec {b}}=a_{1}b_{1}+a_{2}b_{2}}
a
→
{\displaystyle {\vec {a}}}
b
→
{\displaystyle {\vec {b}}}
⇔
{\displaystyle \Leftrightarrow }
a
1
b
2
=
a
2
b
1
{\displaystyle a_{1}b_{2}=a_{2}b_{1}}
Cho đoạn thẳng AB có
A
(
x
A
;
y
A
)
{\displaystyle A(x_{A};y_{A})}
B
(
x
B
;
y
B
)
{\displaystyle B(x_{B};y_{B})}
I
(
x
A
+
x
B
2
;
y
A
+
y
B
2
)
{\displaystyle I\left({x_{A}+x_{B} \over 2};{y_{A}+y_{B} \over 2}\right)}
trung điểm đoạn thẳng AB
Cho
△
A
B
C
{\displaystyle \bigtriangleup ABC}
A
(
x
A
;
y
A
)
{\displaystyle A(x_{A};y_{A})}
B
(
x
B
;
y
B
)
{\displaystyle B(x_{B};y_{B})}
C
(
x
C
;
y
C
)
{\displaystyle C(x_{C};y_{C})}
G
(
x
A
+
x
B
+
x
C
3
;
y
A
+
y
B
+
y
C
3
)
{\displaystyle G\left({x_{A}+x_{B}+x_{C} \over 3};{y_{A}+y_{B}+y_{C} \over 3}\right)}
△
A
B
C
{\displaystyle \bigtriangleup ABC}
Là 3 trục vuông góc nhau từng đôi một x'Ox, y'Oy, z'Oz mà trên đó đã chọn 3 vectơ đơn vị
i
→
{\displaystyle {\vec {i}}}
j
→
{\displaystyle {\vec {j}}}
k
→
{\displaystyle {\vec {k}}}
Trục x'Ox (hay trục Ox) gọi là trục hoành.
Trục y'Oy (hay trục Oy) gọi là trục tung.
Trục z'Oz (hay trục Oz) gọi là trục cao.
Điểm O được gọi là gốc tọa độ
3 trục tọa độ nói trên vuông góc với nhau tạo thành 3 mặt phẳng tọa độ là Oxy, Oyz và Ozx vuộng góc với nhau từng đôi một
Tranh 4 - Hệ tọa độ Descartes ba chiều với trục y có chiều chạy xa người quan sát. Tranh 5 - Hệ tọa độ Descartes ba chiều với trục x có chiều chạy về phía người quan sát.
Tranh 6 - The left-handed orientation is shown on the left, and the right-handed on the right. Tranh 7 - The right-handed Cartesian coordinate system indicating the coordinate planes.
Trong không gian, mỗi điểm M được xác định bởi bộ số M(x,y,z). và ngược lại, bộ số đó được gọi là tọa độ của điểm M, x được gọi là hoành độ, y được gọi là tung độ và z được gọi là cao độ của điểm M.
Tính chất
∀
x
y
≠
0
,
A
(
x
,
y
,
0
)
∈
O
x
y
{\displaystyle \forall xy\neq 0,A(x,y,0)\in Oxy}
∀
x
z
≠
0
,
A
(
x
,
0
,
z
)
∈
O
x
z
{\displaystyle \forall xz\neq 0,A(x,0,z)\in Oxz}
∀
y
z
≠
0
,
A
(
0
,
y
,
z
)
∈
O
y
z
{\displaystyle \forall yz\neq 0,A(0,y,z)\in Oyz}
∀
x
≠
0
,
M
(
x
;
0
;
0
)
∈
O
x
{\displaystyle \forall x\neq 0,M(x;0;0)\in Ox}
∀
y
≠
0
,
M
(
0
;
y
;
0
)
∈
O
y
{\displaystyle \forall y\neq 0,M(0;y;0)\in Oy}
∀
z
≠
0
,
M
(
0
;
0
;
z
)
∈
O
z
{\displaystyle \forall z\neq 0,M(0;0;z)\in Oz}
Trong không gian, cho vectơ
a
→
=
x
i
→
+
y
j
→
+
z
k
→
{\displaystyle {\vec {a}}=x{\vec {i}}+y{\vec {j}}+z{\vec {k}}}
a
→
{\displaystyle {\vec {a}}}
Ký hiệu:
a
→
=
(
x
;
y
;
z
)
{\displaystyle {\vec {a}}=(x;y;z)}
Cho 2 điểm
A
(
x
A
;
y
A
;
z
A
)
{\displaystyle A(x_{A};y_{A};z_{A})}
B
(
x
B
;
y
B
;
z
B
)
{\displaystyle B(x_{B};y_{B};z_{B})}
A
B
→
=
(
x
B
−
x
A
;
y
B
−
y
A
;
z
B
−
z
A
)
{\displaystyle {\overrightarrow {AB}}=\left(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A}\right)}
Cho điểm
M
(
x
M
;
y
M
;
z
M
)
{\displaystyle M(x_{M};y_{M};z_{M})}
O
M
→
=
(
x
M
;
y
M
;
z
M
)
{\displaystyle {\vec {OM}}=(x_{M};y_{M};z_{M})}
Cho
a
→
=
(
a
1
;
a
2
;
a
3
)
{\displaystyle {\vec {a}}=(a_{1};a_{2};a_{3})}
|
a
→
|
=
a
1
2
+
a
2
2
+
a
3
2
{\displaystyle \left\vert {\vec {a}}\right\vert ={\sqrt {a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}}}
a
→
{\displaystyle {\vec {a}}}
Cho 2 điểm
A
(
x
A
;
y
A
;
z
A
)
{\displaystyle A(x_{A};y_{A};z_{A})}
B
(
x
B
;
y
B
;
z
B
)
{\displaystyle B(x_{B};y_{B};z_{B})}
A
B
=
(
x
B
−
x
A
)
2
+
(
y
B
−
y
A
)
2
+
(
z
B
−
z
A
)
2
{\displaystyle AB={\sqrt {(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}}}
Cho
a
→
=
(
a
1
;
a
2
;
a
3
)
{\displaystyle {\vec {a}}=(a_{1};a_{2};a_{3})}
b
→
=
(
b
1
;
b
2
;
b
3
)
{\displaystyle {\vec {b}}=(b_{1};b_{2};b_{3})}
α
{\displaystyle \alpha }
a
→
{\displaystyle {\vec {a}}}
b
→
{\displaystyle {\vec {b}}}
cos
(
α
)
=
a
→
.
b
→
|
a
→
|
|
b
→
|
=
a
1
b
1
+
a
2
b
2
+
a
3
b
3
(
a
1
2
+
a
2
2
+
a
3
2
)
(
b
1
2
+
b
2
2
+
b
3
2
)
{\displaystyle \cos(\alpha )={{\vec {a}}.{\vec {b}} \over \left\vert {\vec {a}}\right\vert \left\vert {\vec {b}}\right\vert }={a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3} \over {\sqrt {(a_{1}^{2}+a_{2}^{2}+a_{3}^{2})(b_{1}^{2}+b_{2}^{2}+b_{3}^{2})}}}}
sin
α
=
|
[
a
→
;
b
→
]
|
|
a
→
|
|
b
→
|
{\displaystyle \sin \alpha ={\left\vert [{\vec {a}};{\vec {b}}]\right\vert \over \left\vert {\vec {a}}\right\vert \left\vert {\vec {b}}\right\vert }}
Cho
a
→
=
(
a
1
;
a
2
;
a
3
)
{\displaystyle {\vec {a}}=(a_{1};a_{2};a_{3})}
k
a
→
=
(
k
a
1
;
k
a
2
;
k
a
3
)
{\displaystyle k{\vec {a}}=(ka_{1};ka_{2};ka_{3})}
Cho
a
→
=
(
a
1
;
a
2
;
a
3
)
{\displaystyle {\vec {a}}=(a_{1};a_{2};a_{3})}
b
→
=
(
b
1
;
b
2
;
b
3
)
{\displaystyle {\vec {b}}=(b_{1};b_{2};b_{3})}
a
→
+
b
→
=
(
a
1
+
b
1
;
a
2
+
b
2
;
a
3
+
b
3
)
{\displaystyle {\vec {a}}+{\vec {b}}=(a_{1}+b_{1};a_{2}+b_{2};a_{3}+b_{3})}
a
→
−
b
→
=
(
a
1
−
b
1
;
a
2
−
b
2
;
a
3
−
b
3
)
{\displaystyle {\vec {a}}-{\vec {b}}=(a_{1}-b_{1};a_{2}-b_{2};a_{3}-b_{3})}
a
→
.
b
→
=
a
1
b
1
+
a
2
b
2
+
a
3
b
3
{\displaystyle {\vec {a}}.{\vec {b}}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}
[
a
→
,
b
→
]
=
(
|
a
2
a
3
b
2
b
3
|
;
|
a
3
a
1
b
3
b
1
|
;
|
a
1
a
2
b
1
b
2
|
)
{\displaystyle \left[{\vec {a}},{\vec {b}}\right]={\big (}{\begin{vmatrix}a_{2}&a_{3}\\b_{2}&b_{3}\end{vmatrix}};{\begin{vmatrix}a_{3}&a_{1}\\b_{3}&b_{1}\end{vmatrix}};{\begin{vmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{vmatrix}})}
Cho đoạn thẳng AB có
A
(
x
A
;
y
A
;
z
A
)
{\displaystyle A(x_{A};y_{A};z_{A})}
B
(
x
B
;
y
B
;
z
B
)
{\displaystyle B(x_{B};y_{B};z_{B})}
I
(
x
A
+
x
B
2
;
y
A
+
y
B
2
;
z
A
+
z
B
2
)
{\displaystyle I\left({x_{A}+x_{B} \over 2};{y_{A}+y_{B} \over 2};{z_{A}+z_{B} \over 2}\right)}
Cho
△
A
B
C
{\displaystyle \bigtriangleup ABC}
A
(
x
A
;
y
A
;
z
A
)
{\displaystyle A(x_{A};y_{A};z_{A})}
B
(
x
B
;
y
B
;
z
B
)
{\displaystyle B(x_{B};y_{B};z_{B})}
C
(
x
C
;
y
C
;
z
C
)
{\displaystyle C(x_{C};y_{C};z_{C})}
G
(
x
A
+
x
B
+
x
C
3
;
y
A
+
y
B
+
y
C
3
;
z
A
+
z
B
+
z
C
3
)
{\displaystyle G\left({x_{A}+x_{B}+x_{C} \over 3};{y_{A}+y_{B}+y_{C} \over 3};{z_{A}+z_{B}+z_{C} \over 3}\right)}
△
A
B
C
{\displaystyle \bigtriangleup ABC}
Sách giáo khoa Toán 7 tập 1Sách giáo khoa Hình học lớp 10
Sách giáo khoa Hình học lớp 10 nâng cao
Sách giáo khoa Hình học lớp 12
Sách giáo khoa Hình học lớp 12 nâng cao
![{\displaystyle \sin \alpha ={\left\vert [{\vec {a}};{\vec {b}}]\right\vert \over \left\vert {\vec {a}}\right\vert \left\vert {\vec {b}}\right\vert }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2910d5b647b60cec16f1fd710404a3c4a9bcb73)
![{\displaystyle \left[{\vec {a}},{\vec {b}}\right]={\big (}{\begin{vmatrix}a_{2}&a_{3}\\b_{2}&b_{3}\end{vmatrix}};{\begin{vmatrix}a_{3}&a_{1}\\b_{3}&b_{1}\end{vmatrix}};{\begin{vmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{vmatrix}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75c5f379d8c759bec8472dfc1ad67d153e5761d4)
GIẢM
33%
GIẢM
50%
![[Review] Đường Mây Qua Xứ Tuyết: Điểm giống và khác giữa Phật giáo Tây Tạng với Phật giáo Việt Nam](https://down-bs-vn.img.susercontent.com/d582778a882305f006031617fc0a69d5.webp)
![[Review Sách] Đọc vị tâm trí](https://down-bs-vn.img.susercontent.com/sg-11134201-7qvdk-libws1cgh4ks57.webp)
GIẢM
20%
GIẢM
34%
![[Review sách] Xá lợi toàn thân - Bài Pháp Vô Ngôn](https://down-bs-vn.img.susercontent.com/sg-11134201-7rble-lluxxe4d8mzd69.webp)
GIẢM
20%
