Mặt (tô pô)

Đối với các định nghĩa khác, xem mặt.

Mặt yên ngựa (mặt hyperbolic paraboloid).

Chai Klein trong không gian 3 chiều.

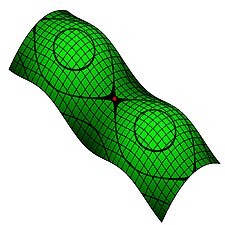
Trong toán học, cụ thể là trong topo, một mặt là một đa tạp topo 2 chiều. Ví dụ quen thuộc nhất về mặt chính là phần biên của các khối trong không gian Euclid 3 chiều thông thường, chẳng hạn như mặt cầu. Ngoài ra, cũng có những mặt, chẳng hạn như chai Klein, không thể được nhúng vào không gian Euclid 3 chiều mà không sử dụng kỳ dị hoặc tự cắt.

Một mặt là "2 chiều" nghĩa là tại mỗi điểm, ta có thể xác định được một hệ tọa độ 2 chiều trên mặt. Chẳng hạn, với bề mặt Trái Đất, mà ta giả sử là một mặt cầu 2 chiều, thì các đường kinh tuyến và vĩ tuyến tạo thành một hệ trục tọa độ trên mặt cầu, trừ hai cực và kinh tuyến gốc.

Khái niệm mặt cũng được sử dụng trong vật lý, kỹ thuật, xử lý hình ảnh và nhiều lĩnh vực khác. Chẳng hạn, việc phân tích khí động học của một máy bay tập trung vào dòng chảy của không khí qua các mặt.

Định nghĩa và ví dụ

Một mặt (topo) là một không gian topo Hausdorff khác rỗng và có cơ sở đếm được, trong đó mọi điểm đều có một lân cận mở đồng phôi với một tập mở của không gian Euclid 2 chiều. Các lân cận này, cùng với các đồng phôi tương ứng, được gọi là một hệ tọa độ (coordinate chart). Nhờ chúng mà các lân cận giữ được hệ trục tọa độ chuẩn tắc trên mặt phẳng Euclid. Do đó, mặt được gọi là có tính Euclid địa phương.

Tổng quát hơn, một mặt (topo) có biên là một không gian topo Hausdorff mà trên đó mỗi điểm có một lân cận mở đồng phôi với một tập mở nào đó trong nửa mặt phẳng trên đóng trong ${\displaystyle \mathbb {R} ^{2}}$

Các đồng phôi này cũng được gọi là hệ tọa độ địa phương. Biên của nửa mặt phẳng trên chính là trục hoành. Các điểm trên mặt tương ứng một điểm trên trục hoành qua một trong số các phép đồng phôi nói trên thì được gọi là điểm biên của mặt. Các điểm biên này lập thành biên của mặt và là một đa tạp 1 chiều không có biên, tức là hội của các đường cong đóng. Các điểm của mặt tương ứng với các điểm không nằm trong trục hoành được gọi là điểm trong. Tập hợp các điểm trong được gọi là phần trong của mặt và luôn khác rỗng. Ví dụ đơn giản nhất về một mặt có biên là các dĩa tròn đóng. Phần biên của chúng chính là các đường tròn.

Nếu không nói gì thêm, một mặt thường được hiểu là một mặt không có biên. Cụ thể, một mặt có biên bằng rỗng chính là mặt theo nghĩa thông thường. Một mặt compact, biên rỗng được gọi là một mặt 'đóng'. Các mặt cầu, mặt xuyến 2 chiều và các mặt chiếu thực là những ví dụ về mặt đóng.

Dải Mobius là mặt chỉ có một phía. Một cách tổng quát, một mặt được gọi là định hướng được nếu nó không chứa một đồng phôi của dải Mobius; một cách cảm tính, nó có hai phía phân biệt. Mặt cầu và mặt xuyến là những mặt định hướng được, trong khi đó mặt chiếu thực thì không vì khi xóa đi một điểm hoặc một dĩa tròn khỏi mặt chiếu thực, ta thu được dải Mobius

Trong hình học vi phân và hình học đại số, các cấu trúc khác được thêm vào topo của mặt, việc này giúp nhận ra các kỳ dị, chẳng hạn như các điểm tự cắt, cusps, việc mà ta không thể làm được thuần túy dưới ngôn ngữ topo.

Định nghĩa ngoại hàm của mặt và phép nhúng

Mặt cầu được định nghĩa bằng tham số hóa (x = r sin θ cos φ, y = r sin θ sin φ, z = r cos θ) hoặc định nghĩa ẩn (x² + y² + z² − r² = 0.)

Mặt ban đầu được định nghĩa là một không gian con của trong không gian Euclide, mà thông thường, những mặt này là các không điểm (tập nghiệm) của các hàm đa thức. Vì vậy, người ta gọi cách định nghĩa mặt này có tính ngoại hàm.

Trong mục trước, một mặt được định nghĩa bởi một không gian topo có tính chất Hausdorff và Euclide địa phương. Không gian topo này không cần xét là một không gian con của một không gian khác. Cách định nghĩa này có tính nội tại, và hiện nay Toán học dùng cách định nghĩa này để thấy rõ cấu trúc topo nội tại của mặt.

Một mặt được định nghĩa nội tại thì không có thêm sự ràng buộc với vai trò là không gian con của một không gian Euclide. Điều này làm cho các mặt được định nghĩa nội tại có vẻ không phải là một mặt với cấu trúc ngoại hàm (được định nghĩa trong không gian Euclide). Tuy nhiên, định lý nhúng Whitney khẳng định rằng mọi mặt đều có thể nhúng đồng phôi vào một không gian Euclide, trong không gian E⁴: Cách định nghĩa ngoại hàm và nội tại là tương đương với nhau.

Mọi mặt compact có định hướng được hoặc có biên đều có thể nhúng vô E³; mặt khác, một mặt phẳng thực xạ ảnh, compact, không định hướng được và không có biên, thì không thể nhúng vô E³. Mặt Steiner, bao gồm mặt Boy, mặt Roman và cross-cap, là ảnh nhúng chìm của không gian xạ ảnh thực trong E³.

Một dạng thắt nút của mặt xuyến.

Mỗi cách nhúng mặt vô một không gian khác (nếu có nhiều cách) cho ta một thông tin ngoại hàm khác nhau. Ví dụ, mặt xuyến có thể nhúng vào E³ một cách thông thường (giống chiếc nhẫn) hoặc thắt nút (xem hình). Hai cách nhúng là đồng phôi với nhau, nhưng không tương đương đồng luân.

Ảnh của ánh xạ liên tục, đơn ánh từ R² vào không gian nhiều chiều Rⁿ được gọi là một mặt tham số. Một mặt tham số không nhất thiết là mặt topo.

Xây dựng mặt từ đa giác

Mọi mặt đóng đều có thể được xây dựng từ một hình đa giác có số chẵn các cạnh và các cạnh này được định hướng. Đa giác như vậy, gọi là đa giác cơ bản của mặt, tạo nên mặt bằng cách đồng nhất (dán) các cặp cạnh của nó lại. Trong các ví dụ dưới đây, nếu dán các cạnh của đa giác lại với nhau sao cho chúng đúng tên (A với A, B với B) và đúng hướng (được thể hiện bằng các mũi tên) sẽ tạo thành các mặt tương ứng.

• 
  Mặt cầu
• 
  Mặt phẳng xạ ảnh (real projective plane ${\displaystyle \mathbb {R} P^{2}}$
• 
  Mặt xuyến (torus)
• 
  Chai Klein

Mọi đa giác cơ bản đều có thể viết được dưới dạng ký hiệu như sau. Bắt đầu từ một đỉnh, tiến hành di chuyển trên các cạnh của đa giác theo một chiều xác định (có thể là thuận hoặc ngược chiều kim đồng hồ) đến khi trở lại điểm ban đầu. Trong lúc di chuyển, ghi lại tên các cạnh, trong đó thêm số mũ là -1 nếu đang di chuyển ngược định hướng của cạnh đó. Bốn hình trên, khi cuất phát từ góc trái-trên và di chuyển ngược chiều kim đồng hồ, ta thu được

• Mặt cầu: ${\displaystyle ABB^{-1}A^{-1}}$
• Mặt phẳng xạ ảnh: ${\displaystyle ABAB}$
• Mặt xuyến: ${\displaystyle ABA^{-1}B^{-1}}$
• Chai Klein: ${\displaystyle ABAB^{-1}}$.

Việc dán các cạnh của đa giác là một trường hợp đặc biệt của việc xây dựng không gian thương. Một cách tổng quát hơn, khái niệm không gian thương có thể được dùng để xây dựng các mặt. Chẳng hạn, khi xét thương của mặt cầu khi được đồng nhất tất cả các điểm đối xứng với nhau qua tâm (antipodes), ta thu được mặt phẳng xạ ảnh thực. Một ví dụ khác của phép lấy thương là tổng trực tiếp.

Tổng trực tiếp của hai mặt

Tổng trực tiếp của hai mặt M và N, ký hiệu M # N, là mặt nhận được khi cắt đi từ mỗi mặt này một dĩa tròn và dán phần biên (là những đường tròn) của chúng lại với nhau. Đặc trưng Euler của tổng trực tiếp bằng tổng đặc trưng Euler của các số hạng trừ đi 2.

${\displaystyle \chi (M\#N)=\chi (M)+\chi (N)-2.\,}$

Mặt cầu S là phần tử đơn vị của phép lấy tổng trực tiếp, nghĩa là S # M = M. Điều này là vì mặt cầu khi xóa đi một dĩa tròn thì cũng là một dĩa tròn nên khi thực hiện phép dán, nó thay thế cho dĩa tròn đã bị cắt từ M

Việc lấy tổng trực tiếp của một mặt M với mặt xuyến T có thể được xem như để lại trên M một lỗ tròn. Nếu M là một mặt định hướng được thì T # M cũng định hướng được. Vì tổng trực tiếp là phép toán giao hoán nên tổng trực tiếp của hữu hạn các mặt cũng được xác định tốt.

Tổng trực tiếp của hai mặt phẳng xạ ảnh, P # P, là chai Klein K. Tổng trực tiếp của mặt phẳng xạ ảnh và chai Klein thì đồng phôi với tổng trực tiếp của mặt phẳng xạ ảnh và mặt xuyến; nói cách khác, ta có công thức P # K = P # T. Do đó, tổng trực tiếp của 3 mặt phẳng xạ ảnh thì đồng phôi với tổng trực tiếp của mặt phẳng xạ ảnh và mặt xuyến. Khi có một số hạng là mặt phẳng xạ ảnh thì tổng trực tiếp là một mặt không định hướng được.

Mặt đóng

Một mặt đóng là một mặt compact không có biên. Ví dụ về những mặt đóng là mặt cầu, mặt xuyến và chai Klein. Ví dụ về những mặt không đóng là dĩa tròn (là mặt cầu bỏ đi một điểm), mặt trụ (là mặt cầu bỏ đi hai điểm) và dải Mobius

Định lý phân loại mặt đóng

Ví dụ về các mặt đóng định hướng được (bên trái) và các mặt có biên (bên phải). Bên trái: mặt cầu, mặt xuyến, mặt của khối lập phương (đồng phôi với mặt cầu). Bên phải: dĩa tròn, hình vuông, mặt bán cầu (hemisphere). Biên của các mặt được vẽ màu đó. Các mặt này đều đồng phôi với nhau.

Định lý phân loại mặt đóng phát biểu rằng: Mọi mặt đóng và liên thông thì đồng phôi với một phần tử trong các họ sau:

1. Mặt cầu;
2. Tổng trực tiếp của g mặt xuyến, với ${\displaystyle g\geq 1}$;
3. Tổng trực tiếp của k mặt phẳng xạ ảnh, for ${\displaystyle k\geq 1}$.

Các mặt thuộc hai họ đầu tiên thì định hướng được. Ta cũng có thể gộp hai họ này là một bằng cách xem mặt cầu là tổng trực tiếp của 0 mặt xuyến. Số mặt xuyến g được gọi là giống (genus) của mặt. Đặc trưng Euler của mặt cầu và mặt xuyến lần lượt là 2 và 0 và một cách tổng quát, đặc trưng Euler của tổng trực tiếp g mặt xuyến là 2 − 2g.

Các mặt thuộc họ thứ ba thì không định hướng được. Đặc trưng Euler của mặt phẳng xạ ảnh là 1, do đó, đặc trưng Euler của tổng trực tiếp k mặt phẳng xạ ảnh là 2 − k.

Từ hai điều trên, có thể thấy một mặt đóng sẽ xác định duy nhất, sai khác một đồng phôi, với 2 thông tin sau: đặc trưng Euler và việc nó có định hướng được hay không. Nói cách khác, đặc trưng Euler và tính định hướng được hoàn toàn phân loại, sai khác một đồng phôi, được các mặt đóng.

Mặt đóng gồm nhiều thành phần liên thông cũng có thể được phân loại bằng việc phân loại từng thành phần liên thông của nó. Do đó sẽ không mất tính tổng quát nếu ta giả sử mặt là liên thông.

Xem Thêm

• Mặt Riemann
• Định lý Gauss-Bonnet

Tham khảo

Liên kết ngoài

• Mặt (tô pô) tại Từ điển bách khoa Việt Nam
• “Point”. PlanetMath.

(tiếng Mỹ)

• Weisstein, Eric W., "Surface" từ MathWorld. (tiếng Mỹ)

Các chủ đề chính trong toán học
Nền tảng toán học | Đại số | Giải tích | Hình học | Lý thuyết số | Toán học rời rạc | Toán học ứng dụng | Toán học giải trí | Toán học tô pô | Xác suất thống kê