Robert Recorde

Robert Recorde
Robert Recorde
	Robert Recorde (c.1512–1558)
Sinh	k. 1512; Tenby, Pembrokeshire, xứ Wales
Mất	1558; London, Anh
Quốc tịch	Xứ Wales
Trường lớp	Đại học Oxford; Đại học Cambridge
Nổi tiếng vì	Người phát minh ra dấu bằng(=)
	Sự nghiệp khoa học
Ngành	Bác sĩ và toán học
Nơi công tác	Đại học Oxford; Royal Mint

Robert Recorde (1512 - 1558) là một bác sĩ và nhà toán học người xứ Wales. Ông đã phát minh ra dấu bằng^{[cần dẫn nguồn]} (=) và cũng đã giới thiệu dấu cộng (+) đã có từ trước cho người nói tiếng Anh vào năm 1557.

Tiểu sử

Robert Recorde sinh vào khoảng năm 1512, là con trai thứ hai của Thomas và Rose Recorde ở Tenby, Pembrokeshire, xứ Wales.^[1]

Recorde vào Đại học Oxford khoảng năm 1525, và được bầu làm thành viên của Đại học All Souls năm 1531. Năm 1545, ông đến Đại học Cambridge để lấy bằng Bác sĩ. Sau đó, ông trở lại Oxford, nơi ông công khai giảng dạy toán học, như ông đã làm trước khi đến Cambridge. Có vẻ như sau đó ông đã đến London, và làm bác sĩ cho Vua Edward VI và cho Nữ hoàng Mary, người đã dành một số cuốn sách của ông. Ông cũng là người điều khiển Xưởng đúc tiền Hoàng gia và từng là Người kiểm soát Mỏ và Đồng tiền ở Ireland.^[2] Sau khi bị một kẻ thù chính trị kiện vì tội phỉ báng, ông bị bắt vì nợ nần và chết trong nhà tù King's Bench, Southwark, vào giữa tháng 6 năm 1558.

Xuất bản

Phương trình đầu tiên được biết đến, tương đương với 14 x + 15 = 71 trong phương trình hiện đại.

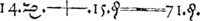
Recorde đã xuất bản một số công trình về các chủ đề toán học và y học, chủ yếu dưới hình thức đối thoại giữa thạc sĩ và học giả, chẳng hạn như sau:

The Grounde of Artes, dạy giá trị và thực hành, của số học, cả số nguyên và phân số (1543),^[1] cuốn sách tiếng Anh đầu tiên về đại số .
Con đường dẫn đến tri thức, chứa đựng những Nguyên tắc đầu tiên của Hình học ... bothe để sử dụng Công cụ Geometricall và Astronomicall, và cả cho Phép chiếu Plattes (London, 1551)
Lâu đài của tri thức, chứa đựng sự Explication của Sphere cả Celestiall và Materiall, v.v. (London, 1556) Một cuốn sách giải thích thiên văn học Ptolemaic trong khi đề cập đến mô hình nhật tâm Copernic khi đi qua.
Whetstone của Witte, được coi là parte thứ hai của Arithmeteke: chứa phần chiết rễ; thực hành giống nhau, với quy tắc của phương trình; và các tác phẩm của Surde Nombers (London, 1557). Đây là cuốn sách trong đó dấu bằng được giới thiệu. Với việc xuất bản cuốn sách này, Recorde được ghi nhận là người đưa đại số vào Đảo Anh với một ký hiệu có hệ thống.^[3]^[4]
Một tác phẩm y học, The Urinal of Physick (1548), thường xuyên được tái bản.^[5]

Ông được cho là tác giả (không rõ) của một số cuốn sách : Cosmographiae isagoge, De Arte faciendi Horologium và De Usu Globorum et de Statu temporum.^[6]

Xem thêm

Chú thích

^ ^a ^b Johnston, Stephen (2004). “Recorde, Robert (c. 1512–1558)”. Oxford Dictionary of National Biography. Oxford University Press. doi:10.1093/ref:odnb/23241. Truy cập ngày 26 tháng 1 năm 2012.
^ Newman, James R. (1956). The World of Mathematics.
^ Jourdain, Philip E. B. (1913). The Nature of Mathematics.
^ Robert Recorde, The Whetstone of Witte (London, England: John Kyngstone, 1557), p. 236 (although the pages of this book are not numbered). From the chapter titled "The rule of equation, commonly called Algebers Rule" (p. 236): "Howbeit, for easie alteration of equations. I will propounde a fewe examples, bicause the extraction of their rootes, maie the more aptly bee wroughte. And to avoide the tediouse repetition of these woordes: is equalle to: I will sette as I doe often in worke use, a paire of paralleles, or Gemowe [twin, from gemew, from the French gemeau (twin / twins), from the Latin gemellus (little twin)] lines of one lengthe, thus: =, bicause noe .2. thynges, can be moare equalle." (However, for easy manipulation of equations, I will present a few examples in order that the extraction of roots may be more readily done. And to avoid the tedious repetition of these words "is equal to", I will substitute, as I often do when working, a pair of parallels or twin lines of the same length, thus: =, because no two things can be more equal.)
^ The Urinal of Physick, by Robert Recorde, 1548; at Google Books
^ John Hall, "An Historiall Expostulation", p. 60. In Early English Poetry, Ballads, and Popular Literature of the Middle Ages, v. XI. London: T. Richards, 1844

Nguồn

Bài viết này bao gồm văn bản từ một ấn phẩm hiện thời trong phạm vi công cộng: Chisholm, Hugh biên tập (1911). “Recorde, Robert”. Encyclopædia Britannica. 22 (ấn bản thứ 11). Cambridge University Press. tr. 966.
James R. Newman (1956). The World of Mathematics Vol. 1 Commentary on Robert Recorde
Philip E. B. Jourdain (1913). The Nature of Mathematics
Gareth Roberts and Fenny Smith, editors (2012). Robert Recorde: The Life and Times of a Tudor Mathematician (University of Wales Press, distributed by University of Chicago Press) 232 pages
Jack Williams (2011). Robert Recorde: Tudor Polymath, Expositor and Practitioner of Computation (Heidelberg, Springer) (History of Computing).
J. W. S. Cassels (1976). Is This a Recorde?, The Mathematical Gazette Vol. 60 No. 411 March 1976 p 59-61
Gordon Roberts (2016). Robert Recorde: Tudor Scholar and Mathematician (University of Wales Press).
Frank J. Swetz and Victor J. Katz (2011). "Mathematical Treasures - Robert Recorde's Whetstone of Witte," Convergence (January 2011) Lưu trữ 2022-09-20 tại Wayback Machine

Liên kết ngoài

Tiểu sử Lịch sử Toán học Đại học St. Andrew
Robert Recorde và các nhà Toán học xứ Wales khác
100 anh hùng xứ Wales - Robert Recorde
Sử dụng sớm nhất các biểu tượng của mối quan hệ
Công dụng được biết đến nhiều nhất của một số từ ngữ trong toán học Điều này có chứa nhiều trích dẫn từ Recorde.
RECORDE (Robert) trong Từ điển Toán học và Triết học của Charles Hutton^{[liên kết hỏng]}
Robert Recorde's life and works on h2g2
Nhà xuất bản hiện tại của Robert Recorde sách của Robert Recorde ở dạng tái bản gốc Lưu trữ 2016-11-05 tại Wayback Machine
Works by Robert Record
Works by or about Robert Recorde

[ODNB-1] Johnston, Stephen (2004). “Recorde, Robert (c. 1512–1558)”. Oxford Dictionary of National Biography. Oxford University Press. doi:10.1093/ref:odnb/23241. Truy cập ngày 26 tháng 1 năm 2012.

[2] Newman, James R. (1956). The World of Mathematics.

[3] Jourdain, Philip E. B. (1913). The Nature of Mathematics.

[4] Robert Recorde, The Whetstone of Witte (London, England: John Kyngstone, 1557), p. 236 (although the pages of this book are not numbered). From the chapter titled "The rule of equation, commonly called Algebers Rule" (p. 236): "Howbeit, for easie alteration of equations. I will propounde a fewe examples, bicause the extraction of their rootes, maie the more aptly bee wroughte. And to avoide the tediouse repetition of these woordes: is equalle to: I will sette as I doe often in worke use, a paire of paralleles, or Gemowe [twin, from gemew, from the French gemeau (twin / twins), from the Latin gemellus (little twin)] lines of one lengthe, thus: =, bicause noe .2. thynges, can be moare equalle." (However, for easy manipulation of equations, I will present a few examples in order that the extraction of roots may be more readily done. And to avoid the tedious repetition of these words "is equal to", I will substitute, as I often do when working, a pair of parallels or twin lines of the same length, thus: =, because no two things can be more equal.)

[5] The Urinal of Physick, by Robert Recorde, 1548; at Google Books

[6] John Hall, "An Historiall Expostulation", p. 60. In Early English Poetry, Ballads, and Popular Literature of the Middle Ages, v. XI. London: T. Richards, 1844

[1]

[2]

[3]

[4]

[5]

[6]

Robert Recorde
Robert Recorde (c.1512–1558)
Sinh	k. 1512 Tenby, Pembrokeshire, xứ Wales
Mất	1558 (1558) London, Anh
Quốc tịch	Xứ Wales
Trường lớp	Đại học Oxford Đại học Cambridge
Nổi tiếng vì	Người phát minh ra dấu bằng(=)
Sự nghiệp khoa học
Ngành	Bác sĩ và toán học
Nơi công tác	Đại học Oxford Royal Mint