Số Bell

Trong toán học tổ hợp, số Bell đếm số phân hoạch của tập hợp. Các số này được nghiên cứu bởi các nhà toán học từ thế kỷ 19, và nguồn gốc bắt đầu từ thời trung cổ Nhật Bản. Là ví dụ của luật eponymy của Stigler, chúng được đặt tên theo Eric Temple Bell, người viết về các số này trong những năm 1930.

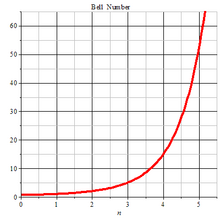
Các số Bell thường được ký hiệu là B_n, trong đó n là số nguyên lớn hơn hoặc bằng 0. Bắt đầu với B₀ = B₁ = 1,các số Bell đầu tiên là

1, 1, 2, 5, 15, 52, 203, 877, 4140, ... (dãy số A000110 trong bảng OEIS).

Số Bell B_n đếm số cách khác nhau để phân hoạch tập hợp có n phần tử,hoặc tương đương là số quan hệ tương đương trên tập đó. Ngoài ra B_n cũng đếm số lược đồ vần cho bài thơ có n dòng.^[1]

Ngoài việt xuất hiện trong các bài toán đếm, các số này còn có ý nghĩa khác như là mô men của các phân phối xác suất. Cụ thể hơn , B_n là mô men thứ n của phân phối Poisson với số bình quân bằng 1.

Bài toán đếm

Phân hoạch của một tập hợp

Tổng quát, B_n là số các phân hoạch của tập hợp kích thước n. Phân hoạch của tập S là một họ các tập con không rỗng, rời nhau mà hợp của chúng bằng S.

Chẳng hạn, B₃ = 5 vì tập hợp ba phần tử {a, b, c} có thể phân hoạch theo 5 cách khác nhau:

{ {a}, {b}, {c} }

{ {a}, {b, c} }

{ {b}, {a, c} }

{ {c}, {a, b} }

{ {a, b, c} }.

B₀ là 1 vì có đúng một phân hoạch của tập rỗng. Đây là trường hợp đặc biệt, đối với n >0 sẽ không xét tập con rỗng.

Chú ý rằng, trong mệnh đề trên chúng ta không phân biệt các thành phần của một phân hoạch. Như vậy các cách viết sau chỉ cùng một phân hoạch:

{ {b}, {a, c} }

{ {a, c}, {b} }

{ {b}, {c, a} }

{ {c, a}, {b} }

Đếm hoán vị

Các số Bell cũng có thể xem như số các khả năng khác nhau đặt n quả bóng vào một hoặc nhiều hộp. Chẳng hạn với n = 3, ta có ba quả bóng được ghi nhãn a, b, and c, và ba hộp. Nếu không phân biệt thứ tự các hộp ta có năm cách phân phối:

Mỗi quả bóng vào một hộp
Tất cả ba quả bóng vào một hộp.
a vào một hộp; b và c vào một hộp khác.
b vào một hộp; a và c vào một hộp khác.
c vào một hộp; b và a vào một hộp khác.

Tính chất của các số Bell

Công thức truy hồi:

B_{n+1}=\sum _{k=0}^{n}{{n \choose k}B_{k}}.

Chúng thoả mãn "Công thức Dobinski":

B_{n}={\frac {1}{e}}\sum _{k=0}^{\infty }{\frac {k^{n}}{k!}}=

là momen thứ n của phân phối Poisson với kỳ vọng bằng 1.

Chúng thoả mãn tính chất "đồng dạng Touchard": Nếu p là số nguyên tố bất kỳ thì

B_{p+n}\equiv B_{n}+B_{n+1}\ (\operatorname {mod} \ p).

Mỗi số Bell là tổng của các "số Stirling hạng hai"

B_{n}=\sum _{k=1}^{n}S(n,k).

Số Stirling S(n, k) là số các phân hoạch tập hợp n phần tử thành đúng k tập con không rỗng.

Số Bell thứ n cũng là tổng các hệ số trong đa thức có biểu thức của momen thứ n của phân phối xác suất bất kỳ như một hàm của n tích luỹ đầu tiên.

Chuỗi hàm luỹ thừa của các số Bell là

\sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}x^{n}=e^{e^{x}-1}.

Công thức tiệm cận

Công thức tiệm cận của các số Bell là

B_{n}\sim {\frac {1}{\sqrt {n}}}\left[{\lambda \left(n\right)}\right]^{n+{\frac {1}{2}}}e^{\lambda \left(n\right)-n-1}.

Trong đó $\lambda (n)=e^{W(n)},$ , W là hàm Lambert W.

(Lovász, 1993)

Lược đồ tam giác của các số Bell

Các số Bell có thể dễ dàng tính bằng cách xây dựng tam giác Bell, còn được gọi là dãy Aitken hoặc tam giác Peirce:

Bắt đầu với số một. Đặt số này trên dòng thứ nhất.
Tạo một dòng mới bằng việc lấy phầh tử cực phải của dòng ngay trên nó làm phần tử đầu tiên bên trái của dòng mới
Lần lượt tính các số tiếp theo của dòng mới bằng cách lấy tổng phần tử bên trái nó với phần tử đứng cùng cột phàn tử ấy ở dòng trước nó
Tiếp tục bước ba cho đến khi số phần tử của dòng mới nhiều hơn số phần tử của dòng trên một phần tử
Số nằm phía trái mỗi dòng là số Bell cho mỗi dòng.

Như vây, dòng thứ nhất chỉ gồm số 1. Dòng tiếp theo (thứ hai) được tạo ra bằng cách lấy phần tử đầu tiên bên phải của dòng trên đặt vào vị trí đầu tiên bên trái. Ta có:

 1
 1 x

Giá trị của x là tổng của hai phần tử ở cột tước nó cúng dòng (là 1) và dòng trên (cũng là 1) bằng 2.

 1
 1 2
 y

Giá trị y bằng giá trị đầu tiên tính từ bên phải của dòng trên (bằng 2), và tiếp theo:

 1
 1 2
 2 3 x

Bằng cách ấy ta có 5 dòng đầu của tam giác là:

 1
 1 2
 2 3 5
 5 7 10 15
15 20 27 37 52

Dòng thứ năm được tính như sau:

Lấy 15 từ dòng thứ tư
15 + 5 = 20
20 + 7 = 27
27 + 10 = 37
37 + 15 = 52

Số đứng ở dòng thứ n và côth thứ k là số các phân hoạch của tập {1,..., n} sao cho n là không cùng một lớp với bất kỳ số nào trong các phần tử k, k + 1,..., n − 1. Chẳng hạn có 7 phân hoặc của {1,..., 4} sao cho 4 không cùng lớp với các phần tử 2, 3, và có 10 phân hoạch của {1,..., 4} sao cho 4 không cùng lớp với phần tử 3. Hiệu của hai số trên (bằng 3) là số các phân hoạch của {1,..., 4} sao cho 4 cùng lớp với 2 nhưng không cùng lớp với 3. Số này có ngiã rằng có 3 phân hoặc của {1,..., 3} sao cho 3 không cùng lớp với 2.

Dùng phương pháp này có thể tính nhờ JavaScript như trên cho 219 số Bell đầu tiên:

function write_bell (hBound) { // writes Bell-0,..., Bell-hBound
var value = [ 123.456, 1 ] // value [0] = unimportant, value [1] = 1
for (var rowNr = 0; rowNr <= hBound; rowNr ++) {
value [rowNr] = value [1]
for (var colNr = rowNr - 1; colNr >= 1; colNr--) value [colNr] += value [colNr+1]
document.write ('Bell-' + rowNr + ' = ' + value [1] + '<br>')
}
}
write_bell (218)

Các số nguyên tố Bell

Một số nguyên tố Bell là một số Bell đồng thời là số nguyên tố. Các số nguyên tố Bell đầu tiên là:

2, 5, 877, 27644437, 35742549198872617291353508656626642567, 359334085968622831041960188598043661065388726959079837

tương ứng với các số Bell thứ 2, 3, 7, 13, 42 và 55. Số nguyên tố Bell tiếp theo là B₂₈₄₁, xấp xỉ với 9.3074 × 10⁶⁵³⁸.

Tới năm 2005, số nguyên tố Bell lớn nhất đã biết là B₂₈₄₁. Phil Carmody phát biểu rằng nó là số nguyên tố năm 2002. Gần hai năm sau, Ignacio Larrosa Canestro đã chứng minh rằng nó là số nguyên tố.

Xem thêm

Liên kết

Diagrams of Bell numbers.
Using the Bell Triangle to calculate Bell numbers. Lưu trữ 2010-05-01 tại Wayback Machine

Chú thích

^ Gardner 1978.

Tham khảo

[FOOTNOTEGardner1978-1] Gardner 1978.

[1]