Tranh chỉ đinh

Đường cong Bézier bậc hai trong Tranh chỉ đinh: Các điểm cuối (•) và điểm kiểm soát (×) xác định Đường cong Bézier bậc hai (⋯). Cung là một đoạn của parabol.

Tranh chỉ đinh hoặc nghệ thuật đinh và chỉ được tạo nên bởi một sợi chỉ duy nhất quấn quanh hệ thống đinh được đóng chặt trên Mặt phẳng. Các đường thẳng được tạo ra khi sợi chỉ quanh 2 đinh. Nhiều đường thẳng khi giao nhau và thay đổi nhiều góc độ tạo ra sự xuất hiện của các Đường cong Bézier bậc hai. Từ những Đường cong Bézier bậc hai sẽ tiếp tục tạo ra hình ảnh như việc vẽ tranh bằng bút chì^[1].

Tranh chỉ đinh do Mary Everest Boole phát minh vào cuối thế kỷ 19 để làm cho các ý tưởng toán học dễ tiếp cận hơn với trẻ em.^[2]Nó đã được phổ biến như một nghề Thủ công mỹ nghệ vào cuối những năm 1960 thông qua các bộ dụng cụ và sách hướng dẫn cách làm.^[3]

Năm 2016, Petros Vrellis áp dụng thuật toán số hóa cho ra một chuỗi các chữ số bằng Máy tính để tạo ra tác phẩm nghệ thuật Tranh chỉ đinh. Người dùng chỉ cần quấn chỉ từ cây đinh tương ứng với con số này đến cây đinh ứng với số khác bằng một sợi chỉ duy nhất^[4].

Hình ảnh

• 
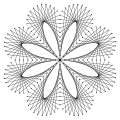
  Tranh chỉ đinh hình ngôi sao
• 
  Tranh chỉ đinh chân dung Petros Vrellis (2016)
• 
  Mô hình lỗ hoa
• 
  Mẫu may đầy hoa
• 
  Mẫu móc vòng hoa
• 
  Mẫu may nửa vòng hoa
• 
  Tranh chỉ đinh thể hiện hình chiếu của đa giác 8 chiều 4₂₁ polytope

Xem thêm

• Đường cong Bézier
• Toán học và nghệ thuật

Tham khảo

1. "Chàng trai vẽ chân dung bằng đinh và chỉ".
2. Michalowicz, Karen Dee Ann (1996). "Mary Everest Boole: An Erstwhile Pedagogist for Contemporary Times". Trong Calinger, Ronald (biên tập). Vita mathematica. Cambridge: Cambridge University Press. tr. 291. ISBN 0-88385-097-4.
3. Blanken, Rain, author. (ngày 15 tháng 6 năm 2018). String art magic : the secrets to crafting geometric art with string and nail. ISBN 978-1-940611-73-0. OCLC 988301633. {{Chú thích sách}}: |last= có tên chung (trợ giúp)
4. Bown, Oliver (2021). "Beyond the Creative Species: Making Machines That Make Art and Music". The MIT Press. ISBN 9780262045018.

Sách hướng dẫn

• Lois Kreischer (1971). Symmography. Crown Publishers, New York, NY. ISBN 0-517-50274-7
• Robert Sharpton (1972). Designing In String. Cunningham Art Products, Inc. No ISBN.
• Mark Jansen, Ric Barline, Fred Fortune (1972). The Art of Geometric Thread Design. Open Door Company, Campbell, CA. No ISBN.
• Brian and Patricia Eales (1973). Pin and Thread. Flarepath Printers Ltd., Great Britain. No ISBN.
• Glen D. Saeger (1973). String Things You Can Make. Sterling Publishing Co., New York, NY. ISBN 0-8069-5262-8
• Glen D. Saeger (1973). String Designs. Sterling Publishing Co., New York, NY. ISBN 0-8069-5320-9
• Vivian Bowler (1974). 44 String and Nail Art Projects. Crown Publishers, New York, NY. No ISBN.
• James E. Gick (1974). Thread Design. Hazel Pearson Crafts, Rosemead, CA. No ISBN.
• Douglas K. Dix (1975). Filography. Pan Books Ltd., London. ISBN 0-330-24155-9
• Robert Sharpton (1975). String Art: Step-By-Step. Chilton Book Co. Radnor, PA. ISBN 0-8019-6131-9
• Marie-Claude Riviere (1975). Pin Pictures With Wire and Thread. Sterling Publishing Co., New York, NY. ISBN ?
• Fran Risting (1975). String Art. Drake Publishing, NY and London. ISBN 0-87749-816-4
• Unknown Author (1975). String Art Made Easy. Clapper Publications Co. Ridge Park, Illinois. No ISBN.
• Compilation (1976). String Art Encyclopedia. Sterling Publishing Co., New York, NY. ISBN 0-8069-5362-4
• Richard Ohanian (1976). The Family Creative Workshop. Plenary Publications International, New York, NY. ISBN 0-88459-017-8
• Warren Farnworth (1977). Techniques and Designs in Pin and Thread Craft. BT Batsford Ltd., London. ISBN 0-7134-0535-X
• Roland and Dominique Cauro (1978). Stringcraft. Sterling Publishing Co., New York, NY. ISBN 0-8069-5364-0
• Raymond Gautard (1978). The Beautiful String Art Book. Sterling Publishing Co., New York, NY. ISBN 0-8069-5386-1
• Jon Millington (1989). 'Curve Stitching'. Tarquin Publications, London, UK ISBN 0-9062-1265-0
• Jane Hermsen (2003). Spirelli. Forte Publishers BV, The Netherlands. ISBN 90-5877-271-3
• Ali Gökçe Yılmaz (2013). "Futursuz Futurist String Art". Istanbul. No ISBN
• Rain Blanken (2018) "String Art Magic: Secrets to Crafting Geometric Art with String and Nail" ISBN 978-1-940611-73-0

Liên kết ngoài

• String art FAQs
• Basic string art how-to guide