Thuật toán

Lưu đồ thuật toán (thuật toán Euclid) để tính ước số chung lớn nhất (ưcln) của hai số a và b ở các vị trí có tên A và B. Thuật toán tiến hành bằng các phép trừ liên tiếp trong hai vòng lặp: NẾU phép thử B ≥ A cho kết quả "đúng" (chính xác hơn, số b ở vị trí B lớn hơn hoặc bằng số a ở vị trí A) thì thuật toán chỉ định B ← B - A (nghĩa là số b - a thay thế b cũ). Tương tự, IF A> B, THEN A ← A - B. Quá trình kết thúc khi (nội dung của) B bằng 0, tạo ra ưcln trong A. (Thuật toán bắt nguồn từ Scott 2009: 13; các ký hiệu và kiểu vẽ từ Tausworthe 1977).

Trong toán học và khoa học máy tính, một thuật toán, còn gọi là giải thuật, là một tập hợp hữu hạn các hướng dẫn được xác định rõ ràng, có thể thực hiện được bằng máy tính, thường để giải quyết một lớp vấn đề hoặc để thực hiện một phép tính.^[1][2] Các thuật toán luôn rõ ràng và được sử dụng chỉ rõ việc thực hiện các phép tính, xử lý dữ liệu, suy luận tự động và các tác vụ khác.

Là một phương pháp hiệu quả, một thuật toán có thể được biểu diễn trong một khoảng không gian và thời gian hữu hạn,^[3] và bằng một ngôn ngữ hình thức được xác định rõ ràng ^[4] để tính toán một hàm số.^[5] Bắt đầu từ trạng thái ban đầu và đầu vào ban đầu (có thể trống),^[6] các hướng dẫn mô tả một phép tính, khi được thực thi, sẽ tiến hành qua một số ^[7] hữu hạn các trạng thái kế tiếp được xác định rõ, cuối cùng tạo ra "đầu ra" ^[8] và chấm dứt ở trạng thái kết thúc cuối cùng. Sự chuyển đổi từ trạng thái này sang trạng thái tiếp theo không nhất thiết phải mang tính xác định; một số thuật toán, được gọi là thuật toán ngẫu nhiên, kết hợp đầu vào ngẫu nhiên.^[9]

Khái niệm thuật toán đã tồn tại từ thời cổ đại. Các thuật toán số học, chẳng hạn như thuật toán chia, được sử dụng bởi các nhà toán học Babylon cổ đại vào khoảng 2500 TCN và các nhà toán học Ai Cập vào khoảng 1550 TCN.^[10] Các nhà toán học Hy Lạp sau đó đã sử dụng các thuật toán trong sàng Eratosthenes để tìm số nguyên tố,^[11] và thuật toán Euclide để tìm ước chung lớn nhất của hai số.^[12] Các nhà toán học Ả Rập như al-Kindi vào thế kỷ thứ 9 đã sử dụng các thuật toán mật mã để phá mã, dựa trên phân tích tần số.^[13]

Bản thân từ thuật toán (algorithm) từ bắt nguồn từ nhà toán học thế kỷ thứ 9 Muḥammad ibn Mūsā al-Khwārizmī, tên ông được Latinh hóa thành Algoritmi.^[14] Việc chính thức hóa một phần những gì sẽ trở thành khái niệm thuật toán hiện đại bắt đầu với nỗ lực giải Entscheidungsproblem (vấn đề quyết định) do David Hilbert đặt ra vào năm 1928. Các công thức hóa sau này được đóng khung như những nỗ lực để xác định " khả năng tính toán hiệu quả " ^[15] hoặc "phương pháp hiệu quả".^[16] Những công thức hóa đó bao gồm các hàm đệ quy Gödel - Herbrand - Kleene của các năm 1930, 1934 và 1935, phép tính lambda của Alonzo Church năm 1936, Công thức 1 của Emil Post năm 1936 và các máy Turing của Alan Turing năm 1936–37 và 1939.

Định nghĩa không chính thức

Một định nghĩa không chính thức có thể là "một tập hợp các quy tắc xác định chính xác một chuỗi hoạt động",^[17] mà sẽ bao gồm tất cả các chương trình máy tính (bao gồm cả các chương trình không thực hiện phép tính số) và (ví dụ) bất kỳ thủ tục hành chính quy định nào ^[18] hoặc công thức nấu ăn.^[19]

Nói chung, một chương trình chỉ là một thuật toán nếu cuối cùng nó dừng lại ^[20] - mặc dù các vòng lặp vô hạn đôi khi có thể chấp nhận được.

Một ví dụ nguyên mẫu của một thuật toán là thuật toán Euclid, được sử dụng để xác định ước chung lớn nhất của hai số nguyên; một ví dụ được mô tả bằng lưu đồ ở trên và là ví dụ trong phần sau.

Boolos, Jeffrey & 1974, 1999Lỗi harv: không có mục tiêu: CITEREFBoolosJeffrey1999 (trợ giúp) đưa ra một định nghĩa không chính thức cho thuật toán như sau:

• Không một con người nào có thể viết đủ nhanh, đủ dài, hoặc đủ nhỏ † († "nhỏ hơn và nhỏ hơn mà không có giới hạn... bạn đang cố viết trên phân tử, trên nguyên tử, trên electron") để liệt kê tất cả các thành viên của vô số thiết lập bằng cách viết ra tên của họ, cái khác, trong một số ký hiệu. Nhưng con người có thể làm điều gì đó hữu ích không kém, trong trường hợp có nhiều tập hợp vô hạn nhất định: Họ có thể đưa ra các chỉ dẫn rõ ràng để xác định phần tử thứ n của tập hợp, cho n hữu hạn tùy ý. Những hướng dẫn như vậy phải được đưa ra khá rõ ràng, dưới hình thức mà chúng có thể được tuân theo bởi một máy tính toán hoặc bởi một con người chỉ có khả năng thực hiện các thao tác rất cơ bản trên các ký hiệu. ^[21]

"Tập hợp vô hạn liệt kê được" là tập hợp mà các phần tử của nó có thể được song ánh tương ứng 1-1 với các số nguyên. Vì vậy, Boolos và Jeffrey đang nói rằng một thuật toán ngụ ý hướng dẫn cho một quá trình "tạo" các số nguyên đầu ra từ một số nguyên "đầu vào" tùy ý hoặc các số nguyên, theo lý thuyết, có thể lớn tùy ý. Ví dụ: một thuật toán có thể là một phương trình đại số chẳng hạn như y = m + n (tức là hai "biến đầu vào" tùy ý m và n tạo ra đầu ra y), nhưng các nỗ lực của các tác giả khác nhau để xác định khái niệm cho thấy rằng từ đó ngụ ý nhiều hơn thế này, một cái gì đó theo thứ tự của (cho ví dụ bổ sung):

• Các hướng dẫn chính xác (bằng ngôn ngữ mà "máy tính" hiểu được) ^[22] để có một quy trình "tốt" ^[23] nhanh, hiệu quả, chỉ định các "động thái" của "máy tính" (máy hoặc con người, được trang bị bên trong thông tin và khả năng) ^[24] để tìm, giải mã và sau đó xử lý các số nguyên / ký hiệu đầu vào tùy ý m và n, ký hiệu + và = … và "hiệu quả" ^[25]

sản xuất ra, trong một thời gian "hợp lý",^[26] đầu ra-số nguyên y tại một nơi được chỉ định và với định dạng được chỉ định.

Khái niệm thuật toán cũng được sử dụng để định nghĩa khái niệm về khả năng giải mã — một khái niệm trung tâm để giải thích cách các hệ thống hình thức ra đời bắt đầu từ một tập hợp nhỏ các tiên đề và quy tắc. Về mặt logic, thời gian mà một thuật toán yêu cầu để hoàn thành không thể đo được, vì nó dường như không liên quan đến kích thước vật lý thông thường. Từ sự không chắc chắn như vậy, đặc trưng cho công việc đang diễn ra, dẫn đến việc không có định nghĩa thuật toán phù hợp với cả cách sử dụng thuật ngữ này một cách cụ thể (theo một nghĩa nào đó)

Hình thức hóa

Các thuật toán rất cần thiết cho cách máy tính xử lý dữ liệu. Nhiều chương trình máy tính chứa các thuật toán trình bày chi tiết các hướng dẫn cụ thể mà máy tính phải thực hiện — theo một thứ tự cụ thể — để thực hiện một nhiệm vụ cụ thể, chẳng hạn như tính tiền lương của nhân viên hoặc in phiếu điểm của học sinh. Vì vậy, một thuật toán có thể được coi là bất kỳ chuỗi hoạt động nào có thể được mô phỏng bởi một hệ thống hoàn chỉnh Turing. Các tác giả khẳng định luận điểm này bao gồm Minsky (1967), Savage (1987) và Gurevich (2000):

• Minsky: "Nhưng chúng tôi cũng sẽ duy trì, với Turing... rằng bất kỳ thủ tục nào có thể" tự nhiên "được gọi là hiệu quả, trên thực tế, có thể được thực hiện bởi một chiếc máy (đơn giản). Mặc dù điều này có vẻ cực đoan, nhưng những lập luận… ủng hộ nó thì khó có thể bác bỏ ”.^[27]
• Gurevich: “… Lập luận không chính thức của Turing ủng hộ luận điểm của ông ấy biện minh cho luận điểm mạnh mẽ hơn: mọi thuật toán đều có thể được mô phỏng bởi máy Turing… theo Savage [1987], thuật toán là một quá trình tính toán được xác định bởi máy Turing".^[28]

Máy Turing có thể xác định các quy trình tính toán không kết thúc. Các định nghĩa không chính thức của thuật toán thường yêu cầu thuật toán luôn kết thúc. Yêu cầu này làm cho nhiệm vụ quyết định xem một thủ tục chính thức có phải là một thuật toán không trong trường hợp chung - do một định lý chính của lý thuyết tính toán được gọi là bài toán dừng.

Thông thường, khi một thuật toán được liên kết với xử lý thông tin, dữ liệu có thể được đọc từ nguồn đầu vào, được ghi vào thiết bị đầu ra và được lưu trữ để xử lý thêm. Dữ liệu được lưu trữ được coi là một phần của trạng thái bên trong của thực thể thực hiện thuật toán. Trong thực tế, trạng thái được lưu trữ trong một hoặc nhiều cấu trúc dữ liệu.

Đối với một số quá trình tính toán này, thuật toán phải được xác định chặt chẽ: được chỉ định theo cách nó áp dụng trong mọi trường hợp có thể phát sinh. Điều này có nghĩa là mọi bước có điều kiện phải được xử lý một cách có hệ thống, theo từng trường hợp cụ thể; các tiêu chí cho từng trường hợp phải rõ ràng (và có thể tính toán được).

Bởi vì một thuật toán là một danh sách chính xác của các bước chính xác, thứ tự tính toán luôn quan trọng đối với hoạt động của thuật toán. Các hướng dẫn thường được giả định là được liệt kê rõ ràng và được mô tả là bắt đầu "từ trên cùng" và đi "xuống dưới cùng" —một ý tưởng được mô tả chính thức hơn bằng luồng kiểm soát.

Cho đến nay, cuộc thảo luận về việc chính thức hóa một thuật toán đã giả định các tiền đề của lập trình mệnh lệnh. Đây là quan niệm phổ biến nhất - một quan niệm cố gắng mô tả một nhiệm vụ bằng các phương tiện "máy móc", rời rạc. Duy nhất cho quan niệm về các thuật toán chính thức hóa này là phép toán gán, đặt giá trị của một biến. Nó bắt nguồn từ trực giác của " bộ nhớ " như một bàn di chuột. Dưới đây là một ví dụ về sự phân công như vậy.

Đối với một số quan niệm thay thế về những gì tạo thành một thuật toán, hãy xem lập trình hàm và lập trình logic.

Diễn đạt thuật toán

Các thuật toán có thể được thể hiện bằng nhiều loại ký hiệu, bao gồm ngôn ngữ tự nhiên, mã giả, lưu đồ, biểu đồ drakon, ngôn ngữ lập trình hoặc bảng điều khiển (được xử lý bởi trình thông dịch). Các biểu thức ngôn ngữ tự nhiên của các thuật toán có xu hướng dài dòng và mơ hồ, và hiếm khi được sử dụng cho các thuật toán phức tạp hoặc kỹ thuật. Mã giả, lưu đồ, biểu đồ drakon và bảng điều khiển là những cách có cấu trúc để thể hiện các thuật toán tránh nhiều sự mơ hồ thường gặp trong các câu lệnh dựa trên ngôn ngữ tự nhiên. Các ngôn ngữ lập trình chủ yếu nhằm mục đích thể hiện các thuật toán dưới dạng có thể được thực thi bởi máy tính, nhưng cũng thường được sử dụng như một cách để định nghĩa hoặc tài liệu hóa các thuật toán.

Có thể có nhiều cách biểu diễn khác nhau và người ta có thể thể hiện một chương trình máy Turing nhất định dưới dạng một chuỗi các bảng máy (xem máy trạng thái hữu hạn, bảng chuyển đổi trạng thái và bảng điều khiển để biết thêm), dưới dạng lưu đồ và biểu đồ drakon (xem biểu đồ trạng thái để biết thêm), hoặc như một dạng mã máy thô sơ hoặc mã lắp ráp được gọi là "bộ tứ" (xem máy Turing để biết thêm).

Các đại diện của thuật toán có thể được phân loại thành ba cấp độ được chấp nhận của mô tả máy Turing, như sau:^[29]

1. Mô tả cấp cao

“… Văn xuôi để mô tả một thuật toán, bỏ qua các chi tiết triển khai. Ở cấp độ này, chúng tôi không cần phải đề cập đến cách máy quản lý băng hoặc đầu từ của nó."

2. Mô tả triển khai

“… Văn xuôi được sử dụng để xác định cách máy Turing sử dụng đầu vào của nó và cách nó lưu trữ dữ liệu trên băng của nó. Ở cấp độ này, chúng tôi không đưa ra thông tin chi tiết về các trạng thái hoặc chức năng chuyển tiếp. "

3. Mô tả chính thức

Chi tiết nhất, "mức thấp nhất", đưa ra "bảng trạng thái" của máy Turing.

Thiết kế

Thiết kế thuật toán đề cập đến một phương pháp hoặc một quy trình toán học để giải quyết vấn đề và các thuật toán kỹ thuật. Việc thiết kế các thuật toán là một phần của nhiều lý thuyết giải pháp nghiên cứu hoạt động, chẳng hạn như lập trình động và chia để trị. Các kỹ thuật thiết kế và triển khai các thiết kế thuật toán còn được gọi là các mẫu thiết kế thuật toán,^[30] với các ví dụ bao gồm mẫu phương pháp mẫu và mẫu trang trí.

Một trong những khía cạnh quan trọng nhất của thiết kế thuật toán nằm ở việc tạo ra thuật toán có thời gian chạy hiệu quả, còn được gọi là Big O của nó.

Các bước điển hình trong quá trình phát triển thuật toán:

1. Định nghĩa vấn đề
2. Phát triển một mô hình
3. Đặc điểm kỹ thuật của thuật toán
4. Thiết kế một thuật toán
5. Kiểm tra tính đúng đắn của thuật toán
6. Phân tích thuật toán
7. Thực hiện thuật toán
8. Chương trình thử nghiệm
9. Viết tài liệu

Thực hiện

Thuật toán NAND logic được triển khai điện tử trong chip 7400

Enaliarctos

Hầu hết các thuật toán được thiết kế để thực hiện như các chương trình máy tính. Tuy nhiên, các thuật toán cũng được thực hiện bằng các phương tiện khác, chẳng hạn như trong mạng nơ-ron sinh học (ví dụ, não người thực hiện phép tính số học hoặc côn trùng đang tìm kiếm thức ăn), trong mạch điện hoặc trong một thiết bị cơ khí.

Thuật toán máy tính

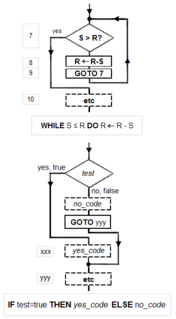
Các ví dụ về lưu đồ về cấu trúc Böhm-Jacopini chính tắc: SEQUENCE (hình chữ nhật xuống trang), WHILE-DO và IF-THEN-ELSE. Ba cấu trúc được tạo bởi GOTO có điều kiện nguyên thủy ({{{1}}}) (hình thoi), GOTO không điều kiện (hình chữ nhật), các toán tử gán khác nhau (hình chữ nhật) và HALT (hình chữ nhật). Việc lồng các cấu trúc này vào bên trong các khối gán dẫn đến các sơ đồ phức tạp (xem Tausworthe 1977: 100, 114).

Trong các hệ thống máy tính, thuật toán về cơ bản là một ví dụ của logic được viết trong phần mềm bởi các nhà phát triển phần mềm, để có hiệu quả đối với (các) máy tính "đích" nhằm tạo ra đầu ra từ đầu vào (có thể là rỗng) nhất định. Một thuật toán tối ưu, thậm chí chạy trong phần cứng cũ, sẽ tạo ra kết quả nhanh hơn thuật toán không tối ưu (độ phức tạp thời gian cao hơn) cho cùng mục đích, chạy trong phần cứng hiệu quả hơn; đó là lý do tại sao các thuật toán, như phần cứng máy tính, được coi là công nghệ.

Chương trình "thanh lịch" (nhỏ gọn), chương trình "tốt" (nhanh): Khái niệm "đơn giản và thanh lịch" xuất hiện không chính thức ở Knuth và chính xác là ở Chaitin:

• Knuth: "… chúng tôi muốn có các thuật toán tốt theo một khía cạnh thẩm mỹ được xác định lỏng lẻo. Một tiêu chí… là khoảng thời gian thực hiện thuật toán…. Các tiêu chí khác là khả năng thích ứng của thuật toán với máy tính, tính đơn giản và sang trọng của nó, v.v. " ^[31]
• Chaitin: "… một chương trình là 'thanh lịch', theo ý tôi thì đó là chương trình nhỏ nhất có thể để tạo ra kết quả đầu ra mà nó thực hiện" ^[32]

Chaitin mở đầu cho định nghĩa của mình bằng: "Tôi sẽ cho bạn thấy rằng bạn không thể chứng minh rằng một chương trình là 'thanh lịch '" —chẳng hạn như một bằng chứng sẽ giải quyết được bài toán tạm dừng (ibid).

Thuật toán so với hàm có thể tính toán bằng một thuật toán: Đối với một hàm đã cho, nhiều thuật toán có thể tồn tại. Điều này đúng, ngay cả khi không mở rộng tập lệnh có sẵn cho lập trình viên. Rogers nhận xét rằng “Điều quan trọng là phải phân biệt giữa khái niệm thuật toán, tức là thủ tục và khái niệm hàm có thể tính toán bằng thuật toán, tức là ánh xạ được tạo ra bởi thủ tục. Cùng một chức năng có thể có một số thuật toán khác nhau ".^[33]

Thật không may, có thể có sự cân bằng giữa tính tốt (tốc độ) và tính thanh lịch (tính nhỏ gọn) —một chương trình thanh lịch có thể cần nhiều bước để hoàn thành một phép tính hơn một chương trình kém thanh lịch hơn. Ví dụ sử dụng thuật toán Euclid xuất hiện bên dưới.

Máy tính, các mô hình tính toán: Máy tính (hay "máy tính" của con người ^[34]) là một loại máy bị hạn chế, một "thiết bị cơ khí xác định rời rạc" ^[35] làm theo hướng dẫn của nó một cách mù quáng.^[36] Các mô hình sơ khai của Melzak và Lambek ^[37] giảm khái niệm này thành bốn yếu tố: (i) các vị trí rời rạc, dễ phân biệt, (ii) các bộ đếm rời rạc, không thể phân biệt được ^[38] (iii) một tác nhân, và (iv) một danh sách các hướng dẫn có hiệu quả so với khả năng của tác nhân.^[39]

Minsky mô tả một biến thể phù hợp hơn của mô hình "bàn tính" của Lambek trong "Các cơ sở rất đơn giản để tính toán " của ông.^[40] Máy của Minsky tiến hành tuần tự thông qua năm (hoặc sáu, tùy thuộc vào cách đếm) lệnh, trừ khi IF – THEN GOTO có điều kiện hoặc GOTO không điều kiện thay đổi luồng chương trình không theo trình tự. Bên cạnh HALT, máy của Minsky bao gồm ba hoạt động gán (thay thế, thay thế) ^[41]: ZERO (ví dụ: nội dung của vị trí được thay thế bằng 0: L ← 0), SUCCESSOR (ví dụ: L ← L + 1) và DECREMENT (ví dụ: L ← L - 1).^[42] Hiếm khi một lập trình viên phải viết "mã" với một tập lệnh giới hạn như vậy. Nhưng Minsky cho thấy (Melzak và Lambek cũng vậy) rằng cỗ máy của anh ấy là Turing hoàn chỉnh với chỉ bốn loại lệnh chung: GOTO có điều kiện, GOTO vô điều kiện, gán / thay thế / thay thế và HALT. Tuy nhiên, một số hướng dẫn gán khác nhau (ví dụ: DECREMENT, INCREMENT và ZERO / CLEAR / EMPTY cho máy Minsky) cũng được yêu cầu đối với tính năng Turing-completeness; đặc điểm kỹ thuật chính xác của chúng phần nào tùy thuộc vào nhà thiết kế. GOTO vô điều kiện là một sự tiện lợi; nó có thể được xây dựng bằng cách khởi tạo một vị trí chuyên dụng bằng 0, ví dụ như lệnh "Z ← 0"; sau đó lệnh IF Z = 0 THEN GOTO xxx là vô điều kiện.

Mô phỏng thuật toán: ngôn ngữ máy tính (computor): Knuth khuyên người đọc rằng "cách tốt nhất để học một thuật toán là thử nó.. Lấy ngay giấy bút và làm việc với một ví dụ".^[43] Nhưng những gì về một mô phỏng hoặc thực hiện các điều thực tế? Lập trình viên phải dịch thuật toán sang ngôn ngữ mà trình mô phỏng / máy tính / trình biên dịch có thể thực thi một cách hiệu quả. Stone đưa ra một ví dụ về điều này: khi tính toán căn bậc hai, người tính toán phải biết cách lấy căn bậc hai. Nếu không, thì thuật toán, để có hiệu quả, phải cung cấp một bộ quy tắc để trích xuất căn bậc hai.^[44]

Điều này có nghĩa là lập trình viên phải biết một "ngôn ngữ" có hiệu quả so với tác nhân tính toán mục tiêu (máy tính). Nhưng mô hình nào nên được sử dụng cho mô phỏng? Van Emde Boas nhận xét "ngay cả khi chúng ta đặt lý thuyết phức tạp dựa trên lý thuyết trừu tượng thay vì máy móc cụ thể, sự tùy tiện trong việc lựa chọn mô hình vẫn còn. Chính tại thời điểm này, khái niệm mô phỏng đi vào ".^[45] Khi tốc độ đang được đo, tập lệnh quan trọng. Ví dụ, chương trình con trong thuật toán Euclid để tính phần còn lại sẽ thực thi nhanh hơn nhiều nếu lập trình viên có sẵn lệnh " modulus " thay vì chỉ phép trừ (hoặc tệ hơn: chỉ "giảm dần" của Minsky).

Lập trình có cấu trúc, cấu trúc chuẩn: Theo luận điểm của Church – Turing, bất kỳ thuật toán nào cũng có thể được tính toán bằng một mô hình được gọi là Turing hoàn chỉnh và theo các minh chứng của Minsky, tính đầy đủ của Turing chỉ yêu cầu bốn loại lệnh — GOTO có điều kiện, GOTO không điều kiện, phép gán, HALT. Kemeny và Kurtz nhận thấy rằng, trong khi việc sử dụng "vô kỷ luật" GOTO vô điều kiện và IF-THEN GOTO có điều kiện có thể dẫn đến " mã spaghetti ", một lập trình viên có thể viết các chương trình có cấu trúc chỉ bằng các hướng dẫn này; mặt khác "cũng có thể, và không quá khó, để viết các chương trình có cấu trúc tồi bằng một ngôn ngữ có cấu trúc".^[46] Tausworthe tăng cường ba cấu trúc kinh điển Böhm-Jacopini:^[47] SEQUENCE, IF-THEN-ELSE và WHILE-DO, với hai cấu trúc khác: DO-WHILE và CASE.^[48] Một lợi ích bổ sung của chương trình có cấu trúc là nó tự cho mình các bằng chứng về tính đúng đắn bằng cách sử dụng quy nạp toán học.^[49]

Các ký hiệu lưu đồ hợp quy: Phụ tá đồ họa được gọi là lưu đồ, đưa ra cách mô tả và ghi lại một thuật toán (và một chương trình máy tính của một thuật toán). Giống như quy trình chương trình của máy Minsky, lưu đồ luôn bắt đầu ở đầu trang và tiếp tục xuống. Các ký hiệu chính của nó chỉ có bốn: mũi tên có hướng hiển thị luồng chương trình, hình chữ nhật (SEQUENCE, GOTO), hình thoi (IF-THEN-ELSE) và dấu chấm (OR-tie). Các cấu trúc kinh điển Böhm – Jacopini được tạo ra từ những hình dạng nguyên thủy này. Cấu trúc con có thể "lồng" trong hình chữ nhật, nhưng chỉ khi một lối ra duy nhất xảy ra từ cấu trúc thượng tầng. Các ký hiệu và cách sử dụng chúng để xây dựng các cấu trúc chính tắc được thể hiện trong sơ đồ.

Ví dụ

Ví dụ thuật toán

Một trong những thuật toán đơn giản nhất là tìm số lớn nhất trong danh sách các số có thứ tự ngẫu nhiên. Tìm lời giải yêu cầu nhìn vào mọi số trong danh sách. Từ đó dẫn đến một thuật toán đơn giản, có thể được nêu trong phần mô tả cấp cao bằng văn xuôi tiếng Anh, như:

Mô tả cấp cao:

1. Nếu không có số nào trong tập hợp thì không có số cao nhất.
2. Giả sử số đầu tiên trong tập hợp là số lớn nhất trong tập hợp.
3. Với mỗi số còn lại trong tập hợp: nếu số này lớn hơn số lớn nhất hiện tại thì coi số này là số lớn nhất trong tập hợp.
4. Khi không còn số nào trong tập hợp để lặp lại, hãy coi số lớn nhất hiện tại là số lớn nhất của tập hợp.

Bán mô tả chính thức: Được viết bằng văn xuôi nhưng gần với ngôn ngữ cấp cao của chương trình máy tính hơn nhiều, sau đây là cách mã hóa chính thức hơn của thuật toán bằng mã giả hoặc mã pidgin:

Input: A list of numbers L. Output: The largest number in the list L.

 if L.size = 0 return null
 largest ← L[0]
 for each item in L, do
if item > largest, then
 largest ← item
 return largest

Thuật toán Euclid

Sơ đồ ví dụ về thuật toán Euclid từ TL Heath (1908), có thêm chi tiết. Euclid không vượt quá phép đo thứ ba và không đưa ra ví dụ số. Nic gastus đưa ra ví dụ về 49 và 21: "Tôi lấy số ít hơn trừ đi số lớn hơn; 28 là còn lại; sau đó một lần nữa tôi trừ cho điều này cùng 21 (vì điều này là có thể); còn lại là 7; tôi trừ đi 21, 14 được left; từ đó tôi lại trừ đi 7 (vì điều này là có thể); còn lại là 7, nhưng không thể trừ 7 từ 7. " Heath bình luận rằng "Cụm từ cuối cùng gây tò mò, nhưng ý nghĩa của nó là đủ rõ ràng, cũng như ý nghĩa của cụm từ về kết thúc 'tại một và cùng một số'." (Heath 1908: 300).

Thuật toán của Euclid để tính ước số chung lớn nhất (ƯCLN) cho hai số xuất hiện dưới dạng Mệnh đề II trong Quyển VII ("Lý thuyết số cơ bản") của tác phẩm Cơ sở của ông.^[50] Do đó, Euclid đặt ra vấn đề: "Cho hai số không nguyên tố với nhau, hãy tìm số đo chung lớn nhất của chúng". Ông định nghĩa "Một số [là] một vô số bao gồm các đơn vị": một số đếm, một số nguyên dương không bao gồm số không. Để "đo" là đặt một chiều dài ngắn s liên tiếp (q lần) lên trên chiều dài l cho đến khi phần còn lại là r nhỏ hơn chiều dài ngắn s. ^[51] Nói cách hiện đại, phần dư r = l - q × s, q là thương số, hoặc phần dư r là "môđun", phần nguyên còn lại sau phép chia.^[52]

Để phương pháp Euclid thành công, độ dài bắt đầu phải thỏa mãn hai yêu cầu: (i) độ dài không được bằng 0, VÀ (ii) phép trừ phải “hợp lệ”; tức là, một phép thử phải đảm bảo rằng số nhỏ hơn trong hai số bị trừ đi số lớn hơn (hoặc hai số có thể bằng nhau để phép trừ của chúng cho kết quả bằng không).

Chứng minh ban đầu của Euclid bổ sung thêm một yêu cầu thứ ba: hai độ dài không được nguyên tố với nhau. Euclid đã quy định điều này để ông có thể xây dựng một bằng chứng rút gọn là vô lý rằng số đo chung của hai số trên thực tế là lớn nhất.^[53] Trong khi thuật toán của Nicomachus cũng giống như thuật toán của Euclid, khi các số nguyên tố với nhau, nó mang lại số "1" cho số đo chung của chúng. Vì vậy, chính xác mà nói, sau đây thực sự là thuật toán của Nicomachus.

Biểu thức đồ họa của thuật toán Euclid để tìm ước số chung lớn nhất cho 1599 và 650.

 1599 = 650×2 + 299
 650 = 299×2 + 52
 299 = 52×5 + 39
 52 = 39×1 + 13
 39 = 13×3 + 0

Ngôn ngữ máy tính cho thuật toán Euclid

Chỉ một số loại lệnh được yêu cầu để thực thi thuật toán Euclid — một số phép thử logic (GOTO có điều kiện), GOTO không điều kiện, phép gán (thay thế) và phép trừ.

• Vị trí được ký hiệu bằng (các) chữ cái viết hoa, ví dụ: S, A, v.v.
• Số lượng (số) khác nhau ở một vị trí được viết bằng (các) chữ cái thường và (thường) được kết hợp với tên của vị trí. Ví dụ, vị trí L ở đầu có thể chứa số l = 3009.

Một chương trình đơn giản cho thuật toán Euclid

"Inelegant" là bản dịch của phiên bản thuật toán của Knuth với vòng lặp phần dư dựa trên phép trừ thay thế việc sử dụng phép chia (hoặc lệnh "modulus"). Bắt nguồn từ Knuth 1973: 2–4. Tùy thuộc vào hai số "Không phù hợp" có thể tính toán gcd trong ít bước hơn "Thanh lịch".

Thuật toán sau đây được đóng khung như là phiên bản bốn bước của Knuth của Euclid's và Nicomachus, nhưng thay vì sử dụng phép chia để tìm phần dư, nó sử dụng các phép trừ liên tiếp của độ dài s từ độ dài còn lại r cho đến khi r nhỏ hơn s. Mô tả cấp cao, được in đậm, được phỏng theo Knuth 1973: 2–4:

ĐẦU VÀO:

1 [Into two locations L and S put the numbers l and s that represent the two lengths]: INPUT L, S

2 [Initialize R: make the remaining length r equal to the starting/initial/input length l]: R ← L

E0: [Đảm bảo r ≥ s. ]

3 [Ensure the smaller of the two numbers is in S and the larger in R]: IF R > S THEN the contents of L is the larger number so skip over the exchange-steps 4, 5 and 6: GOTO step 6 ELSE swap the contents of R and S.

4 L ← R (this first step is redundant, but is useful for later discussion).

5 R ← S

6 S ← L

E1: [Tìm phần dư]: Cho đến khi độ dài còn lại r trong R nhỏ hơn độ dài ngắn hơn s trong S, lặp đi lặp lại phép trừ số đo s trong S với độ dài còn lại r trong R.

7 IF S > R THEN done measuring so GOTO 10 ELSE measure again,

8 R ← R − S

9 [Remainder-loop]: GOTO 7.

E2: [Phần dư có bằng 0? ]: HOẶC (i) số đo cuối cùng là chính xác, phần còn lại trong R bằng 0 và chương trình có thể tạm dừng, HOẶC (ii) thuật toán phải tiếp tục: số đo cuối cùng để lại phần dư trong R nhỏ hơn số đo trong S.

10 IF R = 0 THEN done so GOTO step 15 ELSE CONTINUE TO step 11,

E3: [Đảo vị trí s và r ]: Điểm mấu chốt của thuật toán Euclid. Sử dụng phần dư r để đo số trước đó nhỏ hơn s; L phục vụ như một kho lưu trữ tạm thời.

11 L ← R

12 R ← S

13 S ← L

14 [Repeat the measuring process]: GOTO 7

ĐẦU RA:

15 [Done. S contains the greatest common divisor]: PRINT S

XONG:

16 HALT, END, STOP.

Một chương trình đơn giản cho thuật toán Euclid

Phiên bản sau của thuật toán Euclid chỉ yêu cầu sáu lệnh cốt lõi để thực hiện mười ba lệnh được yêu cầu bởi "chương trình chưa thanh lịch"; tệ hơn nữa là "chương trình chưa thanh lịch" yêu cầu nhiều loại hướng dẫn hơn. [làm rõ] Bạn có thể tìm thấy sơ đồ của "Thanh lịch" ở đầu bài viết này. Trong ngôn ngữ BASIC (không có cấu trúc), các bước được đánh số, và lệnh LET [] = [] là lệnh gán được ký hiệu bằng ←.

 5 REM Euclid's algorithm for greatest common divisor
 6 PRINT "Type two integers greater than 0"
 10 INPUT A,B
 20 IF B=0 THEN GOTO 80
 30 IF A > B THEN GOTO 60
 40 LET B=B-A
 50 GOTO 20
 60 LET A=A-B
 70 GOTO 20
 80 PRINT A
 90 END

Cách "chương trình thanh lịch" hoạt động: Thay cho "vòng lặp Euclid" bên ngoài, "Elegant" di chuyển qua lại giữa hai "co-vòng lặp", một vòng lặp A> B tính A ← A - B và một vòng lặp B ≤ A tính toán B ← B - A. Điều này hoạt động bởi vì, khi cuối cùng giá trị nhỏ nhất M nhỏ hơn hoặc bằng dải con S (Chênh lệch = Minuend - Subtrahend), minuend có thể trở thành s (chiều dài đo mới) và subtrahend có thể trở thành r mới (độ dài được đo); nói cách khác, "ý nghĩa" của phép trừ đảo ngược. Phiên bản sau có thể được sử dụng với các ngôn ngữ hướng đối tượng:

// Euclid's algorithm for greatest common divisor
int euclidAlgorithm (int A, int B){
 A=Math.abs(A);
 B=Math.abs(B);
 while (B!=0){
   if (A>B) A=A-B;
   else B=B-A;
 }
 return A;
}

Kiểm tra các thuật toán Euclid

Một thuật toán có làm được những gì mà tác giả của nó muốn nó làm không? Một số trường hợp thử nghiệm thường cung cấp một số tin cậy về chức năng cốt lõi. Nhưng các thử nghiệm là không đủ. Đối với các trường hợp thử nghiệm, một nguồn ^[54] sử dụng 3009 và 884. Knuth đề xuất 40902, 24140. Một trường hợp thú vị khác là hai số nguyên tố cùng nhau 14157 và 5950.

Nhưng "trường hợp ngoại lệ" ^[55] phải được xác định và thử nghiệm. Liệu "Inelegant" có thực hiện đúng khi R> S, S> R, R = S không? Cũng vậy cho chương trình "Thanh lịch": B> A, A> B, A = B? (Có cho tất cả). Điều gì xảy ra khi một số bằng 0, cả hai số đều bằng không? ("Chưa thanh lịch" rơi vào vòng lặp vĩnh viễn trong các trường hợp trên; "Thanh lịch" rơi vào vòng lặp vĩnh viễn khi A = 0.) Điều gì xảy ra nếu người dùng nhập số âm ? Số phân số? Nếu các số đầu vào, tức là miền của hàm được tính toán bởi thuật toán / chương trình, chỉ bao gồm các số nguyên dương bao gồm cả số 0, thì các lỗi ở số 0 chỉ ra rằng thuật toán (và chương trình khởi tạo nó) là một hàm riêng phần chứ không phải một hàm tổng. Một thất bại đáng chú ý do các ngoại lệ kiểu như vậy là sự cố tên lửa Ariane 5 Flight 501 (ngày 4 tháng 6 năm 1996).

Chứng minh tính đúng đắn của chương trình bằng cách sử dụng quy nạp toán học: Knuth chứng minh việc áp dụng quy nạp toán học cho phiên bản "mở rộng" của thuật toán Euclid và ông đề xuất "một phương pháp chung áp dụng để chứng minh tính hợp lệ của bất kỳ thuật toán nào".^[56] Tausworthe đề xuất rằng thước đo độ phức tạp của một chương trình là độ dài của bằng chứng tính đúng đắn của nó.^[57]

Đo lường và cải thiện các thuật toán Euclid

Thanh lịch (nhỏ gọn) so với tốt (tốc độ): Chỉ với sáu lệnh cốt lõi, "Thanh lịch" là chiến thắng rõ ràng, so với "Không thanh lịch" với 13 lệnh. Tuy nhiên, "Không thanh lịch" nhanh hơn (nó đến HALT trong ít bước hơn). Phân tích thuật toán ^[58] chỉ ra lý do tại sao lại như vậy: "Thanh lịch" thực hiện hai phép thử điều kiện trong mỗi vòng trừ, trong khi "Không thanh lịch" chỉ thực hiện một phép thử. Vì thuật toán (thường) yêu cầu nhiều lần lặp lại, nên trung bình sẽ lãng phí nhiều thời gian để thực hiện "B = 0?" kiểm tra chỉ cần thiết sau khi phần còn lại được tính toán.

Các thuật toán có thể được cải thiện không?: Một khi lập trình viên đánh giá một chương trình "phù hợp" và "hiệu quả" - nghĩa là nó tính toán chức năng mà tác giả của nó dự định - thì câu hỏi sẽ trở thành, liệu nó có thể được cải thiện không?

Có thể cải thiện độ nhỏ gọn của "Không thanh lịch" bằng cách loại bỏ năm bước. Nhưng Chaitin đã chứng minh rằng việc nén một thuật toán không thể được tự động hóa bằng một thuật toán tổng quát;^[59] đúng hơn, nó chỉ có thể được thực hiện theo kinh nghiệm; tức là, bằng cách tìm kiếm đầy đủ, thử và sai, thông minh, sáng suốt, áp dụng suy luận quy nạp, v.v. Quan sát các bước 4, 5 và 6 được lặp lại trong các bước 11, 12 và 13. So sánh với "Thanh lịch" cung cấp gợi ý rằng các bước này, cùng với các bước 2 và 3, có thể bị loại bỏ. Điều này làm giảm số lượng lệnh cốt lõi từ 13 xuống 8, làm cho nó "thanh lịch" hơn "Thanh lịch", với chín bước.

Tốc độ của "Thanh lịch" có thể được cải thiện bằng cách di chuyển "B = 0?" kiểm tra bên ngoài của hai vòng trừ. Thay đổi này yêu cầu bổ sung ba lệnh (B = 0 ?, A = 0 ?, GOTO). Bây giờ "Thanh lịch" tính toán các số ví dụ nhanh hơn; cho dù điều này luôn đúng đối với bất kỳ A, B và R, S nào cho trước hay không sẽ yêu cầu một phân tích chi tiết.

Đọc thêm

• Độ phức tạp thuật toán
• Máy truy tìm dữ liệu
• Thuật toán sắp xếp

Tham khảo

1. “The Definitive Glossary of Higher Mathematical Jargon — Algorithm”. Math Vault (bằng tiếng Anh). ngày 1 tháng 8 năm 2019. Bản gốc lưu trữ ngày 28 tháng 2 năm 2020. Truy cập ngày 14 tháng 11 năm 2019.
2. “Definition oALGORITHM”. Merriam-Webster Online Dictionary (bằng tiếng Anh). Bản gốc lưu trữ ngày 14 tháng 2 năm 2020. Truy cập ngày 14 tháng 11 năm 2019.
3. "Any classical mathematical algorithm, for example, can be described in a finite number of English words" (Rogers 1987:2).
4. Well defined with respect to the agent that executes the algorithm: "There is a computing agent, usually human, which can react to the instructions and carry out the computations" (Rogers 1987:2).
5. "an algorithm is a procedure for computing a function (with respect to some chosen notation for integers)... this limitation (to numerical functions) results in no loss of generality", (Rogers 1987:1).
6. "An algorithm has zero or more inputs, i.e., quantities which are given to it initially before the algorithm begins" (Knuth 1973:5).
7. "A procedure which has all the characteristics of an algorithm except that it possibly lacks finiteness may be called a 'computational method'" (Knuth 1973:5).
8. "An algorithm has one or more outputs, i.e. quantities which have a specified relation to the inputs" (Knuth 1973:5).
9. Whether or not a process with random interior processes (not including the input) is an algorithm is debatable. Rogers opines that: "a computation is carried out in a discrete stepwise fashion, without the use of continuous methods or analogue devices... carried forward deterministically, without resort to random methods or devices, e.g., dice" (Rogers 1987:2).
10. Chabert, Jean-Luc (2012). A History of Algorithms: From the Pebble to the Microchip. Springer Science & Business Media. tr. 7–8. ISBN 9783642181924.
11. “Hellenistic Mathematics”. The Story of Mathematics. Bản gốc lưu trữ ngày 11 tháng 9 năm 2019. Truy cập ngày 14 tháng 11 năm 2019.
12. Cooke, Roger L. (2005). The History of Mathematics: A Brief Course. John Wiley & Sons. ISBN 978-1-118-46029-0.
13. Dooley, John F. (2013). A Brief History of Cryptology and Cryptographic Algorithms. Springer Science & Business Media. tr. 12–3. ISBN 9783319016283.
14. “Al-Khwarizmi - Islamic Mathematics”. The Story of Mathematics. Bản gốc lưu trữ ngày 25 tháng 7 năm 2019. Truy cập ngày 14 tháng 11 năm 2019.
15. Kleene 1943 in Davis 1965:274
16. Rosser 1939 in Davis 1965:225
17. Stone 1973:4
18. Simanowski, Roberto (2018). The Death Algorithm and Other Digital Dilemmas. Untimely Meditations. 14. Chase, Jefferson biên dịch. Cambridge, Massachusetts: MIT Press. tr. 147. ISBN 9780262536370. Bản gốc lưu trữ ngày 22 tháng 12 năm 2019. Truy cập ngày 27 tháng 5 năm 2019. [...] the next level of abstraction of central bureaucracy: globally operating algorithms.
19. Dietrich, Eric (2001) [1999]. “Algorithm”. Trong Wilson, Robert Andrew; Keil, Frank C. (biên tập). The MIT Encyclopedia of the Cognitive Sciences. MIT Cognet library. Cambridge, Massachusetts: MIT Press. tr. 11. ISBN 9780262731447. Truy cập ngày 22 tháng 7 năm 2020. An algorithm is a recipe, method, or technique for doing something.
20. Stone simply requires that "it must terminate in a finite number of steps" (Stone 1973:7–8).
21. Boolos and Jeffrey 1974,1999:19
22. cf Stone 1972:5
23. Knuth 1973:7 states: "In practice we not only want algorithms, we want good algorithms... one criterion of goodness is the length of time taken to perform the algorithm... other criteria are the adaptability of the algorithm to computers, its simplicity, and elegance, etc."
24. cf Stone 1973:6
25. Stone 1973:7–8 states that there must be, "...a procedure that a robot [i.e., computer] can follow in order to determine precisely how to obey the instruction". Stone adds finiteness of the process, and definiteness (having no ambiguity in the instructions) to this definition.
26. Knuth, loc. cit
27. Minsky 1967Lỗi harv: không có mục tiêu: CITEREFMinsky1967 (trợ giúp)
28. Gurevich 2000:1, 3
29. Sipser 2006:157
30. Algorithm Design: Foundations, Analysis, and Internet Examples, ISBN 978-0-471-38365-9
31. Knuth 1973:7
32. Chaitin 2005:32
33. Rogers 1987:1–2
34. In his essay "Calculations by Man and Machine: Conceptual Analysis" Seig 2002:390 credits this distinction to Robin Gandy, cf Wilfred Seig, et al., 2002 Reflections on the foundations of mathematics: Essays in honor of Solomon Feferman, Association for Symbolic Logic, A.K. Peters Ltd, Natick, MA.
35. cf Gandy 1980:126, Robin Gandy Church's Thesis and Principles for Mechanisms appearing on pp. 123–148 in J. Barwise et al. 1980 The Kleene Symposium, North-Holland Publishing Company.
36. A "robot": "A computer is a robot that performs any task that can be described as a sequence of instructions." cf Stone 1972:3
37. Lambek's "abacus" is a "countably infinite number of locations (holes, wires etc.) together with an unlimited supply of counters (pebbles, beads, etc). The locations are distinguishable, the counters are not". The holes have unlimited capacity, and standing by is an agent who understands and is able to carry out the list of instructions" (Lambek 1961:295). Lambek references Melzak who defines his Q-machine as "an indefinitely large number of locations... an indefinitely large supply of counters distributed among these locations, a program, and an operator whose sole purpose is to carry out the program" (Melzak 1961:283). B-B-J (loc. cit.) add the stipulation that the holes are "capable of holding any number of stones" (p. 46). Both Melzak and Lambek appear in The Canadian Mathematical Bulletin, vol. 4, no. 3, September 1961.
38. If no confusion results, the word "counters" can be dropped, and a location can be said to contain a single "number".
39. "We say that an instruction is effective if there is a procedure that the robot can follow in order to determine precisely how to obey the instruction." (Stone 1972:6)
40. cf Minsky 1967: Chapter 11 "Computer models" and Chapter 14 "Very Simple Bases for Computability" pp. 255–281 in particular
41. cf Knuth 1973:3.
42. But always preceded by IF–THEN to avoid improper subtraction.
43. Knuth 1973:4
44. Stone 1972:5. Methods for extracting roots are not trivial: see Methods of computing square roots.
45. Leeuwen, Jan (1990). Handbook of Theoretical Computer Science: Algorithms and complexity. Volume A. Elsevier. tr. 85. ISBN 978-0-444-88071-0.
46. John G. Kemeny và Thomas E. Kurtz 1985 Back to Basic: The History, Corruption, and Future of the Language, Addison-Wesley Publishing Company, Inc. Reading, MA, ISBN 0-201-13433-0.
47. Tausworthe 1977:101
48. Tausworthe 1977:142
49. Knuth 1973 section 1.2.1, expanded by Tausworthe 1977 at pages 100ff and Chapter 9.1
50. Heath 1908:300; Hawking's Dover 2005 edition derives from Heath.
51. " 'Let CD, measuring BF, leave FA less than itself.' This is a neat abbreviation for saying, measure along BA successive lengths equal to CD until a point F is reached such that the length FA remaining is less than CD; in other words, let BF be the largest exact multiple of CD contained in BA" (Heath 1908:297)
52. For modern treatments using division in the algorithm, see Hardy and Wright 1979:180, Knuth 1973:2 (Volume 1), plus more discussion of Euclid's algorithm in Knuth 1969:293–297 (Volume 2).
53. Euclid covers this question in his Proposition 1.
54. “Euclid's Elements, Book VII, Proposition 2”. Aleph0.clarku.edu. Bản gốc lưu trữ ngày 24 tháng 5 năm 2012. Truy cập ngày 20 tháng 5 năm 2012.
55. While this notion is in widespread use, it cannot be defined precisely.
56. Knuth 1973:13–18. He credits "the formulation of algorithm-proving in terms of assertions and induction" to R W. Floyd, Peter Naur, C.A.R. Hoare, H.H. Goldstine and J. von Neumann. Tausworth 1977 borrows Knuth's Euclid example and extends Knuth's method in section 9.1 Formal Proofs (pp. 288–298).zcsxucdsy
57. Tausworthe 1997:294
58. cf Knuth 1973:7 (Vol. I), and his more-detailed analyses on pp. 1969:294–313 (Vol II).
59. Breakdown occurs when an algorithm tries to compact itself. Success would solve the Huy Halting problem.