Danh sách số nguyên tố Mersenne và số hoàn hảo

Cách hình dung số 6 là số hoàn hảo

Đồ thị lôgarit của số chữ số của số nguyên tố lớn nhất đã biết theo năm phát hiện, gần như tất cả đều là số nguyên tố Mersenne

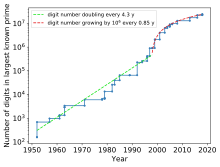
Số nguyên tố Mersenne và số hoàn hảo là hai loại số tự nhiên có quan hệ chặt chẽ với nhau trong lý thuyết số. Số nguyên tố Mersenne đặt theo tên nhà toán học Marin Mersenne là các số nguyên tố có thể biểu thị dưới dạng 2^p − 1 với p là số nguyên dương. Ví dụ, 3 là số nguyên tố Mersenne vì nó là số nguyên tố và có thể biểu diễn được dưới dạng 2² − 1.^[1][2] Bản thân các số p tương ứng với số nguyên tố Mersenne phải là số nguyên tố, nhưng ngược lại không phải mọi số nguyên tố p đều dẫn đến số nguyên tố Mersenne — ví dụ: 2¹¹ − 1 = 2047 = 23 × 89.^[3] Còn số hoàn hảo là số tự nhiên bằng tổng các ước số dương của chính nó, không bao gồm ước số là chính số đó. Theo đó, 6 là số hoàn hảo vì có các ước số (không bao gồm 6) là 1, 2, 3 và 1 + 2 + 3 = 6.^[2][4]

Tồn tại song ánh giữa các số nguyên tố Mersenne và số hoàn hảo chẵn được phát biểu trong Định lý Euclid–Euler, do Euclid chứng minh một phần và Leonhard Euler hoàn thiện: các số chẵn là hoàn hảo khi và chỉ khi biểu diễn được dưới dạng 2^{p − 1} × (2^p − 1), trong đó 2^p − 1 là số nguyên tố Mersenne. Nói cách khác, những số nào biểu diễn được dưới dạng đó thì là số hoàn hảo, và tất cả các số hoàn hảo chẵn đều có dạng đó. Ví dụ, khi p = 2, 2² − 1 = 3 là số nguyên tố và 2^{2 − 1} × (2² − 1) = 2 × 3 = 6 là số hoàn hảo.^[1][5][6]

Một bài toán mở hiện chưa có câu trả lời là số nguyên tố Mersenne và số hoàn hảo chẵn có phải tập vô hạn không.^[2][6] Tần suất phân bố số nguyên tố Mersenne được đề cập qua phỏng đoán Lenstra – Pomerance – Wagstaff phát biểu rằng số lượng số nguyên tố Mersenne nhỏ hơn x cho trước là (e^γ / log 2) × log log x, trong đó e là số Euler, γ là hằng số Euler còn log là logarit tự nhiên.^[7][8][9] Việc có tồn tại số hoàn hảo lẻ nào không hiện cũng chưa rõ; cũng như các điều kiện khác nhau về việc có thể tồn tại những số này, chẳng hạn như nếu có thì giới hạn dưới của chúng là 10¹⁵⁰⁰.^[10]

Danh sách dưới đây liệt kê tất cả các số nguyên tố Mersenne và số hoàn hảo hiện đã biết theo số mũ p tương ứng. Tính đến năm 2024^{[cập nhật]} đã khám phá được 52 số nguyên tố Mersenne (tương ứng với 52 số hoàn hảo), 18 số lớn nhất trong đó được phát hiện nhờ dự án máy tính phân tán Great Internet Mersenne Prime Search (Tìm kiếm số nguyên tố Mersenne khổng lồ trên Internet) viết tắt là GIMPS.^[2] Các số nguyên tố Mersenne mới được tìm thấy bằng Kiểm tra Lucas-Lehmer (Lucas-Lehmer test - LLT), một kiểm tra tính nguyên tố dành cho số nguyên tố Mersenne theo cách hiệu quả đối với máy tính nhị phân.^[2]

Các chỉ số xếp theo thứ tự tăng dần. Tính đến năm 2022^{[cập nhật]} vẫn có một xác suất nhỏ rằng thứ hạng có thể thay đổi nếu phát hiện được số nhỏ hơn. Theo GIMPS, tất cả các khả năng nhỏ hơn số mũ thích hợp thứ 48 là p = 57.885.161 đều đã được kiểm tra và xác minh đến tháng 1 năm 2024.^[11] Năm và người phát hiện được tính theo thời điểm cho số nguyên tố Mersenne, vì số hoàn hảo được tính theo hệ quả định lý Euclid-Euler. "GIMPS / tên" được dùng để chỉ những số nguyên tố được phát hiện bởi GIMPS và cá nhân đã phát hiện ra số nguyên tố đó. Các số về sau quá dài không viết hết được trong khuôn khổ nên chỉ hiển thị 6 chữ số đầu và 6 chữ số cuối.

Danh sách

Bảng 52 số nguyên tố Mersenne đã biết hiện tại và số hoàn hảo tương ứng

STT	p	Số nguyên tố Mersenne	Độ dài chữ số số nguyên tố Mersenne	Số hoàn hảo	Độ dài chữ số của số hoàn hảo	Thời điểm phát hiện	Người phát hiện	Phương pháp	Tham khảo
1	2	3	1	6	1	Thời cổ đại[a]	Ghi nhận cho các nhà toán học Hy Lạp cổ đại	Không ghi lại	[12][13][14]
2	3	7	1	28	2				[12][13][14]
3	5	31	2	496	3				[12][13][14]
4	7	127	3	8128	4				[12][13][14]
5	13	8191	4	33550336	8	khoảng 1456[b]	Khuyết danh[c]	Chia thử	[13][14]
6	17	131071	6	8589869056	10	1588[b]	Pietro Cataldi		[2][17]
7	19	524287	6	137438691328	12				[2][18]
8	31	2147483647	10	230584...952128	19	1772	Leonhard Euler	Chia thử bằng giới hạn module	[19][20]
9	61	230584...693951	19	265845...842176	37	tháng 11 năm 1883	Ivan M. Pervushin	Dãy Lucas	[21]
10	89	618970...562111	27	191561...169216	54	tháng 6 năm 1911	Ralph Ernest Powers		[22]
11	107	162259...288127	33	131640...728128	65	1 tháng 6 năm 1914			[23]
12	127	170141...105727	39	144740...152128	77	10 tháng 1 năm 1876	Édouard Lucas		[24]
13	521	686479...057151	157	235627...646976	314	30 tháng 1 năm 1952	Raphael M. Robinson	LLT trên SWAC[d]	[25]
14	607	531137...728127	183	141053...328128	366				[25]
15	1.279	104079...729087	386	541625...291328	770	25 tháng 6 năm 1952			[26]
16	2.203	147597...771007	664	108925...782528	1.327	7 tháng 10 năm 1952			[27]
17	2.281	446087...836351	687	994970...915776	1.373	9 tháng 10 năm 1952			[27]
18	3.217	259117...315071	969	335708...525056	1.937	8 tháng 9 năm 1957	Hans Riesel	LLT trên BESK[e]	[28]
19	4.253	190797...484991	1.281	182017...377536	2,561	3 tháng 11 năm 1961	Alexander Hurwitz	LLT trên IBM 7090[f]	[29]
20	4.423	285542...580607	1.332	407672...534528	2.663				[29]
21	9.689	478220...754111	2.917	114347...577216	5.834	11 tháng 5 năm 1963	Donald B. Gillies	LLT trên ILLIAC II[g]	[30]
22	9.941	346088...463551	2.993	598885...496576	5.985	16 tháng 5 năm 1963			[30]
23	11.213	281411...392191	3.376	395961...086336	6.751	2 tháng 6 năm 1963			[30]
24	19.937	431542...041471	6.002	931144...942656	12.003	4 tháng 3 năm 1971	Bryant Tuckerman	LLT trên IBM 360/91	[31]
25	21.701	448679...882751	6.533	100656...605376	13.066	30 tháng 10 năm 1978	Landon Curt Noll & Laura Nickel	LLT trên CDC Cyber[h] 174	[32]
26	23.209	402874...264511	6.987	811537...666816	13.973	9 tháng 2 năm 1979	Landon Curt Noll		[32]
27	44.497	854509...228671	13.395	365093...827456	26.790	8 tháng 4 năm 1979	Harry L. Nelson & David Slowinski	LLT trên Cray-1[i]	[33][34]
28	86.243	536927...438207	25.962	144145...406528	51.924	25 tháng 9 năm 1982	David Slowinski		[35]
29	110.503	521928...515007	33,265	136204...862528	66.530	29 tháng 1 năm 1988	Walter Colquitt & Luke Welsh	LLT trên NEC SX-2[j]	[36][37]
30	132.049	512740...061311	39.751	131451...550016	79.502	19 tháng 9 năm 1983	David Slowinski và cộng sự (Cray)	LLT trên Cray X-MP	[38]
31	216.091	746093...528447	65.050	278327...880128	130.100	1 tháng 9 năm 1985		LLT trên Cray X-MP/24	[39][40]
32	756.839	174135...677887	227.832	151616...731328	455.663	17 tháng 2 năm 1992		LLT trên Cray-2 của Harwell Lab	[41]
33	859.433	129498...142591	258.716	838488...167936	517.430	4 tháng 1 năm 1994		LLT trên Cray C90	[42]
34	1.257.787	412245...366527	378.632	849732...704128	757.263	3 tháng 9 năm 1996		LLT trên Cray T94	[43][44]
35	1.398.269	814717...315711	420.921	331882...375616	841.842	13 tháng 11 năm 1996	GIMPS / Joel Armengaud	LLT / Prime95 trên PC Pentium 90 MHz	[45]
36	2.976.221	623340...201151	895.932	194276...462976	1.791.864	24 tháng 8 năm 1997	GIMPS / Gordon Spence	LLT / Prime95 trên PC Pentium 100 MHz	[46]
37	3.021.377	127411...694271	909.526	811686...457856	1.819.050	27 tháng 1 năm 1998	GIMPS / Roland Clarkson	LLT / Prime95 trên PC Pentium 200 MHz	[47]
38	6.972.593	437075...193791	2.098.960	955176...572736	4.197.919	1 tháng 6 năm 1999	GIMPS / Nayan Hajratwala	LLT / Prime95 trên IBM Aptiva[k] với bộ vi xử lý Pentium II 350 MHz	[48]
39	13.466.917	924947...259071	4.053.946	427764...021056	8.107.892	14 tháng 11 năm 2001	GIMPS / Michael Cameron	LLT / Prime95 trên PC với bộ vi xử lý Athlon T-Bird 800 MHz	[49]
40	20.996.011	125976...682047	6.320.430	793508...896128	12.640.858	17 tháng 11 năm 2003	GIMPS / Michael Shafer	LLT / Prime95 trên PC Dell Dimension với bộ vi xử lý Pentium 4 2 GHz	[50]
41	24.036.583	299410...969407	7.235.733	448233...950528	14.471.465	15 tháng 5 năm 2004	GIMPS / Josh Findley	LLT / Prime95 trên PC với bộ vi xử lý Pentium 4 2.4 GHz	[51]
42	25.964.951	122164...077247	7.816.230	746209...088128	15.632.458	18 tháng 2 năm 2005	GIMPS / Martin Nowak		[52]
43	30.402.457	315416...943871	9.152.052	497437...704256	18.304.103	15 tháng 12 năm 2005	GIMPS / Curtis Cooper & Steven Boone	LLT / Prime95 trên PC tại Đại học Trung Missouri (UCM)	[53]
44	32.582.657	124575...967871	9.808.358	775946...120256	19.616.714	4 tháng 9 năm 2006			[54]
45	37.156.667	202254...220927	11.185.272	204534...480128	22.370.543	tháng 9 năm 2008	GIMPS / Hans-Michael Elvenich	LLT / Prime95 trên PC	[55]
46	42.643.801	169873...314751	12.837.064	144285...253376	25.674.127	4 tháng 6 năm 2009[l]	GIMPS / Odd Magnar Strindmo	LLT / Prime95 trên PC với bộ vi xử lý Intel Core 2 3 GHz	[56]
47	43.112.609	316470...152511	12.978.189	500767...378816	25.956.377	23 tháng 8 năm 2008	GIMPS / Edson Smith	LLT / Prime95 trên PC Dell OptiPlex với bộ vi xử lý Intel Core 2 Duo E6600	[55][57][58]
48	57.885.161	581887...285951	17.425.170	169296...130176	34.850.340	25 tháng 1 năm 2013	GIMPS / Curtis Cooper	LLT / Prime95 trên PC tại Đại học Trung Missouri	[59][60]
?	69.369.389	Mức nhỏ nhất chưa được xác minh[m]
49?[n]	74.207.281	300376...436351	22.338.618	451129...315776	44.677.235	7 tháng 1 năm 2016[o]	GIMPS / Curtis Cooper	LLT / Prime95 trên PC với bộ vi xử lý Intel Core i7-4790	[61][62][63]
50?[n]	77.232.917	467333...179071	23.249.425	109200...301056	46.498.850	26 tháng 12 năm 2017	GIMPS / Jonathan Pace	LLT / Prime95 trên PC với bộ vi xử lý Intel Core i5-6600	[64][65][66]
51?[n]	82.589.933	148894...902591	24.862.048	110847...207936	49.724.095	7 tháng 12 năm 2018	GIMPS / Patrick Laroche	LLT / Prime95 trên PC với bộ vi xử lý Intel Core i5-4590T	[67][68]
?	124.399.361	Mức nhỏ nhất chưa được kiểm tra[m]
52?[n]	136.279.841	881694...871551	41.024.320	388692...008576	82.048.640	12 tháng 10 năm 2024	GIMPS / Luke Durant	LLT / GpuOwl trên bộ vi xử lý NVIDIA H100 GPU	[69]

Ghi chú

1. Bốn số hoàn hảo đầu tiên được Nicomachus nghiên cứu khoảng năm 100, và khái niệm này (tương ứng với số nguyên tố Mersenne) được Euclid biết đến và chép trong bộ Cơ sở. Không có ghi nhận về việc phát hiện.
2. ^ Các nhà Toán học Hồi giáo Trung Cổ như Ismail ibn Ibrahim ibn Fallus (1194–1239) có thể biết về số hoàn hảo thứ năm đến thứ bảy trước khi châu Âu ghi nhận.^[15]
3. Tìm thấy trong bản thảo khuyết danh Codex latinus monacensis 14908 ra đời khoảng từ năm 1456 đến 1461^[13][16]
4. Standards Western Automatic Computer - Máy tính điện tử của NIST năm 1950
5. Binär Elektronisk SekvensKalkylator - Máy tính điện tử đầu tiên của Thụy Điển 1953–1966
6. Máy tính lớn tốc độ 100 Kflop/s bắt đầu hoạt động từ tháng 12 năm 1959
7. Siêu máy tính của Đại học Illinois hoạt động từ năm 1962
8. Siêu máy tính của Control Data Corporation thập niên 1970, 1980
9. Siêu máy tính dùng bộ vi xử lý vector đầu tiên của hãng Cray Research ra mắt năm 1976.
10. Loạt siêu máy tính vector do NEC sản xuất, là những máy tính đầu tiên vượt 1 gigaflop và có tốc độ nhanh nhất thế giới vào những năm 1992–1993, 2002–2004
11. Máy tính cá nhân ra đời tháng 9 năm 1994
12. M_42.643.801 lần đầu thông báo tới GIMPS vào ngày 12 tháng 4 năm 2009 nhưng do lỗi máy chủ nên đến ngày 4 tháng 6 năm 2009 mới được con người ghi nhận.
13. ^ Tính đến ngày 24 tháng 10 năm 2024^{[cập nhật][11]}
14. ^ Chưa xác minh được liệu có tồn tại số nguyên tố Mersenne nào chưa được tìm ra giữa số thứ 48 (M_57.885.161) (đã chắc chắn) và thứ 51 (M_82.589.933) trên bảng này nên xếp hạng chỉ mang tính tạm thời.
15. M_74.207.281 lần đầu thông báo tới GIMPS vào ngày 17 tháng 9 năm 2015 nhưng do lỗi máy chủ nên đến ngày 7 tháng 1 năm 2016 mới được con người ghi nhận.

Chú thích

1. ^ Stillwell 2010, tr. 40.
2. ^ Caldwell, Chris K. “Mersenne Primes: History, Theorems and Lists” [Số nguyên tố Mersenne: Lịch sử, định lý và danh sách]. PrimePages (bằng tiếng Anh). Lưu trữ bản gốc ngày 4 tháng 10 năm 2021. Truy cập ngày 1 tháng 12 năm 2021.
3. Caldwell, Chris K. “If 2ⁿ-1 is prime, then so is n” [Nếu 2ⁿ-1 là số nguyên tố thì n là số nguyên tố]. PrimePages (bằng tiếng Anh). Lưu trữ bản gốc ngày 5 tháng 10 năm 2021. Truy cập ngày 1 tháng 12 năm 2021.
4. Prielipp 1970, tr. 692–696.
5. Caldwell, Chris K. “Characterizing all even perfect numbers” [Đặc trưng của tất cả các số hoàn hảo chẵn]. PrimePages (bằng tiếng Anh). Lưu trữ bản gốc ngày 8 tháng 10 năm 2014. Truy cập ngày 1 tháng 12 năm 2021.
6. ^ Crilly, Tony (2007). “Perfect numbers” [Số hoàn hảo]. 50 mathematical ideas you really need to know [50 ý tưởng toán học bạn thực sự cần biết] (bằng tiếng Anh). Quercus. ISBN 978-1-84724-008-8. Lưu trữ bản gốc ngày 13 tháng 10 năm 2021. Truy cập ngày 1 tháng 12 năm 2021.
7. Caldwell, Chris K. “Heuristics Model for the Distribution of Mersennes” [Mô hình Heuristic cho phân bố số nguyên tố Mersenne]. PrimePages (bằng tiếng Anh). Lưu trữ bản gốc ngày 5 tháng 10 năm 2021. Truy cập ngày 1 tháng 12 năm 2021.
8. Wagstaff 1983, tr. 385.
9. Pomerance 1981, tr. 97–105.
10. Ochem & Rao 2012, tr. 1869–1877.
11. ^ GIMPS, Milestones Report.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
12. ^ Heath 1908, tr. 421–425.
13. ^ Dickson 1919, tr. 4–6.
14. ^ Smith 1925, tr. 21.
15. O'Connor, John J.; Robertson, Edmund F. “Perfect numbers” [Số hoàn hảo]. MacTutor History of Mathematics archive (bằng tiếng Anh). Lưu trữ bản gốc ngày 5 tháng 10 năm 2021. Truy cập ngày 2 tháng 12 năm 2021.
16. “'Calendarium ecclesiasticum – BSB Clm 14908'”. Bavarian State Library. Lưu trữ bản gốc ngày 13 tháng 10 năm 2021. Truy cập ngày 2 tháng 12 năm 2021.
17. Cataldi 1603, tr. 12.
18. Cataldi 1603, tr. 20.
19. Caldwell, Chris K. “Modular restrictions on Mersenne divisors” [Giới hạn modul trên ước số Mersenne] (bằng tiếng Anh). PrimesPage. Bản gốc lưu trữ ngày 11 tháng 11 năm 2021. Truy cập ngày 2 tháng 12 năm 2021.
20. L'Académie Royale des Sciences et Belles-Lettres de Berlin 1774, tr. 35–36.
21. Bulletin de l'Académie impériale des sciences de St.-Pétersbourg 1887, tr. 532–533.
22. Powers 1911, tr. 195–197.
23. “Records of Proceedings at Meetings” [Hồ sơ kỷ yếu hội nghị]. Proceedings of the London Mathematical Society (bằng tiếng Anh). s2-13 (1): iv-xl. 1914. doi:10.1112/plms/s2-13.1.1-s.
24. Lucas 1876, tr. 165–167.
25. ^ AMS 1952a, tr. 58–61.
26. AMS 1952b, tr. 204.
27. ^ AMS 1953, tr. 67–72.
28. Riesel 1958, tr. 60.
29. ^ Hurwitz 1962, tr. 249.
30. ^ Gillies 1964, tr. 93–97.
31. Tuckerman 1971, tr. 2319–2320.
32. ^ Noll & Nickel 1980, tr. 1387–1390.
33. Slowinski 1978, tr. 258–261.
34. “Science Watch: A New Prime Number” [Thông tin khoa học: Một số nguyên tố mới]. The New York Times (bằng tiếng Anh). ngày 5 tháng 6 năm 1979. Truy cập ngày 13 tháng 10 năm 2021.
35. Ewing 1983, tr. 48.
36. Peterson 1988, tr. 85.
37. Colquitt & Welsh 1991, tr. 867–869.
38. “Number is largest prime found yet” [Số nguyên tố lớn nhất từng tìm thấy]. The Globe and Mail (bằng tiếng Anh). ngày 24 tháng 9 năm 1983 – qua ProQuest.
39. Peterson 1985, tr. 199.
40. Dembart, Lee (ngày 17 tháng 9 năm 1985). “Supercomputer Comes Up With Whopping Prime Number” [Siêu máy tính đưa ra số nguyên tố cực lớn]. Los Angeles Times (bằng tiếng Anh). Lưu trữ bản gốc ngày 2 tháng 11 năm 2021. Truy cập ngày 4 tháng 12 năm 2021.
41. Maddox 1992, tr. 283.
42. ComputerWorld 1994, tr. 73.
43. Caldwell, Chris K. “A Prime of Record Size! 2^1257787-1” [Kỷ lục độ lớn số nguyên tố! 2^1257787-1]. PrimePages (bằng tiếng Anh). Lưu trữ bản gốc ngày 5 tháng 10 năm 2021. Truy cập ngày 4 tháng 12 năm 2021.
44. Gillmor, Dan (ngày 3 tháng 9 năm 1996). “Crunching numbers: Researchers come up with prime math discovery” [Nghiền số: các nhà nghiên cứu trình bày khám phá số nguyên tố trong toán]. Knight Ridder (bằng tiếng Anh). Tribune Content Agency – qua Gale.
45. GIMPS, M1398269.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
46. GIMPS, M2976221.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
47. GIMPS, M3021377.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
48. GIMPS, M6972593.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
49. GIMPS, M13466917.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
50. GIMPS, M20996011.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
51. GIMPS, M24036583.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
52. GIMPS, M25964951.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
53. GIMPS, M30402457.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
54. GIMPS, M32582657.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
55. ^ GIMPS, M43112609.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
56. GIMPS, M42643801.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
57. Maugh, Thomas H. (ngày 27 tháng 9 năm 2008). “Rare prime number found” [Tìm thấy số nguyên tố hiếm]. Los Angeles Times (bằng tiếng Anh). Lưu trữ bản gốc ngày 27 tháng 7 năm 2021. Truy cập ngày 4 tháng 12 năm 2021.
58. Smith, Edson. “The UCLA Mersenne Prime” [Số nguyên tố Mersenne của UCLA]. UCLA Mathematics (bằng tiếng Anh). Lưu trữ bản gốc ngày 22 tháng 11 năm 2021. Truy cập ngày 4 tháng 12 năm 2021.
59. GIMPS, M57885161.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
60. Yirka, Bob (ngày 6 tháng 2 năm 2013). “University professor discovers largest prime number to date” [Giáo sư đại học khám phá số nguyên tố lớn nhất đến nay]. Phys.org (bằng tiếng Anh). Lưu trữ bản gốc ngày 16 tháng 1 năm 2021. Truy cập ngày 4 tháng 12 năm 2021.
61. GIMPS, M74207281.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
62. “Largest known prime number discovered in Missouri” [Số nguyên tố lớn nhất đến nay được tìm ra ở Missouri]. BBC News (bằng tiếng Anh). ngày 20 tháng 1 năm 2016. Lưu trữ bản gốc ngày 21 tháng 8 năm 2021. Truy cập ngày 4 tháng 12 năm 2021.
63. Thanh Tùng (ngày 26 tháng 1 năm 2016), “Tìm thấy số nguyên tố lớn nhất từ trước tới nay”, VnExpress, truy cập ngày 4 tháng 12 năm 2021
64. GIMPS, M77232917.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
65. Lamb, Evelyn (ngày 4 tháng 1 năm 2018). “Why You Should Care About a Prime Number That's 23,249,425 Digits Long” [Sao bạn nên quan tâm đến số nguyên tố có độ dài 23.249.425]. Slate Magazine (bằng tiếng Anh). Lưu trữ bản gốc ngày 9 tháng 10 năm 2021. Truy cập ngày 4 tháng 12 năm 2021.
66. Phương Hoa (ngày 7 tháng 1 năm 2018), “Tìm thấy số nguyên tố lớn nhất dài 9.000 trang”, VnExpress, truy cập ngày 4 tháng 12 năm 2021
67. GIMPS, M82589933.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)
68. Palca, Joe (ngày 21 tháng 12 năm 2018). “The World Has A New Largest-Known Prime Number” [Thế giới có số nguyên tố mới lớn nhất đã phát hiện]. NPR (bằng tiếng Anh). Lưu trữ bản gốc ngày 30 tháng 7 năm 2021. Truy cập ngày 4 tháng 12 năm 2021.
69. GIMPS, M136279841.Lỗi sfn: không có mục tiêu: CITEREFGIMPS (trợ giúp)

Thư mục

• L'Académie Royale des Sciences et Belles-Lettres de Berlin (1774), Nouveaux mémoires de L'Académie Royale des Sciences et Belles-Lettres avec L'Histoire pour la même année [Tân kỷ yếu thường niên của Viện Hàn lâm Khoa học Nghệ thuật và Lịch sử Hoàng gia] (bằng tiếng Pháp), 1772
• Bulletin de l'Académie impériale des sciences de St.-Pétersbourg (ngày 27 tháng 1 năm 1887), Sur un nouveau nombre premier, annoncé par le père Pervouchine [Về một số nguyên tố mới do Pervushin công bố] (bằng tiếng Pháp), XXXI
• Cataldi, Pietro Antonio (1603), Trattato de' numeri perfetti di Pietro Antonio Cataldo [Chuyên luận về số hoàn hảo của Pietro Antonio Cataldi về số hoàn hảo] (bằng tiếng La-tinh), Presso di Heredi di Giouanni Rossi
• Colquitt, W. N.; Welsh, L. (tháng 4 năm 1991). “A new Mersenne prime” [Số nguyên tố Mersenne mới]. Mathematics of Computation (bằng tiếng Anh). American Mathematical Society. 56 (194). Bibcode:1991MaCom..56..867C. doi:10.1090/S0025-5718-1991-1068823-9. JSTOR 2008415.
• Dickson, Leonard Eugene (1919), History of the Theory of Numbers [Lịch sử lý thuyết số] (bằng tiếng Anh), I, Washington: Carnegie Institution of Washington
• Ewing, John (tháng 3 năm 1983). “2⁸⁶²⁴³ - 1 is Prime” [2⁸⁶²⁴³ - 1 là số nguyên tố]. The Mathematical Intelligencer (bằng tiếng Anh). 5 (1). doi:10.1007/BF03023507. ISSN 0343-6993.
• Gillies, Donald B. (tháng 1 năm 1964). “Three new Mersenne primes and a statistical theory” [Ba số nguyên tố Mersenne mới và lý thuyết thống kê]. Mathematics of Computation (bằng tiếng Anh). American Mathematical Society. 18 (85). doi:10.1090/S0025-5718-1964-0159774-6. JSTOR 2003409.
• Hurwitz, Alexander (tháng 4 năm 1962). “New Mersenne primes” [Những cố nguyên tố Mersenne mới]. Mathematics of Computation (bằng tiếng Anh). American Mathematical Society. 16 (78). doi:10.1090/S0025-5718-1962-0146162-X. ISSN 0025-5718.
• Lucas, Édouard (1876), “Note sur l'application des séries récurrentes à la recherche de la loi de distribution des nombres premier” [Ghi chú về ứng dụng dãy số lặp vào tìm kiếm quy luật phân bố số nguyên tố], Comptes rendus de l'Académie des Sciences (bằng tiếng Pháp), 82
• Heath, T.L. biên tập (1908), The Thirteen Books of Euclid's Elements [Mười ba sách trong bộ Cơ sở của Euclid] (bằng tiếng Anh), Cambridge University Press
• Maddox, John (ngày 26 tháng 3 năm 1992). “The endless search for primality” [Cuộc tìm kiếm vô tận tính nguyên tố]. Nature (bằng tiếng Anh). 356 (6367). Bibcode:1992Natur.356..283M. doi:10.1038/356283a0. ISSN 1476-4687.
• Noll, Landon Curt; Nickel, Laura (tháng 10 năm 1980). “The 25th and 26th Mersenne primes” [Số nguyên tố Mersenne thứ 25 và 26]. Mathematics of Computation (bằng tiếng Anh). American Mathematical Society. 35 (152). doi:10.1090/S0025-5718-1980-0583517-4. JSTOR 2006405.
• Ochem, Pascal; Rao, Michaël (ngày 30 tháng 1 năm 2012), “Odd perfect numbers are greater than 10¹⁵⁰⁰” [Số hoàn hảo lẻ lớn hơn 10¹⁵⁰⁰], Mathematics of Computation (bằng tiếng Anh), American Mathematical Society, 81, doi:10.1090/S0025-5718-2012-02563-4, ISSN 0025-5718
• Peterson, I. (ngày 28 tháng 9 năm 1985). “Prime Time for Supercomputers” [Thời kỳ nguyên tố với siêu máy tính]. Science News (bằng tiếng Anh). 128 (13). doi:10.2307/3970245. JSTOR 3970245.
• —— (ngày 6 tháng 2 năm 1988). “Priming for a Lucky Strike” [Tìm ra số nguyên tố bằng cú may mắn]. Science News (bằng tiếng Anh). 133 (6). doi:10.2307/3972461. JSTOR 3972461.
• Pomerance, Carl (tháng 9 năm 1981), “Recent developments in primality testing” [Những phát triển gần đây về thử nghiệm tính nguyên tố], The Mathematical Intelligencer (bằng tiếng Anh), 3, doi:10.1007/BF03022861, ISSN 0343-6993
• Powers, Ralph Ernest (tháng 11 năm 1911). “The Tenth Perfect Number” [Số hoàn hảo thứ mười]. The American Mathematical Monthly (bằng tiếng Anh). 18 (11). doi:10.2307/2972574. JSTOR 2972574.
• Riesel, Hans (tháng 1 năm 1958). “A New Mersenne Prime” [Số nguyên tố Mersenne mới]. Mathematics of Computation (bằng tiếng Anh). American Mathematical Society. 12 (61). doi:10.1090/S0025-5718-58-99282-2.
• Prielipp, Robert W. (1970), “Perfect Numbers, Abundant Numbers, and Deficient Numbers” [Số hoàn hảo, số dư thừa và số khuyết], The Mathematics Teacher (bằng tiếng Anh), 63, doi:10.5951/MT.63.8.0692, JSTOR 27958492 – qua JSTOR
• Slowinski, David (1978). “Searching for the 27th Mersenne prime” [Tìm kiếm số nguyên tố Mersenne thứ 27]. Journal of Recreational Mathematics (bằng tiếng Anh). 11 (4).
• Smith, David Eugene (1925), History of Mathematics [Lịch sử toán học] (bằng tiếng Anh), II, Dover, ISBN 978-0-486-20430-7
• Stillwell, John (2010), Mathematics and Its History [Toán học và lịch sử toán học], Undergraduate Texts in Mathematics (bằng tiếng Anh), Springer Science+Business Media, ISBN 978-1-4419-6052-8
• Tuckerman, Bryant (tháng 10 năm 1971). “The 24th Mersenne Prime” [Số nguyên tố Mersenne thứ 24]. Proceedings of the National Academy of Sciences (bằng tiếng Anh). 68 (10). Bibcode:1971PNAS...68.2319T. doi:10.1073/pnas.68.10.2319. PMC 389411. PMID 16591945.
• Wagstaff, Samuel S. (tháng 1 năm 1983), “Divisors of Mersenne numbers” [Ước số Mersenne], Mathematics of Computation (bằng tiếng Anh), 40, doi:10.1090/S0025-5718-1983-0679454-X, ISSN 0025-5718
• “Notes” [Ghi chú]. Mathematics of Computation (bằng tiếng Anh). American Mathematical Society. 6 (37). tháng 1 năm 1952. doi:10.1090/S0025-5718-52-99405-2. ISSN 0025-5718.
• “Notes” [Ghi chú]. Mathematics of Computation (bằng tiếng Anh). American Mathematical Society. 6 (39). tháng 7 năm 1952. doi:10.1090/S0025-5718-52-99389-7. ISSN 0025-5718.
• “Notes” [Ghi chú]. Mathematics of Computation (bằng tiếng Anh). American Mathematical Society. 7 (41). tháng 1 năm 1953. doi:10.1090/S0025-5718-53-99372-7. ISSN 0025-5718.
• “Cray offers discount plan” [Cray mời chào kế hoạch giảm giá]. ComputerWorld (bằng tiếng Anh). 28 (3). ngày 17 tháng 1 năm 1994. ISSN 0010-4841.
• “Great Internet Mersenne Prime Search” [Tìm kiếm số nguyên tố Mersenne khổng lồ trên Internet] (bằng tiếng Anh). Lưu trữ bản gốc ngày 3 tháng 12 năm 2021. Truy cập ngày 4 tháng 12 năm 2021.

Liên kết ngoài

• Chuỗi OEIS A000043 (Số mũ tương ứng p) (tiếng Anh)
• Chuỗi OEIS A000396 (Số hoàn hảo) (tiếng Anh)
• Chuỗi OEIS A000668 (Số nguyên tố Mersenne) (tiếng Anh)

"Danh sách số nguyên tố Mersenne và số hoàn hảo" là một danh sách chọn lọc của Wikipedia tiếng Việt. Mời bạn xem phiên bản đã được bình chọn vào ngày 30 tháng 12 năm 2021 và so sánh sự khác biệt với phiên bản hiện tại.