Vật lý tính toán

Vật lý tính toán là việc nghiên cứu và thực hiện phân tích số để giải quyết các vấn đề trong vật lý học mà đã tồn tại một lý thuyết định lượng. Trong lịch sử, vật lý tính toán là ứng dụng đầu tiên của máy tính hiện đại trong khoa học, và bây giờ là một tập hợp con của khoa học tính toán.

Đôi khi vật lý tính toán được coi là một nhánh phụ (hoặc nhánh) của vật lý lý thuyết, nhưng những người khác coi nó là một nhánh trung gian giữa vật lý lý thuyết và vật lý thực nghiệm, một cách thứ ba bổ sung cho lý thuyết và thực nghiệm.

Tổng quan

Một đại diện cho bản chất đa ngành của vật lý tính toán vừa là sự chồng chéo của vật lý, toán học ứng dụng, vừa là khoa học máy tính và là cầu nối giữa chúng.

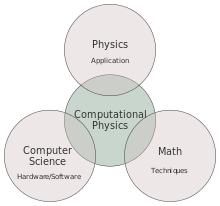
Trong vật lý, các lý thuyết khác nhau dựa trên các mô hình toán học cung cấp dự đoán rất chính xác về cách các hệ thống hoạt động. Thật không may, thường thì việc giải quyết mô hình toán học cho một hệ thống cụ thể để đưa ra một dự đoán hữu ích là không khả thi. Điều này có thể xảy ra, ví dụ, khi giải pháp không có biểu thức dạng đóng hoặc quá phức tạp. Trong những trường hợp như vậy, cần xấp xỉ bằng số. Vật lý tính toán là môn học liên quan đến các phép tính gần đúng số này: phép tính gần đúng của giải pháp được viết dưới dạng số hữu hạn (và thường là lớn) của các phép toán đơn giản (thuật toán) và máy tính được sử dụng để thực hiện các phép toán này và tính toán một giải gần đúng và lỗi tương ứng.

Vị trí của vật lý tính toán trong vật lý học

Có một cuộc tranh luận về tình trạng của tính toán trong phương pháp khoa học.

Đôi khi nó được coi là gần giống với vật lý lý thuyết; một số người khác coi mô phỏng máy tính là " thí nghiệm máy tính ", vẫn còn những người khác coi nó là một nhánh trung gian hoặc khác nhau giữa vật lý lý thuyết và vật lý thực nghiệm, cách thứ ba bổ sung cho lý thuyết và thí nghiệm. Mặc dù máy tính có thể được sử dụng trong các thí nghiệm để đo lường và ghi lại (và lưu trữ) dữ liệu, nhưng điều này rõ ràng không phải là một cách tiếp cận tính toán.

Những thách thức trong vật lý tính toán

Các vấn đề vật lý tính toán nói chung là rất khó để giải quyết chính xác. Điều này là do một số lý do (toán học): thiếu tính hòa tan đại số và/hoặc phân tích, độ phức tạp và hỗn loạn.

Ví dụ, - ngay cả những vấn đề đơn giản rõ ràng, chẳng hạn như tính toán hàm sóng của electron quay quanh nguyên tử trong điện trường mạnh (hiệu ứng Stark), có thể đòi hỏi nỗ lực rất lớn để xây dựng thuật toán thực tế (nếu có thể tìm thấy); các kỹ thuật cruder hoặc brute-force khác, như phương pháp đồ họa hoặc tìm kiếm gốc, có thể được yêu cầu. Về mặt nâng cao hơn, lý thuyết nhiễu loạn toán học đôi khi cũng được sử dụng (một tác phẩm được hiển thị cho ví dụ cụ thể này ở đây).

Ngoài ra, chi phí tính toán và độ phức tạp tính toán cho vấn đề đa cơ thể (và các đối tác cổ điển của chúng) có xu hướng tăng nhanh. Một hệ thống vĩ mô thường có kích thước cỡ ${\displaystyle 10^{23}}$ các hạt cấu thành, vì vậy nó là một phần của một vấn đề. Việc giải các bài toán cơ học lượng tử thường theo log hàm mũ theo kích thước của hệ ^[1] và đối với cơ thể N cổ điển, nó có độ phức tạp cấp N bình phương.

Cuối cùng, nhiều hệ thống vật lý vốn dĩ là phi tuyến tốt nhất và hỗn loạn tồi tệ nhất: điều này có nghĩa là khó có thể đảm bảo bất kỳ lỗi số nào không phát triển đến mức khiến cho 'giải pháp' trở nên vô dụng.

Tham khảo

1. Feynman, Richard P. (1982). “Simulating physics with computers”. International Journal of Theoretical Physics (bằng tiếng Anh). 21 (6–7): 467–488. doi:10.1007/bf02650179. ISSN 0020-7748. Article PDF