Phiêu bạt di truyền

Một phần của loạt bài viết về
Tiến hóa sinh học
Sẻ Darwin theo nét vẽ của John Gould
Chỉ mục Dẫn nhập Chính Đại cương Thuật ngữ Bằng chứng Lịch sử
Quá trình và kết quả Di truyền học quần thể Biến dị Đa dạng Đột biến Chọn lọc tự nhiên Thích nghi Đa hình Phiêu bạt di truyền Dòng gen Sự hình thành loài Phát xạ thích nghi Hợp tác Đồng tiến hóa Đồng tuyệt chủng Phân tách Hội tụ Song song Tuyệt chủng
Lịch sử tự nhiên Nguồn gốc sự sống Lịch sử tiến hóa Lịch trình tiến hóa Tiến hóa loài người Cây phát sinh Đa dạng sinh học Địa lý sinh học Phân loại Đơn vị phân loại tiến hóa Miêu tả theo nhánh học Hóa thạch chuyển tiếp Sự kiện tuyệt chủng
Lịch sử lý thuyết tiến hóa Tổng quan Phục Hưng Trước Darwin Darwin Nguồn gốc các loài Trước thuyết tổng hợp Thuyết tổng hợp hiện đại Tiến hóa phân tử Sinh học phát triển tiến hóa Nghiên cứu hiện tại Lịch sử phát sinh loài Lịch sử cổ sinh vật học (Dòng thời gian)
Lĩnh vực và ứng dụng Ứng dụng của tiến hóa Tội phạm học sinh học xã hội Di truyền học sinh thái Thẩm mĩ học tiến hóa Nhân loại học tiến hóa Mô hình hóa tiến hóa Kinh tế học tiến hóa Nhận thức luận tiến hóa Đạo đức học tiến hóa Lý thuyết trò chơi tiến hóa Ngôn ngữ học tiến hóa Y học tiến hóa Khoa học thần kinh tiến hóa Sinh lý học tiến hóa Tâm lý học tiến hóa Tiến hóa thực nghiệm Phát sinh chủng loại học Cổ sinh vật học Chọn giống vật nuôi Thí nghiệm về phát sinh loài Sinh học xã hội Hệ thống học Học thuyết Darwin tổng quát
Tác động xã hội Tiến hóa giữa vai trò sự thật và học thuyết Ảnh hưởng xã hội Mâu thuẫn giữa tiến hóa-tạo hóa Các cuộc chống đối thuyết tiến hóa Mức ủng hộ
Thể loại Chủ đề liên quan
x t s

Phiêu bạt di truyền, còn gọi là trôi dạt alen hoặc hiệu ứng Sewall Wright,^[1] là sự thay đổi tần số của một biến thể gen hiện tại (alen) trong quần thể do lấy mẫu ngẫu nhiên các sinh vật.^[2] Các alen ở con cái là một phần của bố mẹ và sự ngẫu nhiên quyết định một phần liệu một cá thể có thể sống sót và sinh sản hay không. Tần số alen của một quần thể là một phần của các bản sao của một gen có chung một dạng.^[3] Tần số alen của một quần thể là tỉ số số gen ở một dạng nhất định.^[4]

Trôi dạt gen có thể làm một số biến thể gen biến mất hoàn toàn và do đó làm giảm biến dị di truyền.^[5] Nó cũng có thể làm những alen hiếm xuất hiện thường xuyên hơn và thậm chí là cố định.

Khi có ít bản sao của một alen, tác động của trôi dạt gen là lớn hơn, và khi có nhiều bản sao của một alen thì tác động của trôi dạt gen trở nên nhỏ hơn. Giữa thế kỉ 20, nhiều cuộc tranh luận nổ ra xung quang tầm quan trọng của chọn lọc tự nhiên so với những quá trình trung tính, bao gồm trôi dạt gen. Ronald Fisher, người giải thích chọn lọc tự nhiên thông qua di truyền học Mendel,^[6] cho rằng trôi dạt gen chỉ đóng vai trò thứ yếu trong tiến hóa, và đây là quan điểm phổ biến trong vài thập kỉ. Năm 1968, nhà di truyền học quần thể Motoo Kimura khơi lại cuộc tranh luận với thuyết tiến hóa trung tính, cho rằng hầu hết trường hợp mà thay đổi trong gen truyền đi trong quần thể (tuy nhiên không nhất thiết là thay đổi trong kiểu hình) được gây ra bởi trôi dạt gen trên đột biến trung tính.^[3][7]

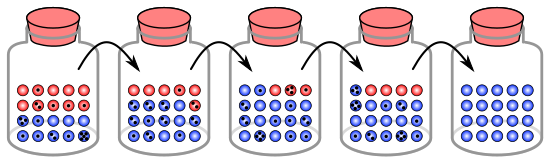
Ví dụ về bi trong lọ

Quá trình trôi dạt gen có thể được minh họa bằng một mô phỏng sử dụng 20 viên bi trong lọ, biểu diễn 20 cá thể trong một quần thể.^[8] Coi lọ này là quần thể ban đầu, trong đó có mười bi đỏ và mười bi xanh, biểu diễn hai loại alen của một gen có trong quần thể. Qua mỗi thế hệ, các cá thể trong quần thể sinh sản ngẫu nhiên. Để biểu diễn sự sinh sản này, chọn một viên bi trong lọ và thêm một viên bi cùng màu vào một lọ mới (viên bi được chọn vẫn nằm trong lọ cũ). Đây là "con" của viên bi gốc. Lặp lại quá trình này cho đến khi lọ mới có 20 viên bi, tức 20 "cá thể con". Trừ trường hợp lọ thứ hai có đúng 10 viên bi đỏ và 10 viên bi xanh thì tần số alen đã thay đổi ngẫu nhiên.

Nếu quá trình này được lặp lại nhiều lần, số bi đỏ và xanh được chọn mỗi lần sẽ thay đổi. Đôi khi một lọ sẽ có nhiều bi đỏ hơn lọ "bố mẹ" của nó và đôi khi ngược lại. Sự biến thiên trong số bi đỏ và bi xanh này tương tự như trôi dạt gen – một sự thay đổi trong tần số alen của quần thể do biến đổi ngẫu nhiên trong phân bố alen từ thế hệ này sang thế hệ tiếp theo.

Thậm chí còn có khả năng trong một thế hệ không có bi màu nào đó được chọn, tức chúng không có con cái. Trong ví dụ này, nếu không có bi đỏ nào được chọn, thế hệ tiếp theo sẽ chỉ chứa bi xanh. Nếu điều này xảy ra thì alen đỏ biến mất hoàn toàn khỏi quần thể, trong khi alen xanh trở nên cố định: tất cả thế hệ sau đó sẽ chỉ chứa alen xanh. Trong những quần thể nhỏ, cố định có thể xảy ra chỉ trong vài thế hệ.

Trong mô phỏng này, mỗi chấm đen trên bi cho biết nó đã được chọn để sao chép (sinh sản) một lần. Xuất hiện sự cố định "alen" xanh trong vòng năm thế hệ.

Xác suất và tần số alen

Cơ chế của trôi dạt gen có thể được minh họa bằng một ví dụ đơn giản. Xét một tập đoàn vi khuẩn rất lớn bị cô lập trong một giọt dung dịch. Các vi khuẩn có kiểu gen giống hệt nhau ngoại trừ một gen có hai alen là A và B. A và B là những alen trung tính, tức chúng không ảnh hưởng đến khả năng sinh tồn và sinh sản của vi khuẩn; tất cả các cá thể trong tập đoàn đều có khả năng sinh tồn và sinh sản như nhau. Giả sử ban đầu một nửa số vi khuẩn mang alen A và nửa còn lại mang alen B. Do đó A và B đều có tần số alen là 1/2.

Giọt dung dịch này sau đó thu nhỏ lại cho đến khi chỉ còn thức ăn để cung cấp cho bốn vi khuẩn. Tất cả những con vi khuẩn khác chết mà không sinh sản. Trong bốn con vi khuẩn còn lại này, có 16 tổ hợp khả dĩ cho các alen A và B:

(A-A-A-A), (B-A-A-A), (A-B-A-A), (B-B-A-A),
(A-A-B-A), (B-A-B-A), (A-B-B-A), (B-B-B-A),
(A-A-A-B), (B-A-A-B), (A-B-A-B), (B-B-A-B),
(A-A-B-B), (B-A-B-B), (A-B-B-B), (B-B-B-B).

Do tất cả các cá thể có xác suất sống sót bằng nhau, bốn cá thể này là một mẫu ngẫu nhiên lấy từ tập đoàn vi khuẩn ban đầu. Xác suất một trong bốn vi khuẩn này mang một alen nào đó là 1/2, do đó xác suất của một tổ hợp alen xuất hiện là

${\displaystyle {\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}={\frac {1}{16}}.}$

Nói cách khác, mỗi tổ hợp trong mười sáu tổ hợp alen trên có xác suất diễn ra là bằng nhau và đều bằng 1/16.

Đếm số tổ hợp theo số lượng alen A và B, ta được bảng sau.

Số alen A	Số alen B	Số tổ hợp	Xác suất
4	0	1	1/16
3	1	4	4/16
2	2	6	6/16
1	3	4	4/16
0	4	1	1/16

Số tổ hợp có số alen A bằng số alen B là sáu, và xác suất trường hợp này xảy ra là 6/16. Số tổ hợp còn lại là 10, do đó xác suất số alen A khác số alen B là 10/16. Như vậy, mặc dù tập đoàn ban đầu có số alen A bằng số alen B, có nhiều khả năng số alen trong quần thể với bốn cá thể không còn phân bố đều nữa. Trong trường hợp đó, đã xảy ra sự trôi dạt gen: tần số alen của quần thể đã thay đổi do lấy mẫu ngẫu nhiên. Trong ví dụ này quần thể thu nhỏ chỉ còn bốn cá thể, một hiện tượng gọi là cổ chai di truyền.

Xác suất có k bản sao của alen A (hoặc B) tồn tại (cột cuối cùng của bảng trên) có thể được tính sử dụng phân bố nhị thức với xác suất "thành công" (xác suất alen đó có mặt) là p là

${\displaystyle {n \choose k}p^{k}\left(1-p\right)^{n-k}.}$

Trong ví dụ trên, ta có n = 4 và p = 1/2.

Mô hình toán học

Mô hình toán học biểu diễn trôi dạt gen có thể được mô phỏng bằng quá trình rẽ nhánh hoặc phương trình khuếch tán mô tả thay đổi trong tần số alen của một quần thể lý tưởng.^[9]

Mô hình Wright–Fisher

Xét một gen với hai alen, A và B. Trong quần thể lưỡng bội có N cá thể thì có 2N bản sao của một gen. Một cá thể có thể có hai bản sao của một alen (đồng hợp) hoặc có cả hai alen (dị hợp). Ta có thể gọi tần số của một alen p và tần số của alen kia là q. Mô hình Wright–Fisher, đặt tên theo Sewall Wright và Ronald Fisher, giả sử rằng các thế hệ không chồng lặp (ví dụ, cây hàng năm có một thế hệ mỗi năm) và rằng mỗi bản sao của gen trong thế hệ mới được lấy ngẫu nhiên từ các bản sao của gen trong thế hệ trước đó. Công thức để tính xác suất có k bản sao của alen với xác suất p trong thế hệ vừa rồi là.^[10][11]

${\displaystyle {2N \choose k}p^{k}q^{2N-k}={\frac {(2N)!}{k!(2N-k)!}}p^{k}q^{2N-k}}$

trong đó ký hiệu "!" chỉ hàm giai thừa.

Mô hình Moran

Mô hình Moran cho phép các thế hệ chồng lặp. Ở mỗi bước, một cá thể được chọn để sinh sản (với cá thể con cùng loại alen với bố mẹ) và một cá thể được chọn để chết. Do đó tại mỗi thời điểm, số alen một loại nào đó có thể tăng một, giảm một, hoặc giữ nguyên. Do đó ma trận chuyển đổi của nó là tam chéo, tức các lời giải toán học cho mô hình Moran dễ dàng hơn so với mô hình Wright–Fisher. Mặt khác, mô phỏng máy tính thường được thực hiện với mô hình Wright–Fisher, do cần ít bước hơn. Trong mô hình Moran, cần N bước để trải qua một thế hệ, trong đó N là kích thước quần thể hiệu quả. Mô hình Wright–Fisher chỉ mất một bước để thực hiện một thế hệ.^[12]

Trong thực tế, mô hình Moran và mô hình Wright–Fisher cho kết quả tương tự nhau, nhưng trôi dạt gen thường xảy ra nhanh gấp đôi trong mô hình Moran.

Trôi dạt và cố định

Nguyên lý Hardy–Weinberg phát biểu rằng trong một quần thể ngẫu phối lớn, tần số alen không đổi từ thế hệ này sang thế hệ tiếp trừ khi cân bằng bị phá vỡ bởi di cư, đột biến gen, hoặc chọn lọc tự nhiên.^[13]

Tuy nhiên, trong quần thể hữu hạn, không alen mới nào được tạo thành từ việc lấy mẫu ngẫu nhiên của các alen cho thế hệ tiếp theo, nhưng việc lấy mẫu ngẫu nhiên có thể làm một alen hiện có biến mất. Do điều này có thể loại bỏ, nhưng không thể thay thế, một alen, và vì những sự tăng hoặc giảm ngẫu nhiên trong tần số alen tác động tới phân bố alen của thế hệ tiếp theo, trôi dạt di truyền có xu hướng khiến quần thể trở nên đồng nhất về mặt di truyền. Khi một alen có tần số là 1 (100%), nó được gọi là đã "cố định" trong quần thể, và khi một alen có tần số là 0 (0%) thì nó bị mất. Những quần thể nhỏ hơn đạt được sự cố định sớm hơn, còn trong một quần thể không giới hạn thì cố định không xảy ra. Khi một alen trở nên cố định, trôi dạt di truyền dừng lại, và tần số alen không thể thay đổi trừ khi một alen mới được đưa vào quần thể thông qua đột biến hoặc dòng gen. Như vậy, mặc dù trôi dạt di truyền là một quá trình ngẫu nhiên, không định hướng, nó vẫn có xu hướng loại bỏ biến dị di truyền theo thời gian.^[14]

Tốc độ thay đổi tần số alen do trôi dạt

Mười mô phỏng trôi dạt di truyền ngẫu nhiên của một alen với tần số ban đầu 0.5 trải qua 50 thế hệ, lặp lại trong ba quần thể có kích thước khác nhau sinh sản đồng thời. Trong những mô phỏng này, alen chỉ trôi dạt về biến mất hoặc cố định (tần số 0.0 hoặc 1.0) trong quần thể nhỏ nhất.

Giả sử trôi dạt di truyền là yếu tố tiến hóa duy nhất tác động lên một gen với hai alen với tần số alen ban đầu là p và q. Một cách để đo tốc độ trôi dạt gen là sự giảm biến dạng di truyền thông qua tỉ lệ dị hợp trong quần thể. Nếu tần số dị hợp ban đầu là 2pq theo Hardy–Weinberg, thì tần số dị hợp sau t thế hệ có thể được tính theo công thức:^[15]

${\displaystyle H_{t}=2pq\left(1-{\frac {1}{2N_{e}}}\right)^{t}}$

trong đó N_e là kích thước quần thể hiệu quả. Từ phương trình trên ta thấy tỉ lệ dị hợp giảm khoảng 1 − 1/(2N_e) lần sau mỗi thế hệ, do đó kích thước quần thể hiệu quả càng bé thì tốc độ giảm tính dị hợp càng nhanh.^[16]

Thời gian cố định hoặc biến mất

Giả sử trôi dạt di truyền là nhân tố tiến hóa duy nhất tác động lên alen, ở một thời điểm bất kỳ, xác suất một alen sẽ trở nên cố định bằng tần số của nó trong quần thể vào thời điểm đó.^[17] Ví dụ, nếu tần số p của alen A là 75% và tần số q của alen B là 25%, thì với thời gian vô hạn xác suất A cố định là 75% còn xác suất B cố định là 25%.

Số thế hệ dự kiến cần để xảy ra cố định tỉ lệ thuận với kích thước quần thể, tức cố định được dự đoán là diễn ra nhanh hơn trong quần thể nhỏ hơn.^[18] Thông thường kích thước quần thể hiệu quả được dùng thay cho kích thước quần thể trong việc tính toán những xác suất này, do kích thước quần thể hiệu quả N_e tính tới những yếu tố như giao phối cận huyết, giai đoạn sống mà quần thể là nhỏ nhất, và một số gen trung tính liên kết với những gen khác được chọn lọc.^[19] Kích thước quần thể hiệu quả có thể khác nhau tùy từng gen trong quần thể.^[20]

Theo mô hình Wright-Fisher, một công thức được dùng để xấp xỉ thời gian dự kiến trước khi một alen trung tính cố định bởi trôi dạt di truyền là

${\displaystyle {\bar {t}}_{\text{fix}}={\frac {-4N_{e}(1-p)\ln(1-p)}{p}}}$

trong đó T là số thế hệ, N_e là kích thước quần thể hiệu quả, và p là tần số ban đầu của alen.^[21]

Thời gian dự kiến để một alen trung tính biến mất qua trôi dạt di truyền có thể được tính bằng ^[10]

${\displaystyle {\bar {t}}_{\text{loss}}={\frac {-4N_{e}p\ln p}{1-p}}.}$

Khi biến dị chỉ xuất hiện một lần trong một quần thể lớn khiến tần số ban đầu trở nên không đáng kể, hai công thức trên có thể được thu gọn thành^[22]

${\displaystyle {\bar {t}}_{\text{fix}}=4N_{e}}$

là số thế hệ trung bình trước khi đột biến trung tính cố định, và

${\displaystyle {\bar {t}}_{\text{loss}}=2\left({\frac {N_{e}}{N}}\right)\ln(2N)}$

là số thế hệ trung bình trước khi đột biến trung tính biến mất.^[23]

Thời gian biến mất do trôi dạt và đột biến

Công thức trên áp dụng cho một alen có trong quần thể mà không chịu tác động của đột biến hay chọn lọc tự nhiên. Nếu một alen bị mất nhiều hơn là tạo ra do đột biến thì cả đột biến và trôi dạt đều có thể ảnh hưởng đến thời gian alen biến mất. Nếu một alen chịu ảnh hưởng của đột biến làm mất alen ban đầu cố định trong quần thể, và bị mất bởi đột biến với tốc độ m trên mỗi lần tái bản, thì số thế hệ trung bình cho đến khi nó biến mất trong quần thể đơn bội là

${\displaystyle {\bar {t}}_{\text{lost}}\approx {\begin{cases}{\dfrac {1}{m}},{\text{ }}mN_{e}\ll 1\\[8pt]{\dfrac {\ln {(mN_{e})}+\gamma }{m}}{\text{ }}mN_{e}\gg 1\end{cases}}}$

trong đó ${\displaystyle \gamma }$ là hằng số Euler.^[24] Xấp xỉ thứ nhất biểu diễn thời gian chờ cho đến khi thể đột biến đầu tiên dự kiến biến mất, mất N_e ≪ 1/m. Xấp xỉ thứ hai biểu diễn thời gian cần để biến mất xác định bởi tích lũy đột biến. Trong cả hai trường hợp, thời gian biến mất chịu tác động lớn bởi đột biến qua hệ số 1/m, và ít bị tác độgn bởi kích thước quần thể hiệu quả.

Xem thêm

• Hình thành loài ngoại vi
• Trôi dạt kháng nguyên
• Lý thuyết kết hợp
• Vốn gen
• Phát động giảm phận

Ghi chú và tham khảo

1. Gould SJ (2002). “Chapter 7, section "Synthesis as Hardening"”. The Structure of Evolutionary Theory.
2. Masel J (tháng 10 năm 2011). “Genetic drift”. Current Biology. Cell Press. 21 (20): R837-8. doi:10.1016/j.cub.2011.08.007. PMID 22032182.
3. ^ Futuyma 1998, tr. 320
4. Futuyma 1998, Glossary
5. Star B, Spencer HG (tháng 5 năm 2013). “Effects of genetic drift and gene flow on the selective maintenance of genetic variation”. Genetics. 194 (1): 235–44. doi:10.1534/genetics.113.149781. PMC 3632471. PMID 23457235.
6. Miller 2000, tr. 54
7. Kimura M (tháng 2 năm 1968). “Evolutionary rate at the molecular level”. Nature. Nature Publishing Group. 217 (5129): 624–6. Bibcode:1968Natur.217..624K. doi:10.1038/217624a0. PMID 5637732. S2CID 4161261.
8. “Sampling Error and Evolution”. Understanding Evolution. University of California, Berkeley. Lưu trữ bản gốc ngày 8 tháng 12 năm 2015. Truy cập ngày 1 tháng 12 năm 2015.
9. Wahl LM (tháng 8 năm 2011). “Fixation when N and s vary: classic approaches give elegant new results”. Genetics. Genetics Society of America. 188 (4): 783–5. doi:10.1534/genetics.111.131748. PMC 3176088. PMID 21828279.
10. ^ Hartl & Clark 2007, tr. 112
11. Tian 2008, tr. 11
12. Moran PA (1958). “Random processes in genetics”. Mathematical Proceedings of the Cambridge Philosophical Society. 54 (1): 60–71. Bibcode:1958PCPS...54...60M. doi:10.1017/S0305004100033193.
13. Ewens 2004
14. Li & Graur 1991, tr. 29
15. Hartl, Daniel (2020). A primer of population genetics and genomics. Oxford: Oxford University Press. tr. 154. ISBN 978-0-19-886230-7. OCLC 1187184415.
16. Kliman, R., Sheehy, B. & Schultz, J. (2008) Genetic Drift and Effective Population Size. Nature Education 1(3):3. Truy cập ngày 16 tháng 4 năm 2021 tại Genetic Drift and Effective Population Size
17. Futuyma 1998, tr. 300
18. Otto SP, Whitlock MC (tháng 6 năm 1997). “The probability of fixation in populations of changing size” (PDF). Genetics. Genetics Society of America. 146 (2): 723–33. PMC 1208011. PMID 9178020. Lưu trữ (PDF) bản gốc ngày 19 tháng 3 năm 2015.
19. Charlesworth B (tháng 3 năm 2009). “Fundamental concepts in genetics: effective population size and patterns of molecular evolution and variation”. Nature Reviews. Genetics. Nature Publishing Group. 10 (3): 195–205. doi:10.1038/nrg2526. PMID 19204717. S2CID 205484393.
20. Cutter AD, Choi JY (tháng 8 năm 2010). “Natural selection shapes nucleotide polymorphism across the genome of the nematode Caenorhabditis briggsae”. Genome Research. Cold Spring Harbor Laboratory Press. 20 (8): 1103–11. doi:10.1101/gr.104331.109. PMC 2909573. PMID 20508143.
21. Hedrick 2005, tr. 315
22. Li & Graur 1991, tr. 33
23. Kimura & Ohta 1971
24. Masel J, King OD, Maughan H (tháng 1 năm 2007). “The loss of adaptive plasticity during long periods of environmental stasis”. The American Naturalist. University of Chicago Press on behalf of the American Society of Naturalists. 169 (1): 38–46. doi:10.1086/510212. PMC 1766558. PMID 17206583.

Thư mục

• Avers CJ (1989). Process and Pattern in Evolution. New York: Oxford University Press. ISBN 0-19-505275-7. LCCN 88005368. OCLC 17677554.
• Barton NH, Briggs DE, Eisen JA, Goldstein DB, Patel NH (2007). Evolution. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press. ISBN 978-0-87969-684-9. LCCN 2007010767. OCLC 86090399.
• Campbell NA (1996). Biology. Benjamin/Cummings Series in the Life Sciences (ấn bản thứ 4). Menlo Park, CA: Benjamin/Cummings Pub. Co. ISBN 0-8053-1940-9. LCCN 95045572. OCLC 33333455.
• Cavalli-Sforza LL, Menozzi P, Piazza A (1996). The History and Geography of Human Genes . Princeton, N.J.: Princeton University Press. ISBN 0-691-02905-9. OCLC 35527063.
• Ewens WJ (2004). Mathematical Population Genetics I. Theoretical Introduction. Interdisciplinary Applied Mathematics. 27 (ấn bản thứ 2). New York: Springer-Verlag. ISBN 0-387-20191-2. LCCN 2003065728. OCLC 53231891.
• Freeman S, Herron JC (2007). Evolutionary Analysis (ấn bản thứ 4). Upper Saddle River, NJ: Pearson Prentice Hall. ISBN 978-0-13-227584-2. LCCN 2006034384. OCLC 73502978.
• Futuyma D (1998). Evolutionary Biology (ấn bản thứ 3). Sunderland, MA: Sinauer Associates. ISBN 0-87893-189-9. LCCN 97037947. OCLC 37560100.
• Golding B biên tập (1994). Non-Neutral Evolution: Theories and Molecular Data. New York: Chapman & Hall. ISBN 0-412-05391-8. LCCN 93047006. OCLC 29638235. "Papers from a workshop sponsored by the Canadian Institute for Advanced Research."
• Hartl DL, Clark AG (2007). Principles of Population Genetics (ấn bản thứ 4). Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-308-2. LCCN 2006036153. OCLC 75087956.
• Hedrick PW (2005). Genetics of Populations (ấn bản thứ 3). Boston, MA: Jones and Bartlett Publishers. ISBN 0-7637-4772-6. LCCN 2004056666. OCLC 56194719.
• Hey J, Fitch WM, Ayala FJ biên tập (2005). Systematics and the Origin of Species: On Ernst Mayr's 100th Anniversary. Washington, D.C.: National Academies Press. ISBN 978-0-309-09536-5. LCCN 2005017917. OCLC 70745851.
• Howard DJ, Berlocher SH biên tập (1998). Endless Forms: Species and Speciation. New York: Oxford University Press. ISBN 978-0-19-510901-6. LCCN 97031461. OCLC 37545522.
• Kimura M, Ohta T (1971). Theoretical Aspects of Population Genetics. Monographs in Population Biology. 4. Princeton, NJ: Princeton University Press. tr. 1–219. ISBN 0-691-08096-8. LCCN 75155963. OCLC 299867647. PMID 5162676.
• Larson EJ (2004). Evolution: The Remarkable History of a Scientific Theory. Modern Library Chronicles. 17. New York: Modern Library. ISBN 0-679-64288-9. LCCN 2003064888. OCLC 53483597.
• Li W, Graur D (1991). Fundamentals of Molecular Evolution. Sunderland, MA: Sinauer Associates. ISBN 0-87893-452-9. LCCN 90043581. OCLC 22113526.
• Lynch M (2007). The Origins of Genome Architecture. Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-484-3. LCCN 2007000012. OCLC 77574049.
• Miller G (2000). The Mating Mind: How Sexual Choice Shaped the Evolution of Human Nature. New York: Doubleday. ISBN 0-385-49516-1. LCCN 00022673. OCLC 43648482.
• Sadava D, Heller HC, Orians GH, Purves WK, Hillis DM (2008). Life: The Science of Biology. II: Evolution, Diversity and Ecology (ấn bản thứ 8). Sunderland, MA; Gordonsville, VA: Sinauer Associates; W. H. Freeman and Company. ISBN 978-0-7167-7674-1. LCCN 2006031320. OCLC 71632224.
• Stevenson JC (1991). Dictionary of Concepts in Physical Anthropology. Reference Sources for the Social Sciences and Humanities. 10. Westport, CT: Greenwood Press. ISBN 0-313-24756-0. LCCN 90022815. OCLC 22732327.
• Tian JP (2008). Evolution Algebras and their Applications. Lecture Notes in Mathematics. 1921. Berlin; New York: Springer. doi:10.1007/978-3-540-74284-5. ISBN 978-3-540-74283-8. LCCN 2007933498. OCLC 173807298. Zbl 1136.17001.
• Wolf JB, Brodie ED, Wade MJ biên tập (2000). Epistasis and the Evolutionary Process. Oxford, UK; New York: Oxford University Press. ISBN 0-19-512806-0. LCCN 99046515. OCLC 42603105.
• Zimmer C (2001). Evolution: The Triumph of an Idea. Introduction by Stephen Jay Gould; foreword by Richard Hutton (ấn bản thứ 1). New York: HarperCollins. ISBN 0-06-019906-7. LCCN 2001024077. OCLC 46359440.

Liên kết ngoài

Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Phiêu bạt di truyền.

• Sheehy, Bob. “Population genetics simulation program”. Radford, VA: Radford University. Truy cập ngày 21 tháng 12 năm 2015.
• Grimes, Bill. “Genetic Drift Simulation”. Tucson, Arizona: The University of Arizona. Truy cập ngày 25 tháng 8 năm 2016.