Hình chỏm cầu

Hình chỏm cầu màu xanh và mặt cắt.

Trong hình học không gian, hình chỏm cầu, hình vòm cầu, hay hình đới cầu có một đáy là một phần của hình cầu bị chia bởi một mặt phẳng. Nếu mặt phẳng đi qua tâm của hình cầu, lúc này chiều cao của chỏm cầu bằng bán kính của hình cầu, và hình chỏm cầu thu về một bán cầu.

Thể tích và diện tích bề mặt

Hình chỏm cầu màu xanh (và hình chỏm cầu còn lại có màu đỏ.)

Nếu bán kính của đáy chỏm cầu bằng ${\displaystyle a}$, và chiều cao bằng ${\displaystyle h}$, thì thể tích của hình chỏm cầu bằng^[1]

${\displaystyle V={\frac {\pi h}{6}}(3a^{2}+h^{2})}$

và diện tích phần mặt cong (hay vòm) của chỏm cầu bằng^[1]

${\displaystyle A=2\pi rh}$

hay

${\displaystyle A=2\pi r^{2}(1-\cos \theta )}$

${\displaystyle h}$ và ${\displaystyle r}$ liên hệ với nhau tùy ý sao cho ${\displaystyle 0\leq h\leq 2r}$. Phần màu đỏ cũng được định nghĩa là chỏm cầu.

Các tham số ${\displaystyle a}$, ${\displaystyle h}$ và ${\displaystyle r}$ không độc lập với nhau:

${\displaystyle r^{2}=(r-h)^{2}+a^{2}=r^{2}+h^{2}-2rh+a^{2}}$

${\displaystyle r={\frac {a^{2}+h^{2}}{2h}}}$

Thay thế chúng vào công thức diện tích ở trên thu được:

${\displaystyle A=2\pi {\frac {(a^{2}+h^{2})}{2h}}h=\pi (a^{2}+h^{2})}$.

Đối với chỏm cầu nhỏ ở phía trên, ${\displaystyle h=r-{\sqrt {r^{2}-a^{2}}}}$, và chỏm cầu lớn ở dưới ${\displaystyle h=r+{\sqrt {r^{2}-a^{2}}}}$; và từ đó ${\displaystyle a={\sqrt {h(2r-h)}}}$ thay vào công thức thể tích thu được:

${\displaystyle V={\frac {\pi h^{2}}{3}}(3r-h)}$.

Chứng minh công thức

Phương trình cung sinh của hình chỏm cầu.

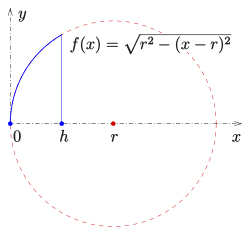
Theo định lý Pythagoras: ${\displaystyle (r-h)^{2}+a^{2}=r^{2}}$. Phá dấu ngoặc và sắp xếp lại:

${\displaystyle 2rh=a^{2}+h^{2}}$.

Thể tích của hình chỏm cầu được tính bằng cách lấy tích phân thể tích hình giới hạn bởi đường cung xoay tròn quanh một trục ${\displaystyle y=f(x)={\sqrt {r^{2}-(x-r)^{2}}}={\sqrt {2rx-x^{2}}}}$:

${\displaystyle V=\pi \int \limits _{0}^{h}f(x)^{2}\,dx=\pi \int \limits _{0}^{h}(2rx-x^{2})\,dx={\frac {\pi h^{2}}{3}}(3r-h)}$.

Tương tự diện tích bề mặt của vòm cầu (không kể đáy) tính bằng tích phân diện tích của mặt tròn xoay

${\displaystyle M=2\pi \int \limits _{0}^{h}f(x)\cdot {\sqrt {1+f'(x)^{2}}}\,dx=2\pi r\int \limits _{0}^{h}\,dx=2\pi rh}$.

Và bao gồm cả đáy: ${\displaystyle O=\pi (2rh+a^{2})=\pi (2a^{2}+h^{2})}$.

Ngoài ra thể tích và diện tích của hình chỏm cầu cũng có thể tính theo góc ${\displaystyle \theta }$:

${\displaystyle V=\int _{r\cos \theta }^{r}\pi \left(r^{2}-x^{2}\right)dx={\frac {\pi }{3}}r^{3}(2-3\cos \theta +\cos ^{3}\theta )={\frac {\pi }{3}}r^{3}(2+\cos \theta )(1-\cos \theta )^{2}}$.

Áp dụng

Thể tích của hợp và giao hai hình cầu

Thể tích của hợp hai hình cầu cắt nhau với bán kính lần lượt ${\displaystyle r_{1}}$ và ${\displaystyle r_{2}}$ là ^[2]

${\displaystyle V=V^{(1)}-V^{(2)}}$,

với

${\displaystyle V^{(1)}={\frac {4\pi }{3}}r_{1}^{3}+{\frac {4\pi }{3}}r_{2}^{3}}$

là tổng thể tích của hai hình cầu riêng rẽ, và

${\displaystyle V^{(2)}={\frac {\pi h_{1}^{2}}{3}}(3r_{1}-h_{1})+{\frac {\pi h_{2}^{2}}{3}}(3r_{2}-h_{2})}$

là tổng thể tích của hai chỏm cầu hình thành bởi đoạn giao giữa hai hình cầu. Nếu ${\displaystyle d<r_{1}+r_{2}}$ là khoảng cách giữa hai tâm hình cầu, bằng cách loại bỏ các biến ${\displaystyle h_{1}}$ và ${\displaystyle h_{2}}$ thu được^[3][4]

${\displaystyle V^{(2)}={\frac {\pi }{12d}}(r_{1}+r_{2}-d)^{2}\left(d^{2}+2d(r_{1}+r_{2})-3(r_{1}-r_{2})^{2}\right)}$ .

Diện tích đường tròn bị chặn bởi các đường tròn vĩ độ

• Xem thêm: Hình đới cầu

Diện tích của bề mặt bị chặn bởi hai đường tròn vĩ độ (hay mặt đới cầu) bằng hiệu số diện tích của hai chỏm cầu tương ứng với hai đường tròn này. Với hình cầu bán kính ${\displaystyle r}$, và cho trước các vĩ độ ${\displaystyle \phi _{1}}$ và ${\displaystyle \phi _{2}}$, diện tích của mặt đới cầu bằng^[5]

${\displaystyle A=2\pi r^{2}|\sin \phi _{1}-\sin \phi _{2}|}$

Ví dụ, giả sử Trái Đất là một hình cầu có bán kính 6371 km, diện tích bề mặt của bắc cực (phía bắc của vòng Bắc Cực, tại vĩ độ 66,56° thời điểm tháng 8 năm 2016^[6]) là 2π·6371²|sin 90° − sin 66.56°| = 21,04 triệu km², hay 0.5·|sin 90° − sin 66.56°| = 4,125% tổng diện tích bề mặt của Trái Đất.

Tổng quát hóa

Tạo thành từ những hình khối khác

Vòm phỏng cầu (spheroidal dome) thu được bằng cách chia một hình phỏng cầu sao cho hình vòm thu được có tính chất đối xứng tròn (circular symmetry) (hay nó có một trục tròn xoay), ví dụ như hình vòm elipsoid nhận được từ ellipsoid.

Siêu chỏm cầu

Tổng quát hơn, thể tích ${\displaystyle n}$-chiều của một siêu chỏm cầu với chiều cao ${\displaystyle h}$ và bán kính ${\displaystyle r}$ trong không gian Euclid ${\displaystyle n}$-chiều cho bởi^[7]

${\displaystyle V={\frac {\pi ^{\frac {n-1}{2}}\,r^{n}}{\,\Gamma \left({\frac {n+1}{2}}\right)}}\int \limits _{0}^{\arccos \left({\frac {r-h}{r}}\right)}\sin ^{n}(t)\,\mathrm {d} t}$

với hàm gamma ${\displaystyle \Gamma }$ cho bởi ${\displaystyle \Gamma (z)=\int _{0}^{\infty }t^{z-1}\mathrm {e} ^{-t}\,\mathrm {d} t}$.

Công thức biểu diễn cho ${\displaystyle V}$ có thể viết dưới dạng thể tích của khối cầu n chiều đơn vị ${\displaystyle C_{n}={\scriptstyle \pi ^{n/2}/\Gamma [1+{\frac {n}{2}}]}}$ và hàm siêu hình học (hypergeometric function) ${\displaystyle {}_{2}F_{1}}$ hoặc hàm beta chính quy hóa không đầy đủ (regularized incomplete beta function) ${\displaystyle I_{x}(a,b)}$ như sau

${\displaystyle V=C_{n}\,r^{n}\left({\frac {1}{2}}\,-\,{\frac {r-h}{r}}\,{\frac {\Gamma [1+{\frac {n}{2}}]}{{\sqrt {\pi }}\,\Gamma [{\frac {n+1}{2}}]}}{\,\,}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1-n}{2}};{\tfrac {3}{2}};\left({\tfrac {r-h}{r}}\right)^{2}\right)\right)={\frac {1}{2}}C_{n}\,r^{n}I_{(2rh-h^{2})/r^{2}}\left({\frac {n+1}{2}},{\frac {1}{2}}\right)}$,

và công thức diện thích ${\displaystyle A}$ có thể biểu diễn theo số hạng của diện tích khối cầu n chiều đơn vị ${\displaystyle A_{n}={\scriptstyle 2\pi ^{n/2}/\Gamma [{\frac {n}{2}}]}}$ như

${\displaystyle A={\frac {1}{2}}A_{n}\,r^{n-1}I_{(2rh-h^{2})/r^{2}}\left({\frac {n-1}{2}},{\frac {1}{2}}\right)}$,

với ${\displaystyle \scriptstyle 0\leq h\leq r}$.

Trước đó trong ^[8] (1986, USSR Academ. Press) công thức sau đã được suy ra: ${\displaystyle A=A_{n}p_{n-2}(q),V=C_{n}p_{n}(q)}$, với ${\displaystyle q=1-h/r(0\leq q\leq 1),p_{n}(q)=(1-G_{n}(q)/G_{n}(1))/2}$,

${\displaystyle G_{n}(q)=\int \limits _{0}^{q}(1-t^{2})^{(n-1)/2}dt}$.

Trường hợp số lẻ ${\displaystyle n=2k+1:}$

${\displaystyle G_{n}(q)=\sum _{i=0}^{k}(-1)^{i}{\binom {k}{i}}{\frac {q^{2i+1}}{2i+1}}}$.

Tiệm cận

Như được chứng minh trong bài báo ^[9] rằng, nếu ${\displaystyle n\to \infty }$ và ${\displaystyle q{\sqrt {n}}={\text{const.}}}$, thì ${\displaystyle p_{n}(q)\to 1-F({q{\sqrt {n}}})}$ với ${\displaystyle F()}$ là tích phân của phân phối chuẩn.

Một cách tính định lượng hơn của biểu diễn trên, như nêu trong ^[10] với giá trị chặn${\displaystyle A/A_{n}=n^{\Theta (1)}\cdot [(2-h/r)h/r]^{n/2}}$ được dẫn ra. Đối với chỏm cầu rất lớn (nghĩa là khi ${\displaystyle (1-h/r)^{4}\cdot n=O(1)}$ khi ${\displaystyle n\to \infty }$), giá trị chặn thu gọn thành ${\displaystyle n^{\Theta (1)}\cdot e^{-(1-h/r)^{2}n/2}}$.

Xem thêm

• Cổng thông tin Toán học

• Hình viên phân (circular segment) — tương tự trong 2 chiều
• Góc khối
• Hình đới cầu (spherical segment)
• Hình quạt cầu (spherical sector)
• Hình chêm cầu (spherical wedge)
• Hình vòng đai cầu trụ (hình giới hạn bởi hình cầu và hình trụ), (spherical ring)

Thảm khảo

1. ^ Polyanin, Andrei D; Manzhirov, Alexander V. (2006), Handbook of Mathematics for Engineers and Scientists, CRC Press, tr. 69, ISBN 9781584885023.
2. Connolly, Michael L. (1985). “Computation of molecular volume”. J. Am. Chem. Soc. 107: 1118–1124. doi:10.1021/ja00291a006.
3. Pavani, R.; Ranghino, G. (1982). “A method to compute the volume of a molecule”. Comput. Chem. 6: 133–135. doi:10.1016/0097-8485(82)80006-5.
4. Bondi, A. (1964). “Van der Waals volumes and radii”. J. Phys. Chem. 68: 441–451. doi:10.1021/j100785a001.
5. Scott E. Donaldson, Stanley G. Siegel. “Successful Software Development”. Truy cập ngày 29 tháng 8 năm 2016.
6. “Obliquity of the Ecliptic (Eps Mean)”. Neoprogrammics.com. Truy cập ngày 13 tháng 5 năm 2014.
7. Li, S (2011). “Concise Formulas for the Area and Volume of a Hyperspherical Cap”. Asian J. Math. Stat. 4 (1): 66–70. doi:10.3923/ajms.2011.66.70.
8. Chudnov, Alexander M. (1986). “On minimax signal generation and reception algorithms (rus.)”. Problems of Information Transmission. 22 (4): 49–54.
9. Chudnov, Alexander M (1991). “Game-theoretical problems of synthesis of signal generation and reception algorithms (rus.)”. Problems of Information Transmission. 27 (3): 57–65.
10. Anja Becker, Léo Ducas, Nicolas Gama, and Thijs Laarhoven. 2016. New directions in nearest neighbor searching with applications to lattice sieving. In Proceedings of the twenty-seventh annual ACM-SIAM symposium on Discrete algorithms (SODA '16), Robert Kraughgamer (Ed.). Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 10-24.

Thư mục

• Richmond, Timothy J. (1984). “Solvent accessible surface area and excluded volume in proteins: Analytical equation for overlapping spheres and implications for the hydrophobic effect”. J. Mol. Biol. 178 (1): 63–89. doi:10.1016/0022-2836(84)90231-6.
• Lustig, Rolf (1986). “Geometry of four hard fused spheres in an arbitrary spatial configuration”. Mol. Phys. 59 (2): 195–207. Bibcode:1986MolPh..59..195L. doi:10.1080/00268978600102011.
• Gibson, K. D.; Scheraga, Harold A. (1987). “Volume of the intersection of three spheres of unequal size: a simplified formula”. J. Phys. Chem. 91 (15): 4121–4122. doi:10.1021/j100299a035.
• Gibson, K. D.; Scheraga, Harold A. (1987). “Exact calculation of the volume and surface area of fused hard-sphere molecules with unequal atomic radii”. Mol. Phys. 62 (5): 1247–1265. Bibcode:1987MolPh..62.1247G. doi:10.1080/00268978700102951.
• Petitjean, Michel (1994). “On the analytical calculation of van der Waals surfaces and volumes: some numerical aspects”. Int. J. Quant. Chem. 15 (5): 507–523. doi:10.1002/jcc.540150504.
• Grant, J. A.; Pickup, B. T. (1995). “A Gaussian description of molecular shape”. J. Phys. Chem. 99 (11): 3503–3510. doi:10.1021/j100011a016.
• Busa, Jan; Dzurina, Jozef; Hayryan, Edik; Hayryan, Shura (2005). “ARVO: A fortran package for computing the solvent accessible surface area and the excluded volume of overlapping spheres via analytic equations”. Comp. Phys. Commun. 165: 59–96. Bibcode:2005CoPhC.165...59B. doi:10.1016/j.cpc.2004.08.002.

Liên kết ngoài

• Weisstein, Eric W., "Spherical cap" từ MathWorld. Derivation and some additional formulas.
• Online calculator for spherical cap volume and area Lưu trữ 2020-07-09 tại Wayback Machine.
• Summary of spherical formulas.