Hàm liên tục
| Một phần của loạt bài về |
| Vi tích phân |
|---|
| Hàm số | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x ↦ f (x) | |||||||||||||||||||||||||||||||||
| Ví dụ theo miền xác định và miền giá trị | |||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| Loại/tính chất | |||||||||||||||||||||||||||||||||
| Hằng · Đồng nhất · Tuyến tính · Đa thức · Hữu tỉ · Đại số · Giải tích · Trơn · Liên tục · Đo được · Đơn ánh · Toàn ánh · Song ánh | |||||||||||||||||||||||||||||||||
| Xây dựng | |||||||||||||||||||||||||||||||||
| Thu hẹp · Hợp · λ · Ngược | |||||||||||||||||||||||||||||||||
| Tổng quát | |||||||||||||||||||||||||||||||||
| Bộ phận · Nhiều giá trị · Ẩn | |||||||||||||||||||||||||||||||||
Trong toán học, một hàm liên tục hay hàm số liên tục là một hàm số không có sự thay đổi đột ngột trong giá trị của nó, gọi là những điểm gián đoạn. Chính xác hơn, thay đổi rất ít đầu vào của hàm liên tục thì sự chênh lệch của đầu ra cũng nhỏ tùy ý. Một hàm số không liên tục còn gọi là hàm gián đoạn. Đến trước thế kỷ 19, các nhà toán học phần lớn sử dụng những khái niệm liên tục cảm tính, dẫn đến những nỗ lực chặt chẽ hóa nó như là định nghĩa epsilon–delta.
Dạng định nghĩa epsilon-delta được đề cập đầu tiên bởi Bernard Bolzano năm 1817. Định nghĩa liên tục ban đầu liên quan đến giới hạn được đưa ra bởi Augustin-Louis Cauchy. Cauchy định nghĩa liên tục của như sau: Một sự tăng vô cùng nhỏ của biến độc lập luôn luôn là một sự thay đổi tăng vô cùng nhỏ của . Cauchy định nghĩa trên một lượng vô cùng nhỏ của biến, định nghĩa của ông ta rất gần với định nghĩa của chúng ta sử dụng ngày nay.
Tính liên tục của hàm số là một khái niệm quan trọng trong tô pô học. Phần mở đầu của bài viết này tập trung vào trường hợp đặc biệt khi đầu vào và đầu ra của hàm số là những số thực. Một dạng mạnh hơn của tính liên tục là liên tục đều. Ngoài ra, bài viết này cũng có định nghĩa cho những trường hợp hàm số giữa hai không gian mêtric. Trong lý thuyết thứ tự, đặc biệt là lý thuyết miền, ta có khái niệm liên tục gọi là tính liên tục Scott.
Định nghĩa chính thức và phân biệt giữa liên tục điểm và liên tục đều được đưa ra đầu tiên bởi Bolzano vào năm 1830 nhưng điều đó không được công bố mãi đến năm 1930. Eduard Heine công bố lần đầu tiên định nghĩa liên tục đều năm 1872, nhưng dựa trên những ý tưởng từ bài giảng của Peter Gustav Lejeune Dirichlet năm 1854.
Một ví dụ đơn giản, hàm số H(t) thể hiện chiều cao của một cây đang mọc tại thời gian t có thể được coi là liên tục. Ngược lại, hàm số M(t) chỉ số tiền trong một tài khoản ngân hàng tại thời gian t là không liên tục, vì nó sẽ "nhảy" mỗi lần một số tiền được gửi vào hay rút ra.
Lịch sử
[sửa | sửa mã nguồn]Dạng định nghĩa epsilon-delta được đề cập đầu tiên bởi Bernard Bolzano năm 1817. Định nghĩa liên tục ban đầu liên quan đến giới hạn được đưa ra bởi Augustin-Louis Cauchy. Cauchy định nghĩa liên tục của như sau: Một sự tăng vô cùng nhỏ của biến độc lập luôn luôn là một sự thay đổi tăng vô cùng nhỏ của . Cauchy định nghĩa trên một lượng vô cùng nhỏ của biến, định nghĩa của ông ta rất gần với định nghĩa của chúng ta sử dụng ngày nay.
Định nghĩa chính thức và phân biệt giữa liên tục điểm và liên tục đều được đưa ra đầu tiên bởi Bolzano vào năm 1830 nhưng điều đó không được công bố mãi đến năm 1930. Eduard Heine công bố lần đầu tiên định nghĩa liên tục đều năm 1872, nhưng dựa trên những ý tưởng từ bài giảng của Peter Gustav Lejeune Dirichlet năm 1854.
Hàm số thực
[sửa | sửa mã nguồn]Định nghĩa
[sửa | sửa mã nguồn]
Một hàm số thực, ở đây nghĩa là hàm số từ tập số thực đến tập số thực, có thể được biểu diễn bằng đồ thị trong mặt phẳng tọa độ; một hàm số như thế là liên tục nếu, nói đại khái, đồ thị của nó là một đường duy nhất không bị đứt gãy chạy trên toàn tập số thực. Một định nghĩa chính xác hơn được đưa ở dưới.[1]
Định nghĩa chặt chẽ cho tính liên tục của hàm số thực thường sử dụng khái niệm giới hạn. Hàm số f theo biến x được gọi là liên tục tại điểm c trên trục số thực nếu giới hạn của f(x) khi x tiến tới c, bằng giá trị f(c); và hàm số được gọi là liên tục nếu nó liên tục tại mọi điểm. Một hàm số được gọi là gián đoạn tại một điểm khi nó không liên tục tại điểm đó. Những điểm này gọi là các điểm gián đoạn.
Có một số cách hiểu khác nhau cho tính liên tục của hàm số. Do đó, khi sử dụng khái niệm liên tục, cần phải cẩn thận coi ý nghĩa liên tục nào được dùng. Khi nói một hàm số là liên tục, người ta có thể mang một trong các ý nghĩa sau:
- Hàm số liên tục tại mọi điểm trong tập xác định của nó. Theo nghĩa này, hàm số f(x) = tan(x) liên tục trên tập xác định là tất cả số thực x ≠ (2n+1)π/2, n số nguyên bất kỳ.
- Tại giá trị biên của tập xác định, chỉ xét giới hạn một bên. Ví dụ, hàm số g(x) = √x, với tập xác định là các số thực không âm, chỉ có giới hạn bên phải tại x = 0. Trong trường hợp này chỉ cần giới hạn một bên của hàm số bằng giá trị của hàm số, tức g có thể coi là liên tục trên toàn bộ tập số thực không âm.
- Hàm số liên tục tại mọi số thực. Theo nghĩa này, hai hàm số nêu trên không liên tục, còn các hàm đa thức, hàm sin, cosin, và hàm mũ đều liên tục.
Sử dụng ký hiệu toán học, có vài cách để định nghĩa hàm liên tục theo một trong ba cách hiểu nói trên.
Đặt f: D ⟶ R là hàm số định nghĩa trên một tập con D của tập số thực R. Tập con D này là tập xác định của f. Một số khả năng cho D bao gồm:
- (D là toàn bộ tập số thực), hoặc với các số thực a, b,
- (D là một khoảng đóng), hay
- (D là một khoảng mở).
Trong trường hợp D là một khoảng mở, a và b không phải là giá trị biên của tập xác định, và các giá trị f(a) và f(b) không ảnh hưởng đến tính liên tục của f trên D.
Định nghĩa liên tục theo giới hạn của hàm
[sửa | sửa mã nguồn]Hàm gọi là liên tục tại điểm trên miền xác định nếu giới hạn của khi tiến dần về tồn tại và bằng giá trị của . Ta viết:
hay chính là 3 điều kiện sau: 1 là xác định tại , 2 là giới hạn bên vế trái là tồn tại, thứ 3 là giá trị của giới hạn phải bằng .
Hàm là liên tục nếu liên tục tại mọi điểm trong miền xác định.
Định nghĩa theo giới hạn của dãy
[sửa | sửa mã nguồn]Cho dãy bất kì trên miền xác định hội tụ về , thì tương ứng dãy hội tụ về

Định nghĩa liên tục theo epsilon–delta
[sửa | sửa mã nguồn]Cho số thực bất kỳ , tồn tại số thực sao cho với mọi trong miền xác định của với , giá trị của thỏa
Liên tục của tại là với mọi , tồn tại sao cho với mọi

Ví dụ
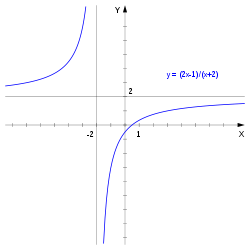
[sửa | sửa mã nguồn]Hàm liên tục trên miền xác định
Phản ví dụ
[sửa | sửa mã nguồn]
Ví dụ về hàm không liên tục với , lấy với mọi , khi đó không tồn tại sao cho vì
Tính chất
[sửa | sửa mã nguồn]Cho là liên tục, giả sử nằm giũa và . Khi đó tồn tại ít nhất một sao cho .
Ví dụ như một đứa trẻ từ khi 4 tuổi đến khi 8 tuổi, chiều cao tăng từ 1m đến 1.5m, khi đó sẽ có 1 thời điểm nào đó trong khoảng 4 tuổi đến 8 tuổi, đứa trẻ cao 1.2m
Định lý giá trị cực biên
[sửa | sửa mã nguồn]Cho khoảng (khoảng đóng và bị chặn) và là liên tục, khi đó có giá trị lớn nhất và giá trị nhỏ nhất trên , hay tồn tại sao cho với mọi .
Định lý điểm cố định
[sửa | sửa mã nguồn]Cho , liên tục, khi đó tồn tại ít nhất một sao cho .
Quan hệ với tính khả tích và khả vi
[sửa | sửa mã nguồn]Mọi hàm khả vi đều liên tục, điều ngược lại không đúng.
Ví dụ hàm trị tuyệt đối
là liên tục trên nhưng không khả vi tại 0.
Đạo hàm của hàm khả vi không nhất thiết phải liên tục, nếu có đạo hàm liên tục thì ta gọi là khải vi liên tục. Tập các hàm này không gian hàm .
Xét tập các hàm
Trong đó là tập con mở trong sao cho hàm khả vi liên tục đến bậc .
Tập các hàm này là không gian .
Mọi hàm
đều khả tích, điều ngược lạ không đúng, ví dụ như hàm

Liên tục đều
[sửa | sửa mã nguồn]Giả sử là tập con của khi đó
liên tục đều trên nếu với mọi cho trước tồn tại chỉ phụ thuộc vào sao cho , thì
Ví dụ như hàm và

Hội tụ của dãy hàm liên tục
[sửa | sửa mã nguồn]Cho dãy
các hàm liên tục sao cho
tồn tại với mọi , khi đó hàm là giới hạn từng điểm của hãy , hàm không nhất thiết liên tục cho dù là liên tục.
Tuy nhiên nếu liên tục, khi đó dãy hội tụ đều
Hàm không liên tục mọi nơi[2]
[sửa | sửa mã nguồn]Là hàm không liên tục tại mọi điểm trên miền xác định. Hàm Dirichlet
Cho và là hai số thực(thường lấy và ), định nghĩa bởi
là không liên tục mọi nơi, hàm có thể phân tích thành
Nếu là tập con bất kì của không gian tô pô sao cho cả và phần bù của trù mật trong sẽ không liên tục mọi nơi. Hàm này được nghiên cứu đầu tiên bởi Peter Gustav Lejeune Dirichlet.[3]
Liên tục trên không gian mêtric
[sửa | sửa mã nguồn]Định nghĩa
[sửa | sửa mã nguồn]Liên tục trên không gian mê tric với định nghĩa:
Cho và là 2 không gian mê tric.
Ánh xạ liên tục tại nếu
hay với mọi tâm tại khi đó tâm tại sao cho
.
Tính chất
[sửa | sửa mã nguồn]- Cho là không gian mêtric, là tập con của thì với là liên tục.
Liên tục Lipchitz[4]
[sửa | sửa mã nguồn]Cho hai không gian mêtric và với là mêtric trên và là mêtric trên .
là liên tục Lipchitz nếu tồn tại hằng số sao cho với mọi
Ví dụ
[sửa | sửa mã nguồn]Hàm liên tục Lipchitz với .
Liên tục Holder[4]
[sửa | sửa mã nguồn]Cho hai không gian mêtric và với là mêtric trên và là mêtric trên , với là số thực.
là liên tục Holder nếu tồn tại hằng số sao cho với mọi
Ví dụ
[sửa | sửa mã nguồn]là liên tục Holder với , nhưng không liên tục Lipchitz.
Liên tục Cauchy[5]
[sửa | sửa mã nguồn]Cho và là hai không gian mêtric, là hàm từ vào .
Hàm là liên tục Cauchy nếu và chỉ nếu cho dãy Cauchy bất kì trong , dãy là dãy Cauchy trong .
Mọi hàm liên tục đều thì liên tục Cauchy, liên tục Cauchy là liên tục. Nếu là không gian đầy đủ, thì mọi hàm liên tục trên là liên tục Cauchy.
ví dụ
[sửa | sửa mã nguồn]Trên đường thẳng thực liên tục cũng chính là liên tục Cauchy.
Hàm khi và khi với mọi số hữu tỉ . Hàm này liên tục trên nhưng không liên tục Cauchy
Liên tục trong không gian tô pô
[sửa | sửa mã nguồn]Nghiên cứu về không gian Tô pô, ta có nhiều khái niệm khác nhau về quan hệ giữa các không gian tô pô với nhau và giữa các không gian con của chúng. Ta muốn xem xét hàm đưa một không gian tô pô vào không gian tô pô khác, Tính liên tục của là một trong những khái niệm cốt lõi của không gian tô pô, được mô tả trực quan tính sinh động trong không gian hình học.
Định nghĩa
[sửa | sửa mã nguồn]
U là lân cận của x trong X
- Cho và là hai không gian tô pô. Ánh xạ là liên tục tại điểm trong nếu mọi tập mở trong chứa thì có tập mở của chứa sao cho chứa trong . Ta nói liên tục trên nếu nó liên tục tại mọi điểm trên .
- Lân cận của điểm là tập con của chứa tập mở chứa . Lân cận không cần phải mở.
- liên tục tại nếu mọi tập mở chứa thì tập là lân cận của .[6]
Định lý
[sửa | sửa mã nguồn]- Ánh xạ là liên tục nếu và chỉ nếu ảnh ngược của tập mở là tập mở. Hay liên tục khi và chỉ khi với mọi mở trong thì mở trong .
- Chứng minh
- () Giả sử rằng là liên tục. Cho là tập mở trong . Cho . Vì liên tục tại và là lân cận mở của thì có mở chứa sao cho chứa trong . Do đó là mở.
- () Giả sử rằng ảnh ngược của mọi tập mở là tập mở. Cho , là lân cận mở của . Khi đó là tập mở chứa , và chứa trong . Vì thế liên tục tại .
Một số tính chất và mệnh đề[7]
[sửa | sửa mã nguồn]- Ánh xạ là liên tục nếu và chỉ nếu ảnh ngược của tập đóng là tập đóng.
- Cho và là hai không gian tô pô và là cơ sở của tô pô trên . Khi đó liên tục nếu và chỉ nếu là mở trong với mọi .
- Cho với tô pô định chuẩn. Khi đó mọi hàm đa thức với là liên tục.
- Giả sử là liên tục. Nếu dãy trong hội tụ về khi đó dãy trong hội tụ về .
- Cho và liên tục. Khi đó hàm hợp là liên tục.
- Cho là hai không gian tô pô, là không gian con của . Cho liên tục. Khi đó liên tục.
Liên tục trong không gian tô pô liên thông[7]
[sửa | sửa mã nguồn]- Cho liên tục, nếu liên thông thì liên thông.
- Cho liên tục, nếu liên thông đường thì liên thông đường.
- Cho là không gian tô pô liên thông, và liên tục. Nếu và , khi đó . (Định lý giá trị trung bình mở rộng)
- Cho liên tục, khi đó tồn tại sao cho .
Liên tục trong không gian tô pô compact[7]
[sửa | sửa mã nguồn]- Cho liên tục, nếu compact thì compact.
- Cho compact và là liên tục, khi đó có giá trị lớn nhất và giá trị nhỏ nhất trên , hay tồn tại sao cho với mọi .
- Cho là khoảng đóng và bị chặn trong . Giả sử là liên tục. Khi đó ảnh của là khoảng đóng và bị chặn trong .


Ví Dụ
[sửa | sửa mã nguồn]- Ví dụ 1: Cho và là 2 không gian tô pô được miêu tả ở hình bên, với xác định:
- Có liên tục và không liên tục.
- Ví dụ 2: Xét với và , có và là hai cơ sở. Ánh xạ
- với biến mỗi phần tử trong thành một phần tử trong là ánh xạ ngược của ánh xạ
- với
- Ánh xạ liên tục.
Xem thêm
[sửa | sửa mã nguồn]Bổ đề dán (The Pasting Lemma)
[sửa | sửa mã nguồn]- Cho là không gian tô pô, là hai tập con đóng của sao cho . Giả sử rẳng và là liên tục và . Khi đó xác định bởi:
thì liên tục trên .
Liên tục thông qua lưới
[sửa | sửa mã nguồn]- Cho là 2 không gian tô pô. Khi đó là liên tục tại nếu và chỉ nếu khi nào có lưới trong hội tụ về , thì lưới hội tụ về .
- Viết theo ký hiệu quen thuộc: liên tục tại nếu và chỉ nếu với mọi lưới .
Liên tục trên không gian tích
[sửa | sửa mã nguồn]- Cho , là tập chỉ số. Khi đó
là liên tục khi và chỉ khi liên tục với mọi thuộc
- Ánh xạ chiếu liên tục.
- Ánh xạ liên tục khi và chỉ khi mỗi ánh xạ thành phần liên tục.
Ví dụ
[sửa | sửa mã nguồn]- Cho hàm , cho bởi:
Mở rộng
[sửa | sửa mã nguồn]Tô pô sinh bởi ánh xạ
[sửa | sửa mã nguồn]- Cho là không gian tô pô, là một tập, và là ánh xạ. Chúng ta muốn tìm tô pô trên sao cho liên tục.
- Yêu cầu của là nếu thì
- Tôpô hiển nhiên (the trivial toplogy)[8] trên thỏa mãn yêu cầu này. Đây là tôpô thô nhất thỏa mãn yêu cầu làm liên tục.
- Mặt khác, họ là tô pô thực sự trên . Đây là tôpô mịn nhất thỏa yêu cầu.
- Cho là một tập, là không gian tô pô, và là ánh xạ. Chúng ta muốn tìm tôpô trên sao cho liên tục.
- Yêu cầu của là nếu thì .
- Tôpô rời rạc trên là tôpô mịn nhất thỏa mãn yêu cầu.
- Ta có thể thấy xa hơn rằng nếu họ sinh ra thì được sinh bởi họ .
Đồng phôi
[sửa | sửa mã nguồn]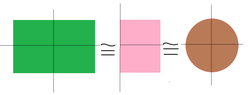
- Ánh xạ đi từ một không gian tôpô vào không gian tôpô khác được gọi là phép đồng phôi nếu nó là song ánh, liên tục và ánh xạ ngược cũng liên tục.
- Hai không gian gọi là đồng phôi, thường viết là , nếu có một phép đồng phôi từ không gian này vào không gian kia.
Đồng luân
[sửa | sửa mã nguồn]
- Định nghĩa: Một biến đổi đồng luân giữa hai ánh xạ liên tục và từ không gian tô pô vào không gian tô pô được định nghĩa là ánh xạ từ tích của không gian với đoạn đơn vị vào sao cho với mỗi thuộc ta có và .
- Nếu ta nghĩ tham số thứ hai của như là "thời gian", khi đó mô tả một biến đổi liên tục ánh xạ thành ánh xạ : tại thời điểm ta có ánh xạ và tại thời điểm ta có ánh xạ .
- Đồng luân là một quan hệ tương đương trên tập các ánh xạ liên tục từ vào . Quan hệ đồng luân này tương thích với phép hợp thành của 2 ánh xạ theo nghĩa nếu là đồng luân và là đồng luân, khi đó hợp thành của chúng và : là đồng luân
Ví dụ
[sửa | sửa mã nguồn]- Ví dụ 1: Cho là ánh xạ biến
- Ta thấy là tô pô mịn nhất sao cho liên tục.
- Ví dụ 2: Mặt phẳng đồng phôi với nửa mặt phẳng và đồng phôi với đĩa tròn
- Ví dụ 3: Một biến đổi đồng luân
Tham khảo
[sửa | sửa mã nguồn]- ^ Speck, Jared (2014). "Continuity and Discontinuity" (PDF). MIT Math. tr. 3. Bản gốc (PDF) lưu trữ ngày 6 tháng 10 năm 2016. Truy cập ngày 2 tháng 9 năm 2016.
Example 5. The function 1/x is continuous on (0, ∞) and on (−∞, 0), i.e., for x > 0 and for x < 0, in other words, at every point in its domain. However, it is not a continuous function since its domain is not an interval. It has a single point of discontinuity, namely x = 0, and it has an infinite discontinuity there.
- ^ Nowhere continuous function - Wikipedia
- ^ Dirichlet Function - from Wolfram MathWorld
- ^ a b Lipschitz continuity - Wikipedia
- ^ Cauchy-continuous function - Wikipedia
- ^ Lecture notes on Topology Lưu trữ ngày 3 tháng 2 năm 2014 tại Wayback Machine, trang 14, HCMUS.
- ^ a b c Introduction to topology pure and applied[liên kết hỏng] của Colin Adam và Robert Franzosa
- ^ The trivial toplogy[liên kết hỏng]
Liên kết ngoài
[sửa | sửa mã nguồn]- Continuity
- Colin Adam và Robert Franzosa Introduction to topology pure and applied
- James Munkres (2000), Topology, Prentice Hall, ISBN 0-13-181629-2
{{Chú thích}}: Liên kết ngoài trong|last= - Gregory L. Naber Topology, Geometry and Gauge fields: Foundations
- Topics in a Topology Coursel
 GIẢM
3%
GIẢM
3%
 GIẢM
13%
GIẢM
13%
![[Review Sách] 7 Định luật giảng dạy](https://down-bs-vn.img.susercontent.com/vn-11134207-7qukw-lidxs3ynamto6c.webp) GIẢM
12%
GIẢM
12%
 GIẢM
31%
GIẢM
31%
 GIẢM
24%
GIẢM
24%
 GIẢM
48%
GIẢM
48%








![{\displaystyle D=[a,b]=\{x\in \mathbf {R} \,|\,a\leq x\leq b\}\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e12e5cf5216c0ab018658e191dcbe91f42ac80d0)






















![{\displaystyle f\,:\,[a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2356fd9d9bd6064f37b5c8a1caafe83a72b5eea2)



![{\displaystyle c\in [a,\,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abed197596791dd5f201e739bb34aa4e630ce8c3)

![{\displaystyle [a,\,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6403d6efced230f17c4b47aaf58879b629b048f)
![{\displaystyle f\,:\,[a,\,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c3c20e6af648c94992a0e3f0507dbdf26fce00b)
![{\displaystyle c,\,d\in [a,\,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ab2f32be2d9ba88e8b4d1ba7872dc8fafcabf28)

![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)

![{\displaystyle f\,:\,[a,\,b]\rightarrow [a,\,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e73f31a7fe062fd3a4f76b68b1a1115e2cb8807b)

















































































































































![{\displaystyle H:\,X\times [0,1]\rightarrow Y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/333160cfd7a2eaa63d1b240451fc8055c3c2281f)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

















